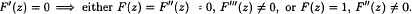Research Article
Average normalisations of elliptic curves
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 353-358
-
- Article
-
- You have access
- Export citation
Smoothing spline in a convex closed set of Hilbert space
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 359-368
-
- Article
-
- You have access
- Export citation
1-perfect codes in Sierpiński graphs
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 369-384
-
- Article
-
- You have access
- Export citation
On boundedness of the weighted Bergman projections on the Lipschitz spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 385-391
-
- Article
-
- You have access
- Export citation
Chapman-Jouguet detonation profile for a qualitative model
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 393-403
-
- Article
-
- You have access
- Export citation
Asymptotical smoothness and its applications
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 405-418
-
- Article
-
- You have access
- Export citation
Most finitely generated subgroups of infinite unitriangular matrices are free
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 419-423
-
- Article
-
- You have access
- Export citation
On totally paranormal operators
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 425-441
-
- Article
-
- You have access
- Export citation
Local well posedness for strongly damped wave equations with critical nonlinearities
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 443-463
-
- Article
-
- You have access
- Export citation
From surfaces in the 5-sphere to 3-manifolds in complex projective 3-space
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 465-475
-
- Article
-
- You have access
- Export citation
Derivations, local derivations and atomic boolean subspace lattices
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 477-486
-
- Article
-
- You have access
- Export citation
C*-algebras of infinite real rank
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 487-496
-
- Article
-
- You have access
- Export citation
There are no denting points in the unit ball of 𝒫(2H)
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 497-498
-
- Article
-
- You have access
- Export citation
Asymptotical well behaviour for constrained minimisation problems
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 499-516
-
- Article
-
- You have access
- Export citation
Existence conditions for a class of modular subgroups of genus zero
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 517-525
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian Ph.D. Theses
Risk factors associated with renal disease in diabetes mellitus
-
- Published online by Cambridge University Press:
- 17 April 2009, p. 527
-
- Article
-
- You have access
- Export citation
Front matter
BAZ volume 66 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
BAZ volume 66 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation

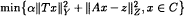 ,
, 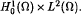 . The space of initial conditions is chosen according to the energy functional, whereas the approach used in this article is based on the theory of analytic semigroups as well as interpolation and extrapolation spaces. This functional analytic framework allows local existence results to be proved in the case of critically growing nonlinearities, which improves the existing results.
. The space of initial conditions is chosen according to the energy functional, whereas the approach used in this article is based on the theory of analytic semigroups as well as interpolation and extrapolation spaces. This functional analytic framework allows local existence results to be proved in the case of critically growing nonlinearities, which improves the existing results.