Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-09T13:33:17.077Z Has data issue: false hasContentIssue false
  • English
  • Français

Local well posedness for strongly damped wave equations with critical nonlinearities

Published online by Cambridge University Press:  17 April 2009

Alexandre N. Carvalho  and
Jan W. Cholewa
Alexandre N. Carvalho
Affiliation:
Departamento de Matemática, Instituto de Ciências Matemáticas e de Computação, Universidade de São Paulo - Campus de São Carlos, Caixa Postal 668, 13.560–970 São Carlos SP, Brazil e-mail: [email protected]
Jan W. Cholewa
Affiliation:
Institute of Mathematics, Silesian University, 40–007 Katowice, Poland e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

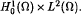In this article the strongly damped wave equation is considered and a local well posedness result is obtained in the product space . The space of initial conditions is chosen according to the energy functional, whereas the approach used in this article is based on the theory of analytic semigroups as well as interpolation and extrapolation spaces. This functional analytic framework allows local existence results to be proved in the case of critically growing nonlinearities, which improves the existing results.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 66 , Issue 3 , December 2002 , pp. 443 - 463
Copyright
Copyright © Australian Mathematical Society 2002

References

[1]Amann, H., Linear and quasilinear parabolic problems (Birkhäuser, Basel, 1995).CrossRefGoogle Scholar
[2]Arietta, J.M. and Carvalho, A.N., ‘Abstract parabolic problems with critical nonlinearities and applications to Navier-Stokes and heat equations’, Trans. Amer. Math. Soc. 352 (2000), 285–310.CrossRefGoogle Scholar
[3]Arietta, J.M., Carvalho, A.N. and Rodriguez-Bernal, A., ‘Parabolic problems with nonlinear boundary conditions and critical nonlinearities’, J. Differential Equations 156 (1999), 376–406.CrossRefGoogle Scholar
[4]Chen, S. and Triggiani, R., ‘Proof of two conjectures of G. Chen and D.L. Russell on structural damping for elastic systems’, in Lecture Notes in Mathematics 1354 (Springer-Verlag, 1988), pp. 234–256.Google Scholar
[5]Chen, S. and Triggiani, R., ‘Proof of extension of two conjectures on structural damping for elastic systems: The case ’, Pacific J. Math. 136 (1989), 15–55.CrossRefGoogle Scholar
[6]Chen, S. and Triggiani, R., ‘Characterization of domains of fractional powers of certain operators arising in elastic systems, and applications’, J. Differential Equations 88 (1990), 279–293.CrossRefGoogle Scholar
[7]Fujita, H. and Kato, T., ‘On the Navier-Stokes initial value problem. I’, Arch. Rational Mech. Anal. 16 (1964), 269–315.CrossRefGoogle Scholar
[8]Kato, T., ‘Fractional powers of dissipative operators II’, J. Math. Soc. Japan 14 (1962), 242–248.CrossRefGoogle Scholar
[9]Triebel, H., Interpolation theory, function spaces, differential operators (Veb Deutscher, Berlin, 1978).Google Scholar