Hostname: page-component-745bb68f8f-hvd4g Total loading time: 0 Render date: 2025-01-22T05:56:01.575Z Has data issue: false hasContentIssue false
  • English
  • Français

Existence conditions for a class of modular subgroups of genus zero

Published online by Cambridge University Press:  17 April 2009

Joachim A. Hempel
Joachim A. Hempel
Affiliation:
School of Mathematics and Statistics, University of Sydney, New South Wales 2006, Australia e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Every subgroup of finite index of the modular group PSL (2, ℤ) has a signature consisting of conjugacy-invariant integer parameters satisfying certain conditions. In the case of genus zero, these parameters also constitute a prescription for the degree and the orders of the poles of a rational function F with the property:

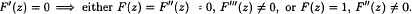
Functions correspond to subgroups, and we use this to establish necessary and sufficient conditions for existence of subgroups with a certain subclass of allowable signatures.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 66 , Issue 3 , December 2002 , pp. 517 - 525
Copyright
Copyright © Australian Mathematical Society 2002

References

[1]Atkin, A.O.L. and Swinnerton-Dyer, H.P.F., ‘Modular forms on noncongruence subgroups’, in Proc. Sympos. Pure Math. 19 (American Mathematical Society, Providence, R.I., 1971), pp. 1–25.Google Scholar
[2]Gunning, R.C., Lectures on modular forms, Annals of Math. Studies 48 (Princeton University Press, Princeton, 1962).CrossRefGoogle Scholar
[3]Hempel, J.A., ‘On the uniformization of the n˜punctured sphere’, Bull. London Math. Soc. 20 (1988), 97–115.CrossRefGoogle Scholar
[4]Hsu, T., ‘Identifying congruence subgroups of the modular group’, Proc. Amer. Math. Soc. 124 (1996), 1351–1359.CrossRefGoogle Scholar
[5]Millington, M.H., ‘Subgroups of the classsical modular group’, J. London Math Soc. 2 1 (1969), 351–357.CrossRefGoogle Scholar
[6]Sebbar, A., ‘Classification of torsion-free genus zero congruence subgroups’, Proc. Amer. Math. Soc. 129 (2001), 2517–2527.CrossRefGoogle Scholar