Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kassem, Mohamed Abd El-Hady
Megahed, Abd El-Monem A.
Arafat, Hebatallah K.
and
Ul-Haq, Wasim
2021.
A Study on Nash-Collative Differential Game of
N
-Players for Counterterrorism.
Journal of Function Spaces,
Vol. 2021,
Issue. ,
p.
1.


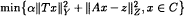 ,
, 