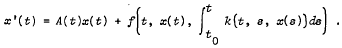Research Article
An embedding theorem for ordered groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 321-335
-
- Article
-
- You have access
- Export citation
On some integrodifferential equations in Banach spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 337-350
-
- Article
-
- You have access
- Export citation
Martin's Axiom and some classical constructions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 351-362
-
- Article
-
- You have access
- Export citation
Secretive prime-power groups of large rank
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 363-369
-
- Article
-
- You have access
- Export citation
On semisubtractive halfrings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 371-378
-
- Article
-
- You have access
- Export citation
A note on a paper of Williamson
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 379-381
-
- Article
-
- You have access
- Export citation
Compatible tight Riesz orders on groups of integer-valued functions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 383-390
-
- Article
-
- You have access
- Export citation
Nonlinear fractional programming
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 391-397
-
- Article
-
- You have access
- Export citation
On a nonlinear elliptic boundary-value problem
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 399-405
-
- Article
-
- You have access
- Export citation
On the problem of non-smoothness of non-reflexive second conjugate spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 407-416
-
- Article
-
- You have access
- Export citation
On the boundedness operator
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 417-423
-
- Article
-
- You have access
- Export citation
Oscillations of an equation relevant to an industrial problem
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 425-431
-
- Article
-
- You have access
- Export citation
Some results on weighing matrices
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 433-447
-
- Article
-
- You have access
- Export citation
Pseudo-distributive near-rings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 449-456
-
- Article
-
- You have access
- Export citation
On Berman's phenomenon in interpolation theory
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 457-465
-
- Article
-
- You have access
- Export citation
Nonlinear eigenvalue problems
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 467-472
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian Ph.D. theses
Processes in the decomposition of networks of queues
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 473-474
-
- Article
-
- You have access
- Export citation
Some investigations of combinatorial integer matrices using cyclotomy
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 475-476
-
- Article
-
- You have access
- Export citation
Unsteady viscous axisymmetric flows associated with rotating surfaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 477-478
-
- Article
-
- You have access
- Export citation
A geometric theory of wild arcs
-
- Published online by Cambridge University Press:
- 17 April 2009, p. 479
-
- Article
-
- You have access
- Export citation