The main result: Let R be a 2-torson free semiprime ring and let D: R → R be a derivation. Suppose that [[D(x), x], x] = 0 holds for all x ∈ R. In this case [D(x), x] = 0 holds for all x ∈ R.

Let A be a hyperplane arrangement in an arbitrary finite dimensional vector space V and let G ≤ GL(V) be an automorphism group of A. If λ is a complex representation of G such that (λ,1)GH=0 for all pointwise isotropy groups GH (H ∈ A), then we prove the “local-global” result that λ does not appear in the representation of G on the Orlik-Solomon algebra of A. The result is applied to complex reflection groups and to finite orthogonal groups. It may also be viewed as a combinatorial result concerning the homology of the lattice of intersections of A. A more general version of the main result is also discussed.

One might think that if the minimal surface equation had a solution on a smooth domain D ⊂ Rn with boundary values φ, it would have a solution with boundary values tφ for all 0 ≤ t ≤ 1. We give a counterexample in R2.

Sufficient conditions are obtained for the existence and global asymptotic stability of a periodic solution in Volterra's population system of integrodifferential equations with periodic coefficients. It is shown that if (i) the intraspecific negative feedbacks are instantaneous and dominate the interspecific effects (ii) the minimum possible growth rates are stronger than the maximum interspecific effects weighted with the respective sizes of all species, when they are near their potential maximum sizes, then the system of integrodifferential equations has a unique componentwise periodic solution which is globally asymptotically stable.

Let H be a complex Hilbert space and let B(H) denote the algebra of all bounded linear operators on H. In this paper we give two necessary and sufficient conditions for an additive bijection of B(H) to be a *-automorphism. Both of the results in the paper are related to the so-called preserver problems.

For any topological near-ring (which is not a ring) whose additive group is the additive group of real numbers, we investigate the near-ring of all continuous functions, under the pointwise operations, from a compact Hausdorff space into that near-ring. Specifically, we determine all the homomorphisms from one such near-ring of functions to another and we show that within a rather extensive class of spaces, the endomorphism semigroup of the near-ring of functions completely determines the topological structure of the space.

We characterise Opial's condition, the non-strict Opial condition, and the uniform Opial condition for a Banach space X in terms of properties of the duality mapping from X into X*.

We prove that varieties of algebras equivalent to Mendelsohn and Steiner quadruple systems can be defined by single identities.

It is shown that two polycyclic-by-finite groups G and H, satisfying the same sentences with one alternation of quantifiers, are commensurable. In fact we show something stronger: given n > 1 there is a subgroup Hn of H and a subgroup Gn of G such that Hn≃G, Gn≃H and the indices [G: Gn] and [H: Hn] are finite and prime to n.

In this paper the structure of finite groups which are the product of two totally permutable subgroups is studied. In fact we can obtain the -residual, where is a formation, -projectors and -normalisers, where is a saturated formation, of the group from the corresponding subgroups of the factor subgroups.

Using the methods of KKM theory, almost fixed point and best approximations theorems in H-spaces are proved.

We characterise reflexive modules over the rings R such that each finitely generated submodule of E(RR) is torsionless (left QF-3″ rings) by means of a suitable linear compactness condition relative to the Lambek torsion theory.

In the case of continuous time systems with bounded operators (coefficients) the following result, of Perron type is well known: “The linear differential system ẋ = Ax + f(t) has, for every function f continuous and bounded on ℝ, a unique bounded solution on ℝ, if and only if the spectrum of the operator A has no points on the imaginary axis”.

We obtain an inequality concerning the width and diameter of a planar convex set with interior containing no point of the rectangular lattice. We then use the result to obtain a corresponding inequality for a planar convex set with interior containing exactly two points of the integral lattice.

Recently J. Miao proved that if is a holomorphic function with Hadamard gaps on the open unit disc D then f ∈ Xp if and only if f ∈ Bp if and only if if and if only if where Xp, Bp and denote respectively the class of holomorphic functions on D which satisfy |f′(z)|p(1 − |z|2)p − 1dxdy is a finite measure, a Carleson measure and a little Carleson measure on D. In this paper we give a higher-dimensional version of Miao's result.

Consider the singular boundary value problem (r(x′))′ + f(t, x) = 0, 0 < t < 1. We give necessary and sufficient conditions for this problem to have solutions. In addition, a uniqueness result is obtained.

Let K1 and K2 be extension fields over a field K with char K = p > 0. Assume L = K1(x1) = K2(x2) ⊃ K where xi is transcendental over Ki, for i = 1, 2. In this paper we prove that if K1 is a perfect field, then K1 = K2.

Strong solvability and uniqueness in the Sobolev space W2, q(Ω), q > n, are proved for the oblique derivative problem

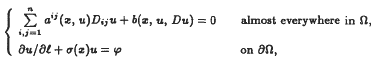
assuming the coefficients of the quasilinear elliptic operator to be Carathéodory functions, aij ∈ VMO∩L∞ with respect to x, and b to grow at most quadratically with respect to the gradient.

The study of nonclassical solutions for elliptic and parabolic PDE's often involves the use of regularisation processes such as the sup- and inf-convolutions. In this note we study the behaviour of these regularised functions near the boundary of the domain, and derive constraints on the appropriate second-order sub- and superdifferentials on and near the boundary. Potential applications to regularity results are also noted.