Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-16T15:24:15.529Z Has data issue: false hasContentIssue false
  • English
  • Français

A property of series of holomorphic homogeneous polynomials with Hadamard gaps

Published online by Cambridge University Press:  17 April 2009

Jun Soo Choa
Jun Soo Choa
Affiliation:
Department of Mathematics EducationSung Kyun Kwan UniversityJongro–GuSeoul 110-745Korea e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Recently J. Miao proved that if 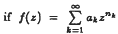is a holomorphic function with Hadamard gaps on the open unit disc D then f ∈ Xp if and only if f ∈ Bp if and only if 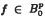if and if only if 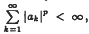where Xp, Bp and 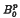denote respectively the class of holomorphic functions on D which satisfy |f′(z)|p(1 − |z|2)p − 1dxdy is a finite measure, a Carleson measure and a little Carleson measure on D. In this paper we give a higher-dimensional version of Miao's result.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 53 , Issue 3 , June 1996 , pp. 479 - 484
Copyright
Copyright © Australian Mathematical Society 1996

References

[1]Choa, J.S., ‘Some properies of analytic functions on the unit ball with Hadamard gaps’, Complex Variables Theory Appl. (to appear).Google Scholar
[2]Garnett, J.B., Bounded analytic functions (Academic Press, New York, 1981).Google Scholar
[3]Hallenbeck, D.J. and Samotij, K., ‘On radial variation of bounded analytic funcions’, Complex Variables Theory Appl. 15 (1990), 43–52.Google Scholar
[4]Jevtić, M., ‘On the Carleson measure characterization of BMOA functions on the unit ball’, Proc. Amer. Math. Soc. 114 (1992), 379–386.CrossRefGoogle Scholar
[5]Mateljević, M. and Pavlović, M., ‘L p-behavior of power series with positive coefficients and Hardy spaces’, Proc. Amer. Math. Soc. 87 (1983), 309–316.Google Scholar
[6]Miao, J., ‘A property of analytic functions with Hadamard gaps’, Bull. Austral. Math. Soc. 45 (1992), 105–112.CrossRefGoogle Scholar
[7]Ryll, J. and Wojtaszczyk, P., ‘On homogeneous polynomials on a complex ball’, Trans. Amer. Math. Soc. 276 (1983), 107–116.CrossRefGoogle Scholar
[8]Rudin, W., Function theory in the unit ball of Cn (Springer-Verlag, Berlin, Heidelberg, New York, 1980).CrossRefGoogle Scholar
[9]Stanton, C.S., ‘Counting functions and majorization for Jensen measures’, Pacific J. Math. 125 (1986), 459–468.CrossRefGoogle Scholar
[10]Ullrich, D., ‘Radial divergence in BMOA’, Proc. London Math. Soc. 68 (1994), 145–160.CrossRefGoogle Scholar