In this note 4-fold torsion theories (for categories of modules) are classified by means of orthogonal pairs of comaximal ideals. Among the applications are results of Kurata concerning lengths of n-fold torsion theories and an upper bound for the number of 4-fold torsion theories over a semiperfect ring.

The third order delay equation

y‴(t) + a(t)yτ(t) = 0

is studied for its nonoscillatory nature under the general condition in which a(t) has been allowed to oscillate. It is shown by way of a differential inequality that if g(t) is a thrice differentiable and eventually positive function then

g‴(t) + t2|a(t)|g(t) ≤ 0

is sufficient for this equation to have bounded nonoscillatory solutions.

Let V = mk + 1 be a prime power; we show for m even it is not possible to partition the Galois field GF(v) to give four (0, 1, −1) matrices X1, X2, X3, X4 satisfying:

(i) Xi * Xj = 0, i ≠ j, i, j = 1, 2, 3, 4;

(ii) 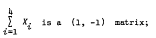is a (1, −1) matrix;

(iii) 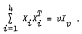Thus this method of partitioning the Galois field GF(V), into four matrices satisfying the above conditions, cannot be used to find Baumert-Hall Hadamard arrays BH[4V] for v = 9, 11, 17, 23, 27, 29, ….

A star is a connected graph in which every vertex but one has valency 1. This paper concerns the question of when complete graphs can be decomposed into stars, all of the same order, which have pairwise disjoint edge-sets. It is shown that the complete graphs on rm and rm + 1 vertices, r > 1, can be decomposed into stars with m edges, if and only if r is even or m is odd.

Let X be a reflexive Banach space and be a family of weakly continuous operators which map X to X. Conditions are provided which guarantee the existence and the uniqueness to the Cauchy initial value problem

An ordinary second order differential equation is considered in which the coefficients are dependent on two parameters ω and F as well as the independent variable μ. The equation arises in the study of free oscillations of incompressible inviscid fluid in global shells. An asymptotic technique is presented which estimates the eigenvaiues (that is the values of ω for which the solution is bounded for all |μ| ≤ 1) as functions of F, as F → ∞. The agreement of the results with numerical computations is also discussed.

Majorant functions for contractors can be defined in a natural war. Such a case is considered here in order to find iterative solutions of general equations in Banach spaces by means of contractors. A class of majorant functions is defined which contains in particular the linear majorant ones. Local and global existence and convergence theorems are proved.

If f is a p–th integrable function on the circle group and ω(p; f; δ) is its mean modulus of continuity with exponent p then an extended version of the classical theorem of Jackson states the for each positive integer n, there exists a trigonometric polynomial tn of degree at most n for which

‖f-tn‖p ≤(p; f; 1/n).

In this paper it will be shewn that for G a Hausdorff locally compact abelian group, the algebra L1(G) admits a certain bounded positive approximate unit which, in turn, will be used to prove an analogue of the above result for Lp(G).

It is shown that for arbitrary countable dense ssets A and B of the real line, there exists a transcendental entire function whose restriction to the real line is a real-valued strictly monotone increasing surjection taking A onto B The technique used is a modification of the procedure Maurer used to show that for countable dense subsets A and B of the plane, there exists a transcendental entire function whose restriction to A is a bijection from A to B.

Let M be a connected C∞. A method is being introduced here to study the action of the holonomy group and the restricted holonomy group of Γ on a recurrent tensor. The main result of this paper is that if the recurrence covector W of a recurrent tensor S on M is an exact form then the tensor S is invariant under the holonomy group of Γ and if W is a closed form then S is invariant under the restricted holonomy group of Γ. In the last section, this result is applied to some particular cases including the case of a riemannian manifold with recurrent curvature.

A graph X is edge-reconstructible if it is uniquely determined up to isomorphism by the set of graphs X – e obtained by deleting one, edge e. The graphs of a comparatively rich class are shown to be edge-reconstructible. This class contains all non-trivial strong products and certain lexicographic products.

This paper presents a two-variable basis for the variety generated by the finite simple group PSL(2, 2n).

A proof is given of a result deduced from numerical work on the conformal mapping of the region exterior to a quadrilateral possessing an axis of symmetry. It is shown that the result follows from known relationships between hypergeometric functions.

In this note we give details of a method by which we can produce an index-0 graph from any unstable graph and use it to show that given any finite group there exists an index-0 graph whose automorphism group is isomorphic, as an abstract group, to the given group. We proceed to construct two infinite families of connected index-0 graphs with connected complements whose automorphism group contains a transposition. This enables us to produce, for any finite group G, an index-0 graph whose automorphism group, isomorphic as an abstract group to C2 × G, contains a transposition.

Let R be a commutative ring with identity. We say that tor is associative over R if for all R-modules A, B, C there is an isomorphism Our main results are that (1) tor is associative over a noetherian ring R if and only if R is the direct sum of a finite number of Dedekind rings and uniserial rings, and (2) tor is associative over an integral domain R if and only if R is a Prüfer ring.

A weighing matrix is an n × n matrix W = W(n, k) with entries from {0, 1, −1}, satisfying = WWt = KIn. We shall call k the degree of W. It has been conjectured that if n ≡ 0 (mod 4) then there exist n × n weighing matrices of every degree k ≤ n.

We prove the conjecture when n is a power of 2. If n is not a power of two we find an integer t < n for which there are weighing matrices of every degree ≤ t.

An unsolved problem in discrete analytic function theory has been to find a suitable analogue of the function . An analogue z(α), of the function zα, is found here for discrete analytic functions of the first kind (or monodiffric functions). This function resolves a conjecture of Isaacs in the negative, and at the same time it introduces multi-valued functions into the discrete analytic theory.

The largest group of exponent 4 generated by n elements of order 2 has nilpotency class n + 1 when n ≥ 3.