Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Cooper, Joan
1975.
Some investigations of combinatorial integer matrices using cyclotomy.
Bulletin of the Australian Mathematical Society,
Vol. 12,
Issue. 3,
p.
475.
Cooper, Joan
and
Wallis, Jennifer Seberry
1976.
Using cyclotomy to construct orthogonal designs.
Journal of the Australian Mathematical Society,
Vol. 22,
Issue. 1,
p.
119.
Agaian, S. S.
and
Sarukhanian, A. G.
1978.
Current Topics in Cybernetics and Systems.
p.
35.
Behn, Daniel
2007.
The Effect of Dual Pricing Practices on Trade, the Environment, and Economic Development: Identifying the Winners and the Losers Under the Current WTO Disciplines.
SSRN Electronic Journal,


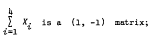 is a (1, −1) matrix;
is a (1, −1) matrix;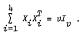 Thus this method of partitioning the Galois field GF(V), into four matrices satisfying the above conditions, cannot be used to find Baumert-Hall Hadamard arrays BH[4
Thus this method of partitioning the Galois field GF(V), into four matrices satisfying the above conditions, cannot be used to find Baumert-Hall Hadamard arrays BH[4