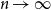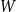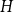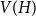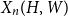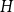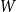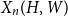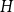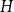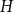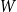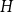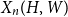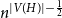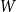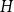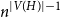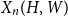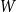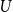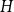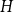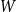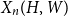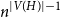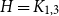We use Stein’s method to obtain distributional approximations of subgraph counts in the uniform attachment model or random directed acyclic graph; we provide also estimates of rates of convergence. In particular, we give uni- and multi-variate Poisson approximations to the counts of cycles and normal approximations to the counts of unicyclic subgraphs; we also give a partial result for the counts of trees. We further find a class of multicyclic graphs whose subgraph counts are a.s. bounded as $n\to \infty$.

This paper investigates properties of the class of graphs based on exchangeable point processes. We provide asymptotic expressions for the number of edges, number of nodes, and degree distributions, identifying four regimes: (i) a dense regime, (ii) a sparse, almost dense regime, (iii) a sparse regime with power-law behaviour, and (iv) an almost extremely sparse regime. We show that, under mild assumptions, both the global and local clustering coefficients converge to constants which may or may not be the same. We also derive a central limit theorem for subgraph counts and for the number of nodes. Finally, we propose a class of models within this framework where one can separately control the latent structure and the global sparsity/power-law properties of the graph.

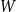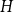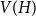Given a graphon $W$ and a finite simple graph $H$ , with vertex set $V(H)$ , denote by 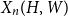$X_n(H, W)$ the number of copies of 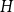$H$ in a 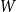$W$ -random graph on $n$ vertices. The asymptotic distribution of 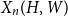$X_n(H, W)$ was recently obtained by Hladký, Pelekis, and Šileikis [17] in the case where 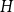$H$ is a clique. In this paper, we extend this result to any fixed graph 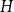$H$ . Towards this we introduce a notion of 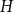$H$ -regularity of graphons and show that if the graphon 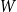$W$ is not 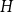$H$ -regular, then 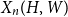$X_n(H, W)$ has Gaussian fluctuations with scaling 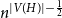$n^{|V(H)|-\frac{1}{2}}$ . On the other hand, if 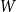$W$ is 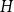$H$ -regular, then the fluctuations are of order 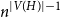$n^{|V(H)|-1}$ and the limiting distribution of 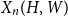$X_n(H, W)$ can have both Gaussian and non-Gaussian components, where the non-Gaussian component is a (possibly) infinite weighted sum of centred chi-squared random variables with the weights determined by the spectral properties of a graphon derived from 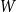$W$ . Our proofs use the asymptotic theory of generalised 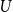$U$ -statistics developed by Janson and Nowicki [22]. We also investigate the structure of 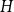$H$ -regular graphons for which either the Gaussian or the non-Gaussian component of the limiting distribution (but not both) is degenerate. 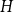Interestingly, there are also $H$ -regular graphons 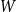$W$ for which both the Gaussian or the non-Gaussian components are degenerate, that is, 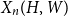$X_n(H, W)$ has a degenerate limit even under the scaling 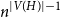$n^{|V(H)|-1}$ . We give an example of this degeneracy with 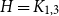$H=K_{1, 3}$ (the 3-star) and also establish non-degeneracy in a few examples. This naturally leads to interesting open questions on higher order degeneracies.

We bound the error for the normal approximation of the number of triangles in the Erdős–Rényi random graph with respect to the Kolmogorov metric. Our bounds match the best available Wasserstein bounds obtained by Barbour et al. [(1989). A central limit theorem for decomposable random variables with applications to random graphs. Journal of Combinatorial Theory, Series B 47: 125–145], resolving a long-standing open problem. The proofs are based on a new variant of the Stein–Tikhomirov method—a combination of Stein's method and characteristic functions introduced by Tikhomirov [(1976). The rate of convergence in the central limit theorem for weakly dependent variables. Vestnik Leningradskogo Universiteta 158–159, 166].

Various types of graph statistics for graphs and digraphs are presented as numerators of incomplete U-statistics, with symmetric and asymmetric kernels, respectively. Thus, asymptotic Poisson limits of these statistics are provided by using limit theorems for the sums of dissociated random variables. Several applications to statistical analysis of graphs are given.