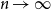1. Introduction
A random uniform attachment graph, denoted
![]() $G^m_n$
and also known as a uniform random recursive dag (directed acyclic graph), can be constructed recursively as follows. Fix
$G^m_n$
and also known as a uniform random recursive dag (directed acyclic graph), can be constructed recursively as follows. Fix
![]() $m\geqslant 1$
. The initial graph
$m\geqslant 1$
. The initial graph
![]() $G^m_1$
is a single isolated vertex. To construct
$G^m_1$
is a single isolated vertex. To construct
![]() $G^m_{n}$
from
$G^m_{n}$
from
![]() $G^m_{n-1}$
, we add vertex
$G^m_{n-1}$
, we add vertex
![]() $n$
to
$n$
to
![]() $G^m_{n-1}$
, with vertex
$G^m_{n-1}$
, with vertex
![]() $n$
born with
$n$
born with
![]() $m$
edges, which are labelled by
$m$
edges, which are labelled by
![]() $1,\dots, m$
. For
$1,\dots, m$
. For
![]() $i\in [m]\,:\!=\,{\{1,\dots, m\}}$
, the other endpoint of
$i\in [m]\,:\!=\,{\{1,\dots, m\}}$
, the other endpoint of
![]() $n^{(i)}$
, the
$n^{(i)}$
, the
![]() $i$
th edge of vertex
$i$
th edge of vertex
![]() $n$
, is then uniformly chosen among the existing vertices of
$n$
, is then uniformly chosen among the existing vertices of
![]() $G^m_{n-1}$
, i.e., in
$G^m_{n-1}$
, i.e., in
![]() $[n-1]$
. Thus,
$[n-1]$
. Thus,
![]() $G^m_n$
has
$G^m_n$
has
![]() $n$
vertices and
$n$
vertices and
![]() $(n-1)m$
edges, and each edge has a label in
$(n-1)m$
edges, and each edge has a label in
![]() $[m]$
. Observe that we allow multiple edges when
$[m]$
. Observe that we allow multiple edges when
![]() $m\geqslant 2$
. An edge in
$m\geqslant 2$
. An edge in
![]() $G^m_n$
can be thought of as always pointing towards the vertex with the smaller label, and so there is no real distinction between the undirected and directed versions of the uniform attachment graph.
$G^m_n$
can be thought of as always pointing towards the vertex with the smaller label, and so there is no real distinction between the undirected and directed versions of the uniform attachment graph.
When
![]() $m=1$
, the model is the random recursive tree first studied in [Reference Na and Rapoport16]; and when
$m=1$
, the model is the random recursive tree first studied in [Reference Na and Rapoport16]; and when
![]() $m\geqslant 2$
, the model was first introduced in [Reference Devroye and Lu6]. There is an abundance of literature on random recursive trees (see e.g. [Reference Drmota7] for an overview), but here we mention [Reference Feng and Mahmoud9–Reference Fuchs11, Reference Holmgren and Janson13], which provide Poisson and normal approximations to the counts of subtree copies. For
$m\geqslant 2$
, the model was first introduced in [Reference Devroye and Lu6]. There is an abundance of literature on random recursive trees (see e.g. [Reference Drmota7] for an overview), but here we mention [Reference Feng and Mahmoud9–Reference Fuchs11, Reference Holmgren and Janson13], which provide Poisson and normal approximations to the counts of subtree copies. For
![]() $m\geqslant 2$
, results on vertex degrees can be found in [Reference Devroye and Lu6, Reference Tsukiji and Mahmoud18], and results on depths and path lengths are available in [Reference Arya, Golin and Mehlhorn1, Reference Broutin and Fawzi3, Reference Devroye and Janson5, Reference Tsukiji and Xhafa19]. The recent paper [Reference Janson14] studies the number of vertices that can be reached from vertex
$m\geqslant 2$
, results on vertex degrees can be found in [Reference Devroye and Lu6, Reference Tsukiji and Mahmoud18], and results on depths and path lengths are available in [Reference Arya, Golin and Mehlhorn1, Reference Broutin and Fawzi3, Reference Devroye and Janson5, Reference Tsukiji and Xhafa19]. The recent paper [Reference Janson14] studies the number of vertices that can be reached from vertex
![]() $n$
via a directed path, where the edge is thought as pointing from the larger vertex label towards the smaller one.
$n$
via a directed path, where the edge is thought as pointing from the larger vertex label towards the smaller one.
In this article, we consider the counts of subgraphs of
![]() $G^m_n$
isomorphic to a given fixed graph as
$G^m_n$
isomorphic to a given fixed graph as
![]() $n\to \infty$
, where the parameter
$n\to \infty$
, where the parameter
![]() $m$
is fixed with
$m$
is fixed with
![]() $m\ge 2$
(Figure 1). We provide uni- and multivariate Poisson approximations to the counts of cycles. We also prove that the counts of unicyclic subgraphs are asymptotically normal (after suitable renormalisation). We conjecture that the counts of more general trees are approximately normal and show that this conjecture holds for stars. All these approximation results are accompanied with convergence rates. We also consider multicyclic subgraphs. In particular, we show that if in addition to having more than two cycles, the subgraph is ‘leaf-free’ (i.e. has no vertices of degree one), then the number of copies in the uniform attachment graph is bounded a.s. For multicyclic subgraphs that are not leaf-free, we identify the exact rate of growth of the expectation and an upper bound on the variance. We conjecture that the count of a subgraph of this type converges a.s. after suitable rescaling, and prove a special case.
$m\ge 2$
(Figure 1). We provide uni- and multivariate Poisson approximations to the counts of cycles. We also prove that the counts of unicyclic subgraphs are asymptotically normal (after suitable renormalisation). We conjecture that the counts of more general trees are approximately normal and show that this conjecture holds for stars. All these approximation results are accompanied with convergence rates. We also consider multicyclic subgraphs. In particular, we show that if in addition to having more than two cycles, the subgraph is ‘leaf-free’ (i.e. has no vertices of degree one), then the number of copies in the uniform attachment graph is bounded a.s. For multicyclic subgraphs that are not leaf-free, we identify the exact rate of growth of the expectation and an upper bound on the variance. We conjecture that the count of a subgraph of this type converges a.s. after suitable rescaling, and prove a special case.

Figure 1. A 4-cycle (with blue and dotted edges) as a subgraph of
![]() $G_5^2$
.
$G_5^2$
.
The distributional approximation tool that we use here is Stein’s method, using in particular the size-bias coupling for both types of approximations; see [Reference Barbour, Holst and Janson2, Reference Chen, Goldstein and Shao4, Reference Ross17] for an overview. This is in contrast to the analytic and contraction methods employed in [Reference Feng and Mahmoud9–Reference Fuchs11]. In [Reference Holmgren and Janson13], Stein’s method was applied in proving the Poisson and normal approximation results for the counts of subgraphs and their functionals in random recursive trees. However, we note that, for normal approximation, the approach that we use here is different from that in [Reference Holmgren and Janson13], which does not provide a convergence rate.
A major challenge in the distributional approximation problem of subgraph counts in the uniform attachment graph is the computation of the variance of the counts. In particular, our methods require a lower bound on the variance. In the case
![]() $m=1$
, the variance can be computed explicitly by using an elegant bijection between the random binary tree and the random recursive tree [ [Reference Knuth15], Section 2.3.2], as done in [Reference Holmgren and Janson13]. When
$m=1$
, the variance can be computed explicitly by using an elegant bijection between the random binary tree and the random recursive tree [ [Reference Knuth15], Section 2.3.2], as done in [Reference Holmgren and Janson13]. When
![]() $m\geqslant 2$
, the order of the variance of the count of certain non-tree subgraphs can be obtained by analysing the covariances of the indicators that a certain subgraph exists in
$m\geqslant 2$
, the order of the variance of the count of certain non-tree subgraphs can be obtained by analysing the covariances of the indicators that a certain subgraph exists in
![]() $G^m_n$
, and finding the pairs of subgraphs that contribute the dominant term in the variance, but this task becomes difficult in the case of trees. In contrast to the case of
$G^m_n$
, and finding the pairs of subgraphs that contribute the dominant term in the variance, but this task becomes difficult in the case of trees. In contrast to the case of
![]() $m=1$
, it is also much harder to obtain an explicit expression for the mean and variances in the case of
$m=1$
, it is also much harder to obtain an explicit expression for the mean and variances in the case of
![]() $m\geqslant 2$
. This is due to the fact for most subgraphs, the same set of vertices in the uniform attachment graph can form a copy in several ways. Consequently, we are only able to give the order of the mean and variance (i.e., within constant factors), and in some cases only an upper bound, and we only consider fixed subgraphs and a fixed
$m\geqslant 2$
. This is due to the fact for most subgraphs, the same set of vertices in the uniform attachment graph can form a copy in several ways. Consequently, we are only able to give the order of the mean and variance (i.e., within constant factors), and in some cases only an upper bound, and we only consider fixed subgraphs and a fixed
![]() $m$
.
$m$
.
Remark 1.1. It would be interesting to extend the results of this paper to subgraphs
![]() $H_n$
depending on
$H_n$
depending on
![]() $n$
, or to
$n$
, or to
![]() $m=m(n)$
growing with
$m=m(n)$
growing with
![]() $n$
. Our methods still work in principle, but it becomes more complicated to estimate the various expressions, and we have not pursued this. We leave these as open problems.
$n$
. Our methods still work in principle, but it becomes more complicated to estimate the various expressions, and we have not pursued this. We leave these as open problems.
2. Notation
The objective of this paper is thus to study the number of copies of a given graph
![]() $H$
in
$H$
in
![]() $G^m_n$
. We will only consider connected
$G^m_n$
. We will only consider connected
![]() $H$
. We emphasise that we generally see both
$H$
. We emphasise that we generally see both
![]() $G^m_n$
and the
$G^m_n$
and the
![]() $H$
as undirected. However, each edge in
$H$
as undirected. However, each edge in
![]() $G^m_n$
has a canonical direction where an edge between the vertices
$G^m_n$
has a canonical direction where an edge between the vertices
![]() $i$
and
$i$
and
![]() $j$
is directed towards the smaller of
$j$
is directed towards the smaller of
![]() $i$
and
$i$
and
![]() $j$
. Thus every copy of
$j$
. Thus every copy of
![]() $H$
in
$H$
in
![]() $G^m_n$
also has an induced direction on its edges. Note, however, that different copies may induce different directions in
$G^m_n$
also has an induced direction on its edges. Note, however, that different copies may induce different directions in
![]() $H$
.
$H$
.
Let
![]() $K^m_n$
be the
$K^m_n$
be the
![]() $m$
-fold complete multigraph on
$m$
-fold complete multigraph on
![]() $n$
, defined to be the multigraph on
$n$
, defined to be the multigraph on
![]() $[n]$
such that for every pair
$[n]$
such that for every pair
![]() $(i,j)$
with
$(i,j)$
with
![]() $1\leqslant i\lt j\leqslant n$
, there are
$1\leqslant i\lt j\leqslant n$
, there are
![]() $m$
edges
$m$
edges
![]() $j\to i$
, and these edges are labelled
$j\to i$
, and these edges are labelled
![]() $1,\dots, m$
. We denote the edge
$1,\dots, m$
. We denote the edge
![]() $j\to i$
with label
$j\to i$
with label
![]() $a$
by
$a$
by
![]() $ji^{(a)}$
. Note that we can regard
$ji^{(a)}$
. Note that we can regard
![]() $G^m_n$
as a subgraph of
$G^m_n$
as a subgraph of
![]() $K^m_n$
in the obvious way (preserving edge labels); in fact, we may define
$K^m_n$
in the obvious way (preserving edge labels); in fact, we may define
![]() $G^m_n$
as the subgraph of
$G^m_n$
as the subgraph of
![]() $K^m_n$
obtained by choosing, for every
$K^m_n$
obtained by choosing, for every
![]() $j\in \{2,\dots, n\}$
and every
$j\in \{2,\dots, n\}$
and every
![]() $a\in [m]$
, exactly one of the edges
$a\in [m]$
, exactly one of the edges
![]() $ji^{(a)}$
with label
$ji^{(a)}$
with label
![]() $a$
and
$a$
and
![]() $i\in [j-1]$
, all choices uniformly at random and independent.
$i\in [j-1]$
, all choices uniformly at random and independent.
Let
![]() $\Gamma$
be the set of all copies of
$\Gamma$
be the set of all copies of
![]() $H$
in
$H$
in
![]() $K^m_n$
that do not contain two different edges
$K^m_n$
that do not contain two different edges
![]() $ji_1^{(a)}$
and
$ji_1^{(a)}$
and
![]() $ji_2^{(a)}$
with
$ji_2^{(a)}$
with
![]() $i_1,i_2\lt j$
and the same label
$i_1,i_2\lt j$
and the same label
![]() $a$
. (If there are two such edges
$a$
. (If there are two such edges
![]() $ji_1^{(a)}$
and
$ji_1^{(a)}$
and
![]() $ji_2^{(a)}$
, then the copy can never be a subgraph of
$ji_2^{(a)}$
, then the copy can never be a subgraph of
![]() $G^m_n$
.) We say that
$G^m_n$
.) We say that
![]() $\Gamma$
is the set of potential copies of
$\Gamma$
is the set of potential copies of
![]() $H$
in
$H$
in
![]() $G^m_n$
. For
$G^m_n$
. For
![]() $\alpha \in \Gamma$
, let
$\alpha \in \Gamma$
, let
![]() ${\mathbf{1}}_\alpha$
be the indicator variable that takes value 1 if
${\mathbf{1}}_\alpha$
be the indicator variable that takes value 1 if
![]() $\alpha \subseteq G^m_n$
, and 0 otherwise. The number
$\alpha \subseteq G^m_n$
, and 0 otherwise. The number
![]() $W_n$
of copies of
$W_n$
of copies of
![]() $H$
in
$H$
in
![]() $G^m_n$
is thus
$G^m_n$
is thus
and we are therefore interested in approximating the distribution of this sum.
Example 2.1.
For a simple example, let
![]() $H$
be a triangle. Then, a potential copy of
$H$
be a triangle. Then, a potential copy of
![]() $H$
in
$H$
in
![]() $G^m_n$
is described by its vertex set
$G^m_n$
is described by its vertex set
![]() ${\{i,j,k\}}\subseteq [n]$
, where we may assume
${\{i,j,k\}}\subseteq [n]$
, where we may assume
![]() $i\lt j\lt k$
, together with its edges
$i\lt j\lt k$
, together with its edges
![]() $ji^{(a)}$
,
$ji^{(a)}$
,
![]() $ki^{(b)}$
, and
$ki^{(b)}$
, and
![]() $kj^{(c)}$
, where
$kj^{(c)}$
, where
![]() $a,b,c\in [m]$
and
$a,b,c\in [m]$
and
![]() $b\neq c$
.
$b\neq c$
.
Remark 2.2. Let
![]() $m_H$
be the largest integer
$m_H$
be the largest integer
![]() $k$
such that the
$k$
such that the
![]() $k$
-core of
$k$
-core of
![]() $H$
is non-empty, i.e., there exists a non-empty subgraph of
$H$
is non-empty, i.e., there exists a non-empty subgraph of
![]() $H$
where each node has degree at least
$H$
where each node has degree at least
![]() $k$
(in the subgraph). For example,
$k$
(in the subgraph). For example,
![]() $m_H=1$
if
$m_H=1$
if
![]() $H$
is a tree,
$H$
is a tree,
![]() $m_H=2$
if
$m_H=2$
if
![]() $H$
is a cycle, and
$H$
is a cycle, and
![]() $m_H=k-1$
if
$m_H=k-1$
if
![]() $H$
is the complete graph on
$H$
is the complete graph on
![]() $k$
vertices. Then it is easy to see that if
$k$
vertices. Then it is easy to see that if
![]() $m\lt m_H$
, then there are no potential copies of
$m\lt m_H$
, then there are no potential copies of
![]() $H$
in
$H$
in
![]() $G^m_n$
for any
$G^m_n$
for any
![]() $n$
(since in a copy of
$n$
(since in a copy of
![]() $H$
, the vertex with largest label in the
$H$
, the vertex with largest label in the
![]() $m_H$
-core has at least
$m_H$
-core has at least
![]() $m_H$
edges to vertices with smaller labels); hence
$m_H$
edges to vertices with smaller labels); hence
![]() $\Gamma =\emptyset$
and thus
$\Gamma =\emptyset$
and thus
![]() $W_n=0$
deterministically. On the other hand, if
$W_n=0$
deterministically. On the other hand, if
![]() $m\geqslant m_H$
and
$m\geqslant m_H$
and
![]() $n$
is large enough, then there are potential copies (since we may create a copy by assigning labels in decreasing order to the vertices of
$n$
is large enough, then there are potential copies (since we may create a copy by assigning labels in decreasing order to the vertices of
![]() $H$
, each time choosing a vertex that has at most
$H$
, each time choosing a vertex that has at most
![]() $m_H$
edges to the remaining vertices).
$m_H$
edges to the remaining vertices).
Remark 2.3. Recall that
![]() $G^m_n$
is a loop-less multigraph. Similarly,
$G^m_n$
is a loop-less multigraph. Similarly,
![]() $H$
can be a loop-less multigraph in the results below, although we for simplicity write “graph” and “subgraph”.
$H$
can be a loop-less multigraph in the results below, although we for simplicity write “graph” and “subgraph”.
2.1. Probability distances
To precisely state our results, we also need to define the metrics in consideration here. The total variation distance
![]() $\mathop{d_{\mathrm{TV}}}$
between two probability measures
$\mathop{d_{\mathrm{TV}}}$
between two probability measures
![]() $\nu _1$
and
$\nu _1$
and
![]() $\nu _2$
supported on
$\nu _2$
supported on
![]() $\mathbb{Z}^+$
is defined as
$\mathbb{Z}^+$
is defined as
and the Wasserstein distance
![]() $\mathop{d_{\mathrm{W}}}$
between two probability measures
$\mathop{d_{\mathrm{W}}}$
between two probability measures
![]() $\nu _1,\nu _2$
supported on
$\nu _1,\nu _2$
supported on
![]() $\mathbb{R}$
is defined as
$\mathbb{R}$
is defined as
where the supremum is over all
![]() $f\,:\,\mathbb{R}\to \mathbb{R}$
such that
$f\,:\,\mathbb{R}\to \mathbb{R}$
such that
![]() $| f(x)-f(y)|\leqslant | x-y|$
for any
$| f(x)-f(y)|\leqslant | x-y|$
for any
![]() $x,y\in \mathbb{R}$
. Note that if, for example,
$x,y\in \mathbb{R}$
. Note that if, for example,
![]() $Y$
is a random variable with the standard normal distribution
$Y$
is a random variable with the standard normal distribution
![]() $\mathcal{N}(0,1)$
, then for any random variable
$\mathcal{N}(0,1)$
, then for any random variable
![]() $X$
, the usual Kolmogorov distance can be bounded by
$X$
, the usual Kolmogorov distance can be bounded by
(see e.g. [[Reference Ross17], Proposition 2.1]).
2.2. Further notation
We sometimes tacitly assume that
![]() $n$
is not too small.
$n$
is not too small.
![]() $\overset{\mathrm{a.s.}}{\longrightarrow }$
and
$\overset{\mathrm{a.s.}}{\longrightarrow }$
and
![]() $\overset{\mathrm{p}}{\longrightarrow }$
denote convergence almost surely (a.s.) and in probability, respectively.
$\overset{\mathrm{p}}{\longrightarrow }$
denote convergence almost surely (a.s.) and in probability, respectively.
![]() $\mathrm{Po}(\mu )$
denotes the Poisson distribution with mean
$\mathrm{Po}(\mu )$
denotes the Poisson distribution with mean
![]() $\mu$
, and
$\mu$
, and
![]() $\mathcal{N}(0,1)$
is the standard normal distribution.
$\mathcal{N}(0,1)$
is the standard normal distribution.
![]() $C$
denotes constants that may vary from one occurrence to the next. They do not depend on
$C$
denotes constants that may vary from one occurrence to the next. They do not depend on
![]() $n$
, but they may depend on
$n$
, but they may depend on
![]() $m$
,
$m$
,
![]() $H$
, and other parameters.
$H$
, and other parameters.
3. Main results
Consider first subgraphs that are cycles. The first two theorems show that when
![]() $n$
is large, the count of any cycle with a fixed number of edges is approximately Poisson, and that the joint distribution of the counts of cycles of different numbers of edges can be approximated by independent Poisson variables. For convenience, we refer to a cycle with
$n$
is large, the count of any cycle with a fixed number of edges is approximately Poisson, and that the joint distribution of the counts of cycles of different numbers of edges can be approximated by independent Poisson variables. For convenience, we refer to a cycle with
![]() $\ell$
edges and vertices simply as an
$\ell$
edges and vertices simply as an
![]() $\ell$
-cycle. Note also we view a pair of parallel edges as a 2-cycle.
$\ell$
-cycle. Note also we view a pair of parallel edges as a 2-cycle.
Theorem 3.1.
Fixing the positive integers
![]() $m\ge 2$
and
$m\ge 2$
and
![]() $\ell \geqslant 2$
, let
$\ell \geqslant 2$
, let
![]() $W_n$
be the number of
$W_n$
be the number of
![]() $\ell$
-cycles in
$\ell$
-cycles in
![]() $G^m_n$
, and let
$G^m_n$
, and let
![]() $\mu _n\,:\!=\,{\mathbb{E}} W_n$
. Then,
$\mu _n\,:\!=\,{\mathbb{E}} W_n$
. Then,
and there is a positive constant
![]() $C=C(m,\ell )$
such that
$C=C(m,\ell )$
such that
Remark 3.2. Let
![]() $W_n$
be as above and
$W_n$
be as above and
![]() $Y^{\prime}_n\sim \mathrm{Po}(\mu _n)$
and define
$Y^{\prime}_n\sim \mathrm{Po}(\mu _n)$
and define
It follows from Theorem 3.1 that
On the other hand, the classical Berry–Esseen theorem implies that
Combining (3.4) and (3.5) with the triangle inequality, and using (3.1), we obtain
In particular, the cycle count
![]() $W_n$
is asymptotically normal. In fact, the estimate (3.6) is sharp. Since
$W_n$
is asymptotically normal. In fact, the estimate (3.6) is sharp. Since
![]() $\mathcal N(0,1)$
has a continuous distribution function, while the distribution function of
$\mathcal N(0,1)$
has a continuous distribution function, while the distribution function of
![]() $Z_n$
has a jump
$Z_n$
has a jump
![]() $\mathbb{P}(W_n=k)$
(if this is non-zero) at
$\mathbb{P}(W_n=k)$
(if this is non-zero) at
![]() $(k-\mu _n)/\sqrt{\mu _n}$
, it follows by choosing
$(k-\mu _n)/\sqrt{\mu _n}$
, it follows by choosing
![]() $k=\lfloor{\mu _n}\rfloor$
and using (3.2) and (3.1) that
$k=\lfloor{\mu _n}\rfloor$
and using (3.2) and (3.1) that
Consequently, combining (3.5) and (3.7),
In the following corresponding theorem on multi-variate Poisson approximation, the error bound that we obtain is slightly inferior to the one in Theorem3.1. As in Remark 3.2, this theorem implies also a multivariate normal approximation (we omit the details).
Theorem 3.3.
Fix the positive integers
![]() $m,r\ge 2$
and
$m,r\ge 2$
and
![]() $\ell (i)\in [2,\infty )$
,
$\ell (i)\in [2,\infty )$
,
![]() $i\in [r]$
, with
$i\in [r]$
, with
![]() $\ell (i)\ne \ell (j)$
for
$\ell (i)\ne \ell (j)$
for
![]() $i\ne j$
. Let
$i\ne j$
. Let
![]() $W^{(i)}_n$
be the number of cycles of length
$W^{(i)}_n$
be the number of cycles of length
![]() $\ell (i)$
in
$\ell (i)$
in
![]() $G^m_n$
, and let
$G^m_n$
, and let
![]() $\mu _{n,i}\,:\!=\,{\mathbb{E}} W_n^{(i)}$
. Then, there is a positive constant
$\mu _{n,i}\,:\!=\,{\mathbb{E}} W_n^{(i)}$
. Then, there is a positive constant
![]() $C=C(m,(\ell (i))_{i\in [r]})$
such that
$C=C(m,(\ell (i))_{i\in [r]})$
such that
 \begin{equation} \mathop{d_{\mathrm{TV}}}\left (\mathcal{L}(\left \{{W^{(i)}_n}\right \}^r_{i=1}), \prod ^r_{i=1}\mathrm{Po}(\mu _{n,i})\right )\leqslant \frac{C\log \log n}{\log n}. \end{equation}
\begin{equation} \mathop{d_{\mathrm{TV}}}\left (\mathcal{L}(\left \{{W^{(i)}_n}\right \}^r_{i=1}), \prod ^r_{i=1}\mathrm{Po}(\mu _{n,i})\right )\leqslant \frac{C\log \log n}{\log n}. \end{equation}
Example 3.4.
The case
![]() $\ell =2$
is simple in Theorems 3.1 and 3.3, since the numbers of pairs of parallel edges with larger endpoint
$\ell =2$
is simple in Theorems 3.1 and 3.3, since the numbers of pairs of parallel edges with larger endpoint
![]() $j$
are independent for different
$j$
are independent for different
![]() $j$
; moreover, we have the exact formula
$j$
; moreover, we have the exact formula
![]() $\mu _n=\binom m2\sum _{j=2}^n\frac{1}{j-1}$
. For
$\mu _n=\binom m2\sum _{j=2}^n\frac{1}{j-1}$
. For
![]() $\ell =3$
, Example 2.1 yields
$\ell =3$
, Example 2.1 yields
Next, we state the normal approximation for the count of any unicyclic graph, i.e., a graph that contains exactly one cycle. For completeness, we include cycles in the theorem below. Let
![]() $\mathcal{C}_\ell$
be an
$\mathcal{C}_\ell$
be an
![]() $\ell$
-cycle, let
$\ell$
-cycle, let
![]() $s\ge 0$
, and let, for
$s\ge 0$
, and let, for
![]() $i=1,\dots, s$
,
$i=1,\dots, s$
,
![]() $\mathcal{T}_i$
be a tree with
$\mathcal{T}_i$
be a tree with
![]() $t_i$
edges and a distinguished root, so that
$t_i$
edges and a distinguished root, so that
![]() $\mathcal{T}_i$
has
$\mathcal{T}_i$
has
![]() $t_i+1$
vertices. We consider a graph
$t_i+1$
vertices. We consider a graph
![]() $\Lambda \,:\!=\,\Lambda _{\ell, t_1,\dots, t_s}$
which can be constructed by attaching each
$\Lambda \,:\!=\,\Lambda _{\ell, t_1,\dots, t_s}$
which can be constructed by attaching each
![]() $\mathcal{T}_i$
to
$\mathcal{T}_i$
to
![]() $\mathcal{C}_\ell$
, using a vertex of
$\mathcal{C}_\ell$
, using a vertex of
![]() $\mathcal{C}_\ell$
as the distinguished root of
$\mathcal{C}_\ell$
as the distinguished root of
![]() $\mathcal{T}_i$
. (This does not specify
$\mathcal{T}_i$
. (This does not specify
![]() $\Lambda$
uniquely, but we choose one possibility.) By combining the trees
$\Lambda$
uniquely, but we choose one possibility.) By combining the trees
![]() $\mathcal{T}_i$
that are attached at the same vertex in the cycle, we may assume that
$\mathcal{T}_i$
that are attached at the same vertex in the cycle, we may assume that
![]() $s\leqslant \ell$
and that each
$s\leqslant \ell$
and that each
![]() $\mathcal{T}_i$
is attached to
$\mathcal{T}_i$
is attached to
![]() $\mathcal{C}_\ell$
at a distinct vertex. Denote by
$\mathcal{C}_\ell$
at a distinct vertex. Denote by
![]() $\Gamma =\Gamma ^{(n,m)}_{\Lambda }$
the set of all potential copies of
$\Gamma =\Gamma ^{(n,m)}_{\Lambda }$
the set of all potential copies of
![]() $\Lambda$
; and saving notation, let
$\Lambda$
; and saving notation, let
Theorem 3.5.
Fixing the integers
![]() $m\ge 2$
,
$m\ge 2$
,
![]() $\ell \ge 2$
,
$\ell \ge 2$
,
![]() $s\ge 0$
,
$s\ge 0$
,
![]() $t_1,\dots, t_s\ge 1$
, and a unicyclic subgraph
$t_1,\dots, t_s\ge 1$
, and a unicyclic subgraph
![]() $\Lambda$
as above, let
$\Lambda$
as above, let
![]() $W_n$
,
$W_n$
,
![]() $\mu _n$
and
$\mu _n$
and
![]() $\sigma _n$
be as in (3.11), and
$\sigma _n$
be as in (3.11), and
![]() $Y_n\,:\!=\,(W_n-\mu _n)/\sigma _n$
. Let
$Y_n\,:\!=\,(W_n-\mu _n)/\sigma _n$
. Let
![]() $t=\sum ^s_{i=1}t_i\ge 0$
; then
$t=\sum ^s_{i=1}t_i\ge 0$
; then
and there is a positive constant
![]() $C=C(m,\ell, t)$
such that
$C=C(m,\ell, t)$
such that
Remark 3.6. In view of (2.4) and (3.14), Theorem 3.5 implies an error bound
for the Kolmogorov distance, which in the case of a cycle is clearly not as sharp as the error bound in (3.6).
The next theorem concerns trees, and the normal approximation result relies on the assumption that the variance of the counts of the tree of choice is of the exact order
![]() $\Theta (n)$
. The precise order of the variance in this case is much harder to establish, essentially due to the fact that the total covariance of the positively correlated pairs of copies and that of the negatively correlated pairs of copies are both of order
$\Theta (n)$
. The precise order of the variance in this case is much harder to establish, essentially due to the fact that the total covariance of the positively correlated pairs of copies and that of the negatively correlated pairs of copies are both of order
![]() $O(n)$
. However, we are able to prove that the variance of the count of a star is precisely
$O(n)$
. However, we are able to prove that the variance of the count of a star is precisely
![]() $\Theta (n)$
. Below, let
$\Theta (n)$
. Below, let
![]() $\Lambda$
be a fixed tree on
$\Lambda$
be a fixed tree on
![]() $t$
vertices, let
$t$
vertices, let
![]() $\Gamma$
be the set of potential copies of
$\Gamma$
be the set of potential copies of
![]() $\Lambda$
, and define again
$\Lambda$
, and define again
![]() $W_n,\mu _n$
, and
$W_n,\mu _n$
, and
![]() $\sigma ^2_n$
by (3.11).
$\sigma ^2_n$
by (3.11).
Theorem 3.7.
Fix the positive integers
![]() $m,t$
and the tree
$m,t$
and the tree
![]() $\Lambda$
with
$\Lambda$
with
![]() $t$
vertices. Let
$t$
vertices. Let
![]() $W_n,\mu _n$
and
$W_n,\mu _n$
and
![]() $\sigma _n$
be as above, and
$\sigma _n$
be as above, and
![]() $Y_n\,:\!=\,(W_n-\mu _n)/\sigma _n$
. Then
$Y_n\,:\!=\,(W_n-\mu _n)/\sigma _n$
. Then
If
![]() $\sigma _n^2=\Theta (n)$
, then there is a constant
$\sigma _n^2=\Theta (n)$
, then there is a constant
![]() $C=C(m,t)$
such that
$C=C(m,t)$
such that
In the trivial cases
![]() $t=1$
and
$t=1$
and
![]() $t=2$
(a single vertex and a single edge, respectively),
$t=2$
(a single vertex and a single edge, respectively),
![]() $W_n$
is deterministic and
$W_n$
is deterministic and
![]() $\sigma ^2_n=0$
; thus
$\sigma ^2_n=0$
; thus
![]() $Y_n$
is not even defined. We conjecture that these are the only cases where (3.18) does not hold.
$Y_n$
is not even defined. We conjecture that these are the only cases where (3.18) does not hold.
Conjecture 3.8.
If
![]() $\Lambda$
is tree with at least 2 edges, then
$\Lambda$
is tree with at least 2 edges, then
![]() $\sigma ^2_n=\Theta (n)$
, and thus the normal approximation (3.18) holds.
$\sigma ^2_n=\Theta (n)$
, and thus the normal approximation (3.18) holds.
We show in Section 9.2 that this holds at least for stars.
Theorem 3.9.
Conjecture 3.8 holds when
![]() $\Lambda$
is a star
$\Lambda$
is a star
![]() $S_\ell$
with
$S_\ell$
with
![]() $\ell \ge 2$
edges.
$\ell \ge 2$
edges.
The remaining subgraphs are the multicyclic ones. We consider in particular the ones that have the following properties.
Definition 3.10. We say that a graph is
-
• multicyclic if it has at least two (not necessarily edge- or vertex-disjoint) cycles;
-
• leaf-free if it has no node of degree 1.
As examples of connected graphs that are both multicyclic and leaf-free, we have two edge-disjoint cycles joined by an edge, or two cycles that share precisely an edge; see Figure 2 for another example.
Theorem 3.11.
For any connected graph
![]() $H$
that is both multicyclic and leaf-free, and any
$H$
that is both multicyclic and leaf-free, and any
![]() $m\geqslant 2$
, the expected number of copies of
$m\geqslant 2$
, the expected number of copies of
![]() $H$
in
$H$
in
![]() $G^m_n$
is bounded as
$G^m_n$
is bounded as
![]() $n\to \infty$
.
$n\to \infty$
.
Remark 3.12. We may define the infinite random graph
![]() $G^m_\infty$
with vertex set {1,2,…} as the union of
$G^m_\infty$
with vertex set {1,2,…} as the union of
![]() $G^m_n$
over all
$G^m_n$
over all
![]() $n\ge 1$
. Let
$n\ge 1$
. Let
![]() $H$
be any fixed graph and let as above
$H$
be any fixed graph and let as above
![]() $W_n$
be the number of copies of
$W_n$
be the number of copies of
![]() $H$
in
$H$
in
![]() $G^m_n$
; also, let
$G^m_n$
; also, let
![]() $W_\infty \le \infty$
be the number of copies of
$W_\infty \le \infty$
be the number of copies of
![]() $H$
in
$H$
in
![]() $G^m_\infty$
. Then, as
$G^m_\infty$
. Then, as
![]() ${n\to \infty }$
,
${n\to \infty }$
,
![]() $W_n\nearrow W_\infty$
. In particular,
$W_n\nearrow W_\infty$
. In particular,
![]() $W_n\overset{\mathrm{p}}{\longrightarrow } W_\infty$
, and since both (3.12)–(3.13) and (3.16)–(3.17) imply
$W_n\overset{\mathrm{p}}{\longrightarrow } W_\infty$
, and since both (3.12)–(3.13) and (3.16)–(3.17) imply
![]() $W_n\overset{\mathrm{p}}{\longrightarrow }+\infty$
, we see that if
$W_n\overset{\mathrm{p}}{\longrightarrow }+\infty$
, we see that if
![]() $H$
is unicyclic or a tree, then
$H$
is unicyclic or a tree, then
![]() $W_\infty =\infty$
a.s. On the other hand, Theorem 3.11 implies by monotone convergence that if
$W_\infty =\infty$
a.s. On the other hand, Theorem 3.11 implies by monotone convergence that if
![]() $H$
is multicyclic and leaf-free, then
$H$
is multicyclic and leaf-free, then
![]() ${\mathbb{E}} W_\infty \lt \infty$
and thus
${\mathbb{E}} W_\infty \lt \infty$
and thus
![]() $W_\infty \lt \infty$
a.s.
$W_\infty \lt \infty$
a.s.
Note further that since
![]() $W_n\overset{\mathrm{a.s.}}{\longrightarrow } W_\infty$
as
$W_n\overset{\mathrm{a.s.}}{\longrightarrow } W_\infty$
as
![]() ${n\to \infty }$
, in particular,
${n\to \infty }$
, in particular,
![]() $W_n$
converges in distribution to
$W_n$
converges in distribution to
![]() $W_\infty$
(without any normalisation). However, we do not expect that this limiting distribution has any nice form such as Poisson, since
$W_\infty$
(without any normalisation). However, we do not expect that this limiting distribution has any nice form such as Poisson, since
![]() $W_\infty$
is mainly determined by the random wirings of the first few edges in
$W_\infty$
is mainly determined by the random wirings of the first few edges in
![]() $G^m_n$
.
$G^m_n$
.
We also consider the expected counts of a graph that are multicyclic but not leaf-free. Note that every such graph
![]() $H$
can be constructed in the following way. Start with a graph
$H$
can be constructed in the following way. Start with a graph
![]() $H^{\prime}$
that is both multicyclic and leaf-free, and let
$H^{\prime}$
that is both multicyclic and leaf-free, and let
![]() $\mathcal{T}_i$
,
$\mathcal{T}_i$
,
![]() $i=1,\ldots, s$
be trees with
$i=1,\ldots, s$
be trees with
![]() $t_i$
edges and a distinguished root. The graph
$t_i$
edges and a distinguished root. The graph
![]() $H$
is obtained by attaching every
$H$
is obtained by attaching every
![]() $\mathcal{T}_i$
to
$\mathcal{T}_i$
to
![]() $H^{\prime}$
, with one of the vertices of
$H^{\prime}$
, with one of the vertices of
![]() $H^{\prime}$
as the distinguished root of
$H^{\prime}$
as the distinguished root of
![]() $\mathcal{T}_i$
. As before, we may assume that any pair of
$\mathcal{T}_i$
. As before, we may assume that any pair of
![]() $\mathcal{T}_i$
do not share the same vertex of
$\mathcal{T}_i$
do not share the same vertex of
![]() $H^{\prime}$
. The graph
$H^{\prime}$
. The graph
![]() $H^{\prime}$
is known as the
$H^{\prime}$
is known as the
![]() $2$
-core of
$2$
-core of
![]() $H$
. See Figure 2 for an example.
$H$
. See Figure 2 for an example.

Figure 2. Left: a graph that is both multicyclic and leaf-free. Right: a graph that is multicyclic but not leaf-free.
In the following theorem, we for convenience include the case
![]() $t=0$
, which is just Theorem3.11. (Then
$t=0$
, which is just Theorem3.11. (Then
![]() $s=0$
and
$s=0$
and
![]() $H^{\prime}=H$
.) Recall the definition of
$H^{\prime}=H$
.) Recall the definition of
![]() $m_H$
in Remark 2.2, and that
$m_H$
in Remark 2.2, and that
![]() $W_n=0$
if
$W_n=0$
if
![]() $m\lt m_H$
.
$m\lt m_H$
.
Theorem 3.13.
Fixing a connected multicyclic graph
![]() $H$
and a positive integer
$H$
and a positive integer
![]() $m\geqslant m_H$
, let
$m\geqslant m_H$
, let
![]() $W_n$
be the number of copies of
$W_n$
be the number of copies of
![]() $H$
in
$H$
in
![]() $G^m_n$
, and let
$G^m_n$
, and let
![]() $t\,:\!=\,\sum _i t_i\ge 0$
be the number of vertices in
$t\,:\!=\,\sum _i t_i\ge 0$
be the number of vertices in
![]() $H\setminus H^{\prime}$
, where
$H\setminus H^{\prime}$
, where
![]() $H^{\prime}$
as above is the
$H^{\prime}$
as above is the
![]() $2$
-core of
$2$
-core of
![]() $H$
. Then,
$H$
. Then,
The precise order of
![]() ${\mathrm{Var}}(W_n)$
is more difficult to establish for the same reason as for trees. For this family of graphs, we do not expect the count to be approximately Poisson or normal (after renormalisation). Instead, we make the following conjecture, where we, as commented above, do not expect the distribution of the limit to have a nice form.
${\mathrm{Var}}(W_n)$
is more difficult to establish for the same reason as for trees. For this family of graphs, we do not expect the count to be approximately Poisson or normal (after renormalisation). Instead, we make the following conjecture, where we, as commented above, do not expect the distribution of the limit to have a nice form.
Conjecture 3.14.
Let
![]() $H$
and
$H$
and
![]() $H^{\prime}$
be as in Theorem 3.13, and let
$H^{\prime}$
be as in Theorem 3.13, and let
![]() $W_n$
and
$W_n$
and
![]() $W^{\prime}_n$
be the numbers of copies of
$W^{\prime}_n$
be the numbers of copies of
![]() $H$
and
$H$
and
![]() $H^{\prime}$
in
$H^{\prime}$
in
![]() $G^m_n$
, respectively. Then there exists a constant
$G^m_n$
, respectively. Then there exists a constant
![]() $c\gt 0$
such that
$c\gt 0$
such that
![]() $(\log n)^{-t}W_n-c W^{\prime}_n \overset{\mathrm{a.s.}}{\longrightarrow } 0$
as
$(\log n)^{-t}W_n-c W^{\prime}_n \overset{\mathrm{a.s.}}{\longrightarrow } 0$
as
![]() ${n\to \infty }$
, and thus
${n\to \infty }$
, and thus
We can prove a special case. It appears likely that the general case can be shown by similar arguments, but the details seem complicated and we leave this as an open problem.
Theorem 3.15.
Conjecture 3.14 holds when
![]() $t=1$
.
$t=1$
.
We note also that at least for some multicyclic graphs
![]() $H^{\prime}$
,
$H^{\prime}$
,
![]() $W^{\prime}_\infty =0$
with positive probability, and thus
$W^{\prime}_\infty =0$
with positive probability, and thus
![]() $\mathbb{P}(W_\infty =0)\geqslant \mathbb{P}(W^{\prime}_\infty =0)\gt 0$
; hence although
$\mathbb{P}(W_\infty =0)\geqslant \mathbb{P}(W^{\prime}_\infty =0)\gt 0$
; hence although
![]() ${\mathbb{E}} W_n\to \infty$
by (3.19),
${\mathbb{E}} W_n\to \infty$
by (3.19),
![]() $\mathbb{P}(W_n=0)\geqslant c\gt 0$
, which in particular shows that we cannot have Poisson or normal convergence. We do not know whether this holds for every simple multigraph
$\mathbb{P}(W_n=0)\geqslant c\gt 0$
, which in particular shows that we cannot have Poisson or normal convergence. We do not know whether this holds for every simple multigraph
![]() $H^{\prime}$
, and we give just one example.
$H^{\prime}$
, and we give just one example.
Example 3.16.
Let
![]() $H^{\prime}$
be the complete graph on 4 vertices,
$H^{\prime}$
be the complete graph on 4 vertices,
![]() $K_4$
, and construct
$K_4$
, and construct
![]() $H$
by adding a single edge to
$H$
by adding a single edge to
![]() $H^{\prime}$
; thus we take
$H^{\prime}$
; thus we take
![]() $s=1$
and
$s=1$
and
![]() $\mathcal{T}_1$
as an edge in the construction above. Let
$\mathcal{T}_1$
as an edge in the construction above. Let
![]() $W_n$
and
$W_n$
and
![]() $W^{\prime}_n$
be as above. By Theorem 3.11 (or a simple calculation), we see that a.s.
$W^{\prime}_n$
be as above. By Theorem 3.11 (or a simple calculation), we see that a.s.
![]() $W^{\prime}_n\to W^{\prime}_\infty \lt \infty$
as
$W^{\prime}_n\to W^{\prime}_\infty \lt \infty$
as
![]() $n\to \infty$
. Moreover, we claim that
$n\to \infty$
. Moreover, we claim that
![]() $\mathbb{P}(W^{\prime}_\infty =0)\gt 0$
.
$\mathbb{P}(W^{\prime}_\infty =0)\gt 0$
.
To see this, let
![]() $H^{\prime\prime}=K_4^-$
be
$H^{\prime\prime}=K_4^-$
be
![]() $K_4$
minus one edge, and let
$K_4$
minus one edge, and let
![]() $W_n^{\prime\prime}$
be the number of copies of
$W_n^{\prime\prime}$
be the number of copies of
![]() $K_4^-$
in
$K_4^-$
in
![]() $G^m_n$
. Fix a large
$G^m_n$
. Fix a large
![]() $N$
, and consider only
$N$
, and consider only
![]() $n\gt N$
. Let
$n\gt N$
. Let
![]() ${\mathcal{E}}_N^{\prime}$
be the event that there is a triangle in
${\mathcal{E}}_N^{\prime}$
be the event that there is a triangle in
![]() $G^m_N$
. Let
$G^m_N$
. Let
![]() ${\mathcal{E}}_{N,n}^{\prime\prime}$
be the event that there is a copy of
${\mathcal{E}}_{N,n}^{\prime\prime}$
be the event that there is a copy of
![]() $K_4$
in
$K_4$
in
![]() $G^m_n\cup K^m_N$
with at most 2 vertices in
$G^m_n\cup K^m_N$
with at most 2 vertices in
![]() $[N]$
. In other words
$[N]$
. In other words
![]() ${\mathcal{E}}^{\prime\prime}_{N,n}$
means that there is either a copy of
${\mathcal{E}}^{\prime\prime}_{N,n}$
means that there is either a copy of
![]() $K_4$
in
$K_4$
in
![]() $G^m_n$
, or a copy of
$G^m_n$
, or a copy of
![]() $K_4^-$
in
$K_4^-$
in
![]() $G^m_n$
with the two non-adjacent vertices in
$G^m_n$
with the two non-adjacent vertices in
![]() $[N]$
and the two others in
$[N]$
and the two others in
![]() $[n]\setminus [N]$
. Note that
$[n]\setminus [N]$
. Note that
![]() ${\mathcal{E}}_{N,n}^{\prime\prime}$
does not depend on the edges of
${\mathcal{E}}_{N,n}^{\prime\prime}$
does not depend on the edges of
![]() $G^m_N$
, and thus
$G^m_N$
, and thus
![]() ${\mathcal{E}}_N^{\prime}$
and
${\mathcal{E}}_N^{\prime}$
and
![]() ${\mathcal{E}}_{N,n}^{\prime\prime}$
are independent. If there is a copy of
${\mathcal{E}}_{N,n}^{\prime\prime}$
are independent. If there is a copy of
![]() $K_4$
in
$K_4$
in
![]() $G^m_n$
, then either
$G^m_n$
, then either
![]() ${\mathcal{E}}_N^{\prime}$
or
${\mathcal{E}}_N^{\prime}$
or
![]() ${\mathcal{E}}_{N,n}^{\prime\prime}$
holds, and thus
${\mathcal{E}}_{N,n}^{\prime\prime}$
holds, and thus
If
![]() ${\mathcal{E}}_{N,n}^{\prime\prime}$
holds, then there is a copy of
${\mathcal{E}}_{N,n}^{\prime\prime}$
holds, then there is a copy of
![]() $H^{\prime\prime}=K_4^-$
in
$H^{\prime\prime}=K_4^-$
in
![]() $G^m_n$
with at least two vertices in
$G^m_n$
with at least two vertices in
![]() $[n]\setminus [N]$
, and thus
$[n]\setminus [N]$
, and thus
![]() $W^{\prime\prime}_\infty \geqslant W^{\prime\prime}_n \geqslant W^{\prime\prime}_N+1$
. Hence, by Markov’s inequality,
$W^{\prime\prime}_\infty \geqslant W^{\prime\prime}_n \geqslant W^{\prime\prime}_N+1$
. Hence, by Markov’s inequality,
Since
![]() ${\mathbb{E}} W_N^{\prime\prime}\to{\mathbb{E}} W_\infty ^{\prime\prime}$
as
${\mathbb{E}} W_N^{\prime\prime}\to{\mathbb{E}} W_\infty ^{\prime\prime}$
as
![]() ${N\to \infty }$
, we can choose
${N\to \infty }$
, we can choose
![]() $N$
such that
$N$
such that
![]() ${\mathbb{E}} W_\infty ^{\prime\prime}-{\mathbb{E}} W_N^{\prime\prime}\le \frac 12$
; then (3.23) implies that
${\mathbb{E}} W_\infty ^{\prime\prime}-{\mathbb{E}} W_N^{\prime\prime}\le \frac 12$
; then (3.23) implies that
![]() $\mathbb{P}(\text{not }{\mathcal{E}}_{N,n}^{\prime\prime})\geqslant \frac 12$
for all
$\mathbb{P}(\text{not }{\mathcal{E}}_{N,n}^{\prime\prime})\geqslant \frac 12$
for all
![]() $n\gt N$
. Moreover,
$n\gt N$
. Moreover,
![]() $\mathbb{P}(\text{not }{\mathcal{E}}_N^{\prime})\gt 0$
, since there is a positive probability that all edges in
$\mathbb{P}(\text{not }{\mathcal{E}}_N^{\prime})\gt 0$
, since there is a positive probability that all edges in
![]() $G^m_N$
lead to 1, and then there is no triangle. Consequently, (3.22) yields
$G^m_N$
lead to 1, and then there is no triangle. Consequently, (3.22) yields
![]() $\mathbb{P}(W_n^{\prime}=0)\geqslant c$
, for some
$\mathbb{P}(W_n^{\prime}=0)\geqslant c$
, for some
![]() $c\gt 0$
that does not depend on
$c\gt 0$
that does not depend on
![]() $n\gt N$
; thus also
$n\gt N$
; thus also
![]() $\mathbb{P}(W^{\prime}_\infty =0)\geqslant c\gt 0$
.
$\mathbb{P}(W^{\prime}_\infty =0)\geqslant c\gt 0$
.
If there are no copies of
![]() $H^{\prime}$
, then there can be no copies of
$H^{\prime}$
, then there can be no copies of
![]() $H$
, and thus we conclude
$H$
, and thus we conclude
![]() $\mathbb{P}(W_n=0)\geqslant c\gt 0$
for all
$\mathbb{P}(W_n=0)\geqslant c\gt 0$
for all
![]() $n$
. Hence, although
$n$
. Hence, although
![]() ${\mathbb{E}} W_n\to \infty$
by (3.19),
${\mathbb{E}} W_n\to \infty$
by (3.19),
![]() $W_n$
does not converge in probability to
$W_n$
does not converge in probability to
![]() $+\infty$
, and in particular
$+\infty$
, and in particular
![]() $W_n$
cannot be asymptotically normal.
$W_n$
cannot be asymptotically normal.
3.1. Discussion on possible future avenues
An important direction for future work is to verify if Conjecture 3.8 holds, or in other words, to prove that the variance of the count of any tree with at least 2 edges is of the precise order
![]() $n$
. Another direction for future work is to compute the leading coefficients of the means and variances of the subgraph counts. More precise expressions will possibly also enable us to verify if the approximation results still hold if
$n$
. Another direction for future work is to compute the leading coefficients of the means and variances of the subgraph counts. More precise expressions will possibly also enable us to verify if the approximation results still hold if
![]() $m$
and (or) the number of vertices of the subgraph are allowed to increase with
$m$
and (or) the number of vertices of the subgraph are allowed to increase with
![]() $n$
. It is also possible to prove a multivariate analogue for the normal approximation results. This can be done using, for instance, [[Reference Chen, Goldstein and Shao4], Theorem 12.1], which also uses Stein’s method with the size-bias coupling.
$n$
. It is also possible to prove a multivariate analogue for the normal approximation results. This can be done using, for instance, [[Reference Chen, Goldstein and Shao4], Theorem 12.1], which also uses Stein’s method with the size-bias coupling.
3.2. Article outline
In the next section, we state the results from Stein’s method that we apply in the approximation proofs. These results use a coupling that we construct in Section 5. In Section 6, we prove Theorem3.11 and some additional lemmas that will be useful in the approximation proofs later. We prove the Poisson approximation results (Theorems3.1 and 3.3) in Section 7 and the normal approximation for unicyclic graphs (Theorem 3.5) in Section 8, where we also prove Theorem3.13. Section 9 contains the proofs of the normal approximation for trees (Theorems3.7 and 3.9), and in the last section we give a proof of Theorem 3.15.
4. Preliminary: Stein’s method
The error bounds in the Poisson and normal approximation results that we use are obtained from general results on Stein’s method in terms of a coupling that we now describe. Let
![]() $(I_\alpha )_{\alpha \in \Gamma }$
be a collection of 0-1 valued random variables. For each
$(I_\alpha )_{\alpha \in \Gamma }$
be a collection of 0-1 valued random variables. For each
![]() $\alpha \in \Gamma$
, let the random variables
$\alpha \in \Gamma$
, let the random variables
![]() $(J_{\beta \alpha })_{\beta \in \Gamma }$
be defined on the same space as
$(J_{\beta \alpha })_{\beta \in \Gamma }$
be defined on the same space as
![]() $(I_\alpha )_{\alpha \in \Gamma }$
, satisfying
$(I_\alpha )_{\alpha \in \Gamma }$
, satisfying
Note that this is a special case of the size-bias coupling appearing in the literature of Stein’s method; see [Reference Chen, Goldstein and Shao4, Reference Ross17], and also [Reference Goldstein and Rinott12]. The theorem below is a direct consequence of [[Reference Barbour, Holst and Janson2], Chapter 2, equation (1.2)].
Theorem 4.1.
Let
![]() $(I_\alpha )_{\alpha \in \Gamma }$
be as above, where
$(I_\alpha )_{\alpha \in \Gamma }$
be as above, where
![]() ${\mathbb{E}} I_\alpha =\pi _\alpha$
. Suppose that for each
${\mathbb{E}} I_\alpha =\pi _\alpha$
. Suppose that for each
![]() $\alpha \in \Gamma$
, there is a coupling of
$\alpha \in \Gamma$
, there is a coupling of
![]() $(J_{\beta \alpha })_{\beta \in \Gamma }$
and
$(J_{\beta \alpha })_{\beta \in \Gamma }$
and
![]() $(I_\alpha )_{\alpha \in \Gamma }$
such that (4.1) holds. Let
$(I_\alpha )_{\alpha \in \Gamma }$
such that (4.1) holds. Let
![]() $W\,:\!=\,\sum _{\alpha \in \Gamma }I_\alpha$
,
$W\,:\!=\,\sum _{\alpha \in \Gamma }I_\alpha$
,
![]() $\lambda \,:\!=\,\sum _{\alpha \in \Gamma }\pi _\alpha$
. Then,
$\lambda \,:\!=\,\sum _{\alpha \in \Gamma }\pi _\alpha$
. Then,
 \begin{equation} \mathop{d_{\mathrm{TV}}}(\mathcal{L}(W),\mathrm{Po}(\lambda ))\leqslant \min \left \{{1,\lambda ^{-1}}\right \}\left (\sum _{\alpha \in \Gamma }\pi ^2_\alpha +\sum _{\alpha \in \Gamma } \sum _{\beta \not =\alpha }\pi _\alpha{\mathbb{E}} | J_{\beta \alpha }-I_\beta |\right ). \end{equation}
\begin{equation} \mathop{d_{\mathrm{TV}}}(\mathcal{L}(W),\mathrm{Po}(\lambda ))\leqslant \min \left \{{1,\lambda ^{-1}}\right \}\left (\sum _{\alpha \in \Gamma }\pi ^2_\alpha +\sum _{\alpha \in \Gamma } \sum _{\beta \not =\alpha }\pi _\alpha{\mathbb{E}} | J_{\beta \alpha }-I_\beta |\right ). \end{equation}
Now, assume that there is a partition
![]() $\Gamma =\bigcup ^r_{j=1}\Gamma _j$
. The next theorem quantifies how well the random vector
$\Gamma =\bigcup ^r_{j=1}\Gamma _j$
. The next theorem quantifies how well the random vector
![]() $(\sum _{\alpha \in \Gamma _j}I_\alpha )_{1\leqslant j\leqslant r}$
can be approximated by a vector of independent Poisson variables. In our application,
$(\sum _{\alpha \in \Gamma _j}I_\alpha )_{1\leqslant j\leqslant r}$
can be approximated by a vector of independent Poisson variables. In our application,
![]() $\Gamma _j$
is to be taken as the set of potential cycles of length
$\Gamma _j$
is to be taken as the set of potential cycles of length
![]() $\ell (j)$
.
$\ell (j)$
.
Theorem 4.2 ([ [Reference Barbour, Holst and Janson2], Theorem 10.K]). Let
![]() $W_j=\sum _{\alpha \in \Gamma _j}I_\alpha$
,
$W_j=\sum _{\alpha \in \Gamma _j}I_\alpha$
,
![]() ${\mathbb{E}} I_\alpha =\pi _\alpha$
and
${\mathbb{E}} I_\alpha =\pi _\alpha$
and
![]() $\lambda _j={\mathbb{E}} W_j$
. Suppose that for each
$\lambda _j={\mathbb{E}} W_j$
. Suppose that for each
![]() $\alpha \in \Gamma$
, there is a coupling of
$\alpha \in \Gamma$
, there is a coupling of
![]() $(J_{\beta \alpha })_{\beta \in \Gamma }$
and
$(J_{\beta \alpha })_{\beta \in \Gamma }$
and
![]() $(I_\alpha )_{\alpha \in \Gamma }$
such that (4.1) holds. Then,
$(I_\alpha )_{\alpha \in \Gamma }$
such that (4.1) holds. Then,
 \begin{equation} \mathop{d_{\mathrm{TV}}}\left ({\mathcal{L}(\left \{{W_j}\right \}^r_{j=1}), \prod ^r_{j=1}\mathrm{Po}(\lambda _j)}\right )\leqslant \frac{1+2\log ^+(e\min _j \lambda _j)}{e\min _j\lambda _j}\sum _{\alpha \in \Gamma } \left ({\pi ^2_\alpha + \sum _{\beta \not =\alpha }\pi _\alpha{\mathbb{E}} | J_{\beta \alpha }-I_\beta |}\right ). \end{equation}
\begin{equation} \mathop{d_{\mathrm{TV}}}\left ({\mathcal{L}(\left \{{W_j}\right \}^r_{j=1}), \prod ^r_{j=1}\mathrm{Po}(\lambda _j)}\right )\leqslant \frac{1+2\log ^+(e\min _j \lambda _j)}{e\min _j\lambda _j}\sum _{\alpha \in \Gamma } \left ({\pi ^2_\alpha + \sum _{\beta \not =\alpha }\pi _\alpha{\mathbb{E}} | J_{\beta \alpha }-I_\beta |}\right ). \end{equation}
We now state a normal approximation result for a collection of 0-1 variables, which follows from [[Reference Ross17], Theorem 3.20 and Corollary 3.24].
Theorem 4.3.
Let
![]() $(I_\alpha )_{\alpha \in \Gamma }$
be a collection of
$(I_\alpha )_{\alpha \in \Gamma }$
be a collection of
![]() $0$
-
$0$
-
![]() $1$
variables and let
$1$
variables and let
![]() $(J_{\beta \alpha })_{\beta \in \Gamma }$
be defined on the same space as
$(J_{\beta \alpha })_{\beta \in \Gamma }$
be defined on the same space as
![]() $(I_\alpha )_{\alpha \in \Gamma }$
, satisfying (4.1). Define
$(I_\alpha )_{\alpha \in \Gamma }$
, satisfying (4.1). Define
![]() $W\,:\!=\,\sum _{\alpha \in \Gamma }I_\alpha$
,
$W\,:\!=\,\sum _{\alpha \in \Gamma }I_\alpha$
,
![]() $\mu \,:\!=\,{\mathbb{E}} W$
,
$\mu \,:\!=\,{\mathbb{E}} W$
,
![]() $\sigma ^2\,:\!=\,{\mathrm{Var}}(W)$
and
$\sigma ^2\,:\!=\,{\mathrm{Var}}(W)$
and
![]() $W^s\,:\!=\, \sum _{\beta \in \Gamma \setminus \{K\}}J_{\beta K}+1$
, where the index
$W^s\,:\!=\, \sum _{\beta \in \Gamma \setminus \{K\}}J_{\beta K}+1$
, where the index
![]() $K\in \Gamma$
is chosen randomly with probabilities
$K\in \Gamma$
is chosen randomly with probabilities
![]() $\mathbb{P}(K=\alpha )={\mathbb{E}} I_\alpha /\mu$
. If
$\mathbb{P}(K=\alpha )={\mathbb{E}} I_\alpha /\mu$
. If
![]() $Z=(W-\mu )/\sigma$
, then
$Z=(W-\mu )/\sigma$
, then
where
![]() $\mathcal{N}(0,1)$
is the standard normal distribution.
$\mathcal{N}(0,1)$
is the standard normal distribution.
5. Construction of the size-bias couplings
As the edges of a uniform attachment graph are independent, we can construct the coupling appearing in Theorems4.1–4.3 as follows. Fix the subgraph
![]() $H$
, let
$H$
, let
![]() $G\,:\!=\,G^m_n$
be the uniform attachment graph and let
$G\,:\!=\,G^m_n$
be the uniform attachment graph and let
![]() $\Gamma$
be the set of potential copies of
$\Gamma$
be the set of potential copies of
![]() $H$
. For every
$H$
. For every
![]() $\alpha \in \Gamma$
, we couple two graphs
$\alpha \in \Gamma$
, we couple two graphs
![]() $G$
and
$G$
and
![]() $G^\alpha$
by matching their attachment steps, except for the edges of
$G^\alpha$
by matching their attachment steps, except for the edges of
![]() $\alpha$
. In
$\alpha$
. In
![]() $G^\alpha$
, the edges of
$G^\alpha$
, the edges of
![]() $\alpha$
are wired in a deterministic fashion to obtain the copy
$\alpha$
are wired in a deterministic fashion to obtain the copy
![]() $\alpha$
of
$\alpha$
of
![]() $H$
; whereas in
$H$
; whereas in
![]() $G$
, they are generated independently from the construction of
$G$
, they are generated independently from the construction of
![]() $G^\alpha$
. For
$G^\alpha$
. For
![]() $\beta \in \Gamma$
, let as above
$\beta \in \Gamma$
, let as above
![]() ${\mathbf{1}}_\beta$
be the indicator that the subgraph
${\mathbf{1}}_\beta$
be the indicator that the subgraph
![]() $\beta$
is present in
$\beta$
is present in
![]() $G$
, and let
$G$
, and let
![]() ${\mathbf{1}}^\alpha _\beta$
be the indicator that
${\mathbf{1}}^\alpha _\beta$
be the indicator that
![]() $\beta$
is present in
$\beta$
is present in
![]() $G^\alpha$
. It follows that for every chosen
$G^\alpha$
. It follows that for every chosen
![]() $\alpha$
,
$\alpha$
,
Let
![]() $\Gamma ^-_\alpha \subset \Gamma$
be the set of copies
$\Gamma ^-_\alpha \subset \Gamma$
be the set of copies
![]() $\beta$
of
$\beta$
of
![]() $H$
such that at least one edge of
$H$
such that at least one edge of
![]() $\alpha$
has a different endpoint in
$\alpha$
has a different endpoint in
![]() $\beta$
, and let
$\beta$
, and let
![]() $\Gamma ^+_\alpha \subset \Gamma \setminus \Gamma ^-_\alpha$
be the set of copies of
$\Gamma ^+_\alpha \subset \Gamma \setminus \Gamma ^-_\alpha$
be the set of copies of
![]() $H$
that share at least one edge with
$H$
that share at least one edge with
![]() $\alpha$
, excluding
$\alpha$
, excluding
![]() $\alpha$
itself. Observe that under the coupling,
$\alpha$
itself. Observe that under the coupling,
![]() ${\mathbf{1}}^\alpha _{\beta }\leqslant{\mathbf{1}}_\beta$
for
${\mathbf{1}}^\alpha _{\beta }\leqslant{\mathbf{1}}_\beta$
for
![]() $\beta \in \Gamma ^-_\alpha$
and
$\beta \in \Gamma ^-_\alpha$
and
![]() ${\mathbf{1}}^\alpha _{\beta }\geqslant{\mathbf{1}}_\beta$
for
${\mathbf{1}}^\alpha _{\beta }\geqslant{\mathbf{1}}_\beta$
for
![]() $\beta \in \Gamma ^+_\alpha$
, while
$\beta \in \Gamma ^+_\alpha$
, while
![]() ${\mathbf{1}}^\alpha _{\beta }={\mathbf{1}}_\beta$
for every
${\mathbf{1}}^\alpha _{\beta }={\mathbf{1}}_\beta$
for every
![]() $\beta \in \Gamma \setminus (\Gamma ^+_\alpha \cup \Gamma ^-_\alpha \cup \left \{{\alpha }\right \})$
. The error bound (4.2) in Theorem4.1 therefore simplifies to
$\beta \in \Gamma \setminus (\Gamma ^+_\alpha \cup \Gamma ^-_\alpha \cup \left \{{\alpha }\right \})$
. The error bound (4.2) in Theorem4.1 therefore simplifies to
 \begin{align} \text{min}\! \left \{{1,\lambda ^{-1}}\right \}\left (\sum _{\alpha \in \Gamma }\pi _\alpha ^2 + \sum _{\alpha \in \Gamma }\sum _{\beta \in \Gamma ^+_\alpha } \pi _\alpha{\mathbb{E}}[{\mathbf{1}}^\alpha _{\beta }-{\mathbf{1}}_\beta ] + \sum _{\alpha \in \Gamma }\sum _{\beta \in \Gamma ^-_\alpha } \pi _\alpha{\mathbb{E}}[{\mathbf{1}}_\beta -{\mathbf{1}}^\alpha _{\beta }]\right ); \end{align}
\begin{align} \text{min}\! \left \{{1,\lambda ^{-1}}\right \}\left (\sum _{\alpha \in \Gamma }\pi _\alpha ^2 + \sum _{\alpha \in \Gamma }\sum _{\beta \in \Gamma ^+_\alpha } \pi _\alpha{\mathbb{E}}[{\mathbf{1}}^\alpha _{\beta }-{\mathbf{1}}_\beta ] + \sum _{\alpha \in \Gamma }\sum _{\beta \in \Gamma ^-_\alpha } \pi _\alpha{\mathbb{E}}[{\mathbf{1}}_\beta -{\mathbf{1}}^\alpha _{\beta }]\right ); \end{align}
noting that
![]() $\sum _{\beta \in \Gamma ^+_\alpha }{\mathbb{E}}[{\mathbf{1}}^\alpha _\beta -{\mathbf{1}}_\beta ]$
and
$\sum _{\beta \in \Gamma ^+_\alpha }{\mathbb{E}}[{\mathbf{1}}^\alpha _\beta -{\mathbf{1}}_\beta ]$
and
![]() $\sum _{\beta \in \Gamma ^-_\alpha } \pi _\alpha{\mathbb{E}}[{\mathbf{1}}_\beta -{\mathbf{1}}^\alpha _{\beta }]$
are, respectively, the expected gain and loss in the copies of
$\sum _{\beta \in \Gamma ^-_\alpha } \pi _\alpha{\mathbb{E}}[{\mathbf{1}}_\beta -{\mathbf{1}}^\alpha _{\beta }]$
are, respectively, the expected gain and loss in the copies of
![]() $H$
after forcing
$H$
after forcing
![]() $\alpha$
to be present in the graph
$\alpha$
to be present in the graph
![]() $G$
. We may simplify this further by omitting the negative terms in (5.2) and noting that, by (5.1),
$G$
. We may simplify this further by omitting the negative terms in (5.2) and noting that, by (5.1),
which yields the simpler (but somewhat larger) error bound
 \begin{align} \text{min}\! \left \{{1,\lambda ^{-1}}\right \}\left (\sum _{\alpha \in \Gamma }\pi _\alpha ^2 + \sum _{\alpha \in \Gamma }\sum _{\beta \in \Gamma ^+_\alpha }{\mathbb{E}}\left [{\mathbf{1}}_\alpha{\mathbf{1}}_\beta \right ] + \sum _{\alpha \in \Gamma }\sum _{\beta \in \Gamma ^-_\alpha } \pi _\alpha \pi _\beta \right ). \end{align}
\begin{align} \text{min}\! \left \{{1,\lambda ^{-1}}\right \}\left (\sum _{\alpha \in \Gamma }\pi _\alpha ^2 + \sum _{\alpha \in \Gamma }\sum _{\beta \in \Gamma ^+_\alpha }{\mathbb{E}}\left [{\mathbf{1}}_\alpha{\mathbf{1}}_\beta \right ] + \sum _{\alpha \in \Gamma }\sum _{\beta \in \Gamma ^-_\alpha } \pi _\alpha \pi _\beta \right ). \end{align}
As for Theorem4.2, the simplified error bound is the same as (5.2) or (5.4), but with the factor
![]() $\min \{1,\lambda ^{-1}\}$
replaced with
$\min \{1,\lambda ^{-1}\}$
replaced with
When applying Theorem4.3, we first sample a copy
![]() $K\in \Gamma$
of subgraph
$K\in \Gamma$
of subgraph
![]() $H$
with probabilities
$H$
with probabilities
![]() $\mathbb{P}(K=\alpha )$
proportional to
$\mathbb{P}(K=\alpha )$
proportional to
![]() ${\mathbb{E}}{\mathbf{1}}_\alpha$
, and construct the graphs
${\mathbb{E}}{\mathbf{1}}_\alpha$
, and construct the graphs
![]() $G^K$
and
$G^K$
and
![]() $G$
as above. The subgraph count
$G$
as above. The subgraph count
![]() $W$
and its size-bias version
$W$
and its size-bias version
![]() $W^s$
can then be found in
$W^s$
can then be found in
![]() $G$
and
$G$
and
![]() $G^K$
, respectively.
$G^K$
, respectively.
6. Proof of Theorem 3.11 and some useful lemmas
Here we prove some lemmas that are useful for proving the main results later. We also prove Theorem3.11 here, as some special cases of the result will be applied in the other proofs. To study the expected number of copies of a graph
![]() $H$
, we use the following definition. Let
$H$
, we use the following definition. Let
![]() $h$
be the number of vertices in
$h$
be the number of vertices in
![]() $H$
.
$H$
.
Definition 6.1 (Vertex marks and mark sequence). Let
![]() $\alpha$
be a potential copy of
$\alpha$
be a potential copy of
![]() $H$
and suppose that its vertices are
$H$
and suppose that its vertices are
![]() $k_1\lt \dots \lt k_h$
. We say that the mark of a vertex
$k_1\lt \dots \lt k_h$
. We say that the mark of a vertex
![]() $k_i\in \alpha$
is the out-degree of
$k_i\in \alpha$
is the out-degree of
![]() $k_i$
in
$k_i$
in
![]() $\alpha$
regarded as a directed graph (as always, with edges directed towards the smaller endpoint). The mark sequence is
$\alpha$
regarded as a directed graph (as always, with edges directed towards the smaller endpoint). The mark sequence is
![]() $(b_i)_{1\leqslant i\leqslant h}$
, with
$(b_i)_{1\leqslant i\leqslant h}$
, with
![]() $b_i$
being the mark of vertex
$b_i$
being the mark of vertex
![]() $k_i$
and for convenience, we occasionally refer to
$k_i$
and for convenience, we occasionally refer to
![]() $b_i=k$
as a k-mark.
$b_i=k$
as a k-mark.
In other words, for
![]() $\alpha$
to actually be a copy of
$\alpha$
to actually be a copy of
![]() $H$
in
$H$
in
![]() $G^m_n$
, there are for each
$G^m_n$
, there are for each
![]() $i\in [h]$
exactly
$i\in [h]$
exactly
![]() $b_i$
edges in
$b_i$
edges in
![]() $G^m_n$
from
$G^m_n$
from
![]() $k_i$
that have to have the endpoints determined by
$k_i$
that have to have the endpoints determined by
![]() $\alpha$
. Note that the mark sequence does not entirely encode the configuration of the copy of
$\alpha$
. Note that the mark sequence does not entirely encode the configuration of the copy of
![]() $H$
in
$H$
in
![]() $G^m_n$
, but, together with the sequence of vertices
$G^m_n$
, but, together with the sequence of vertices
![]() $k_i$
, the mark sequence gives the probability that the copy
$k_i$
, the mark sequence gives the probability that the copy
![]() $\alpha$
is present in
$\alpha$
is present in
![]() $G^m_n$
. In fact, since the edges in
$G^m_n$
. In fact, since the edges in
![]() $G^m_n$
choose their endpoints independently,
$G^m_n$
choose their endpoints independently,
 \begin{align} \pi _\alpha \,:\!=\, \mathbb{P}({\mathbf{1}}_\alpha =1) = \prod _{i=1}^h \frac{1}{(k_i-1)^{b_i}} = \prod _{i=2}^h \frac{1}{(k_i-1)^{b_i}}, \end{align}
\begin{align} \pi _\alpha \,:\!=\, \mathbb{P}({\mathbf{1}}_\alpha =1) = \prod _{i=1}^h \frac{1}{(k_i-1)^{b_i}} = \prod _{i=2}^h \frac{1}{(k_i-1)^{b_i}}, \end{align}
where the final equality holds because always
![]() $b_1=0$
, since edges are directed towards lower numbers, and thus
$b_1=0$
, since edges are directed towards lower numbers, and thus
![]() $\alpha$
has no out-edge from
$\alpha$
has no out-edge from
![]() $k_1$
. Similarly,
$k_1$
. Similarly,
![]() $b_h$
equals the degree of
$b_h$
equals the degree of
![]() $k_h$
in
$k_h$
in
![]() $\alpha$
, since
$\alpha$
, since
![]() $k_h$
has no in-edge.
$k_h$
has no in-edge.
Note that for a given unlabelled graph
![]() $H$
, there is a finite number (at most
$H$
, there is a finite number (at most
![]() $h!$
) of non-isomorphic labelled versions of
$h!$
) of non-isomorphic labelled versions of
![]() $H$
. Hence, in order to obtain estimates of the expected number of copies, it suffices to consider each possible labelled version separately, and then consider only potential copies with vertex sequences
$H$
. Hence, in order to obtain estimates of the expected number of copies, it suffices to consider each possible labelled version separately, and then consider only potential copies with vertex sequences
![]() $(k_i)_1^h$
where
$(k_i)_1^h$
where
![]() $k_1\lt \dots \lt k_h$
and
$k_1\lt \dots \lt k_h$
and
![]() $k_i$
corresponds to vertex
$k_i$
corresponds to vertex
![]() $i\in H$
. The mark sequence of the potential copy depends only on the labelled version of
$i\in H$
. The mark sequence of the potential copy depends only on the labelled version of
![]() $H$
. Different labelled versions of
$H$
. Different labelled versions of
![]() $H$
may yield different mark sequences
$H$
may yield different mark sequences
![]() $(b_i)_1^h$
, but they all have the same length
$(b_i)_1^h$
, but they all have the same length
![]() $h=v(H)$
, the number of vertices in
$h=v(H)$
, the number of vertices in
![]() $H$
, and the same sum
$H$
, and the same sum
 \begin{align} \sum _{i=1}^h b_i=e(H), \end{align}
\begin{align} \sum _{i=1}^h b_i=e(H), \end{align}
the number of edges in
![]() $H$
.
$H$
.
For the proof of Theorem 3.11, we also use the following definition.
Definition 6.2 (
![]() $F$
-number). We define the
$F$
-number). We define the
![]() $F$
-number,
$F$
-number,
![]() $F(a_i)$
of a finite sequence
$F(a_i)$
of a finite sequence
![]() $(a_i)$
of natural numbers as
$(a_i)$
of natural numbers as
![]() $\sum _{a_i\gt 1}a_i+\sum _{a_i=0}({-}2)$
, that is, we ignore all
$\sum _{a_i\gt 1}a_i+\sum _{a_i=0}({-}2)$
, that is, we ignore all
![]() $a_i$
with
$a_i$
with
![]() $a_i=1$
, count the
$a_i=1$
, count the
![]() $a_i$
with
$a_i$
with
![]() $a_i=0$
with weight
$a_i=0$
with weight
![]() $-2$
and count all other
$-2$
and count all other
![]() $a_i$
with
$a_i$
with
![]() $a_i$
as their weight.
$a_i$
as their weight.
Proof of Theorem
3.11. Consider a connected graph
![]() $H$
that is multicyclic and leaf-free, see Definition 3.10. Let
$H$
that is multicyclic and leaf-free, see Definition 3.10. Let
![]() $(b_i)_{1\leqslant i\leqslant h}$
be the mark sequence of a potential copy of
$(b_i)_{1\leqslant i\leqslant h}$
be the mark sequence of a potential copy of
![]() $H$
. By (6.1), the expected number of copies of
$H$
. By (6.1), the expected number of copies of
![]() $H$
with this mark sequence can be bounded by a constant times
$H$
with this mark sequence can be bounded by a constant times
 \begin{equation} S(b_1\cdots b_h)\,:\!=\, \sum _{1\leqslant k_1\lt \dots \lt k_h\lt \infty }\prod ^h_{i=2}\frac{1}{(k_i-1)^{b_i}}. \end{equation}
\begin{equation} S(b_1\cdots b_h)\,:\!=\, \sum _{1\leqslant k_1\lt \dots \lt k_h\lt \infty }\prod ^h_{i=2}\frac{1}{(k_i-1)^{b_i}}. \end{equation}
Hence it suffices to show that this infinite sum is finite for every mark sequence
![]() $(b_i)_1^h$
.
$(b_i)_1^h$
.
We will show this by modifying the mark sequence
![]() $(b_i)$
in such a way that preserves the sum in (6.2) and increases the sum
$(b_i)$
in such a way that preserves the sum in (6.2) and increases the sum
![]() $S(b_1\cdots b_h)$
in (6.3) until we reach a sequence where we can show that
$S(b_1\cdots b_h)$
in (6.3) until we reach a sequence where we can show that
![]() $S(b_1\cdots b_h)$
is finite. Note that we do not claim that the modified sequences actually are mark sequences for some copies of
$S(b_1\cdots b_h)$
is finite. Note that we do not claim that the modified sequences actually are mark sequences for some copies of
![]() $H$
; we consider the value
$H$
; we consider the value
![]() $S(b_1\cdots b_h)$
as defined by (6.3), without worrying about a probabilistic interpretation in general.
$S(b_1\cdots b_h)$
as defined by (6.3), without worrying about a probabilistic interpretation in general.
Since
![]() $H$
is leaf-free, each vertex in
$H$
is leaf-free, each vertex in
![]() $H$
has degree at least 2, and thus
$H$
has degree at least 2, and thus
![]() $b_h\gt 1$
. We change the sequence
$b_h\gt 1$
. We change the sequence
![]() $(b_i)_1^h$
as follows: In the first round, if
$(b_i)_1^h$
as follows: In the first round, if
![]() $b_h\gt 2$
and
$b_h\gt 2$
and
![]() $b_i=0$
for some
$b_i=0$
for some
![]() $i\neq 1$
, then decrease
$i\neq 1$
, then decrease
![]() $b_h$
by 1 and increase the last such
$b_h$
by 1 and increase the last such
![]() $b_i$
(i.e., the one with maximal
$b_i$
(i.e., the one with maximal
![]() $i$
) by 1. For instance,
$i$
) by 1. For instance,
![]() $0102023 \rightarrow 0102122$
. We repeat this process until
$0102023 \rightarrow 0102122$
. We repeat this process until
![]() $b_h=2$
or
$b_h=2$
or
![]() $b_i\gt 0$
for all
$b_i\gt 0$
for all
![]() $i\neq 1$
. In the second round, if
$i\neq 1$
. In the second round, if
![]() $b_h=2$
and
$b_h=2$
and
![]() $b_{h-1}\gt 1$
, then we repeat the same procedure with
$b_{h-1}\gt 1$
, then we repeat the same procedure with
![]() $b_{h-1}$
until
$b_{h-1}$
until
![]() $b_{h-1}=1$
or we have exhausted all
$b_{h-1}=1$
or we have exhausted all
![]() $b_i$
,
$b_i$
,
![]() $i\neq 1$
, such that
$i\neq 1$
, such that
![]() $b_i=0$
. Continue in the same way: in the
$b_i=0$
. Continue in the same way: in the
![]() $p$
th round (
$p$
th round (
![]() $3\leqslant p\lt h$
), if
$3\leqslant p\lt h$
), if
![]() $b_h=2$
,
$b_h=2$
,
![]() $b_{h-1}=\dots =b_{h-p+2}=1$
, and
$b_{h-1}=\dots =b_{h-p+2}=1$
, and
![]() $b_{h-p+1}\gt 1$
, then repeat the procedure for
$b_{h-p+1}\gt 1$
, then repeat the procedure for
![]() $b_{h-p+1}$
as we did for
$b_{h-p+1}$
as we did for
![]() $b_{h-1}$
. Stop when such moves are no longer possible. Denote the final sequence by
$b_{h-1}$
. Stop when such moves are no longer possible. Denote the final sequence by
![]() $(b^{\prime}_i)_1^h$
. We emphasise that these moves do not change the sum in (6.2) and never decrease
$(b^{\prime}_i)_1^h$
. We emphasise that these moves do not change the sum in (6.2) and never decrease
![]() $\prod ^h_{i=1}(k_i-1)^{-b_i}$
, since we always shift mass in the mark sequence to the left; thus
$\prod ^h_{i=1}(k_i-1)^{-b_i}$
, since we always shift mass in the mark sequence to the left; thus
![]() $S(b_1\cdots b_h)\leqslant S(b^{\prime}_1\cdots b^{\prime}_h)$
.
$S(b_1\cdots b_h)\leqslant S(b^{\prime}_1\cdots b^{\prime}_h)$
.
All the possible final sequences
![]() $(b^{\prime}_i)_1^h$
are analysed below:
$(b^{\prime}_i)_1^h$
are analysed below:
-
1. We have at least one intermediate zero left, say
 $b^{\prime}_q=0$
with
$b^{\prime}_q=0$
with
 $1\lt q\lt h$
and
$1\lt q\lt h$
and
 $q$
maximal among such indices. Then
$q$
maximal among such indices. Then
 $b^{\prime}_{q+1}=\dots =b^{\prime}_{h-1}=1$
and
$b^{\prime}_{q+1}=\dots =b^{\prime}_{h-1}=1$
and
 $b^{\prime}_h=2$
, since otherwise we would have modified the sequence further. In other words, we have a sequence of the form
$b^{\prime}_h=2$
, since otherwise we would have modified the sequence further. In other words, we have a sequence of the form
 $0XXX\cdots XXX011\cdots 112$
. This is not possible, due to the
$0XXX\cdots XXX011\cdots 112$
. This is not possible, due to the
 $F$
-number of the final part of the sequence
$F$
-number of the final part of the sequence
 $b^{\prime}_q\cdots b^{\prime}_h=0111\cdots 1112$
. Note that the moves that we made above cannot have affected
$b^{\prime}_q\cdots b^{\prime}_h=0111\cdots 1112$
. Note that the moves that we made above cannot have affected
 $b_i$
for
$b_i$
for
 $i\lt q$
, so they were entirely in this subsequence, and it is easy to see that each move either preserved or increased the
$i\lt q$
, so they were entirely in this subsequence, and it is easy to see that each move either preserved or increased the
 $F$
-number of this subsequence. Thus
$F$
-number of this subsequence. Thus
 $0=F(0111\cdots 1112)\geqslant F(b_{q}\cdots b_h)$
. with
$0=F(0111\cdots 1112)\geqslant F(b_{q}\cdots b_h)$
. with
 $(b_i)_{1\leqslant i\leqslant h}$
being the original mark sequence. A way of interpreting the
$(b_i)_{1\leqslant i\leqslant h}$
being the original mark sequence. A way of interpreting the
 $F$
-number is as an upper bound of the number of edges directed from the last
$F$
-number is as an upper bound of the number of edges directed from the last
 $h-q+1$
nodes to the first
$h-q+1$
nodes to the first
 $q-1$
nodes, which equals the sum of the differences between outdegree and indegree for the last
$q-1$
nodes, which equals the sum of the differences between outdegree and indegree for the last
 $h-q+1$
nodes. In any copy of a connected graph
$h-q+1$
nodes. In any copy of a connected graph
 $H$
that is multicyclic and leaf-free, a vertex with mark
$H$
that is multicyclic and leaf-free, a vertex with mark
 $0$
must receive at least
$0$
must receive at least
 $2$
in-edges and thus contributes at most
$2$
in-edges and thus contributes at most
 $a_i=-2$
to the count. A vertex
$a_i=-2$
to the count. A vertex
 $i$
with mark
$i$
with mark
 $1$
sends one edge but receives at least
$1$
sends one edge but receives at least
 $1$
, and so contributes at most
$1$
, and so contributes at most
 $a_i=0$
to the count. Similarly, a vertex
$a_i=0$
to the count. Similarly, a vertex
 $i$
with mark
$i$
with mark
 $k\gt 1$
may receive some in-edges and so contributes at most
$k\gt 1$
may receive some in-edges and so contributes at most
 $a_i=k$
to the count. Since
$a_i=k$
to the count. Since
 $H$
is a connected graph, we must have some edge connecting the last
$H$
is a connected graph, we must have some edge connecting the last
 $h-q+1$
vertices and the first
$h-q+1$
vertices and the first
 $q-1$
vertices in
$q-1$
vertices in
 $H$
, and so
$H$
, and so
 $F( b_{q}\cdots b_h)\gt 0$
, contradicting the above.
$F( b_{q}\cdots b_h)\gt 0$
, contradicting the above. -
2. We have removed all the zeroes (except the first) and ended up with
 $0XX\cdots XX b^{\prime}_h$
where
$0XX\cdots XX b^{\prime}_h$
where
 $b^{\prime}_h\gt 2$
and each
$b^{\prime}_h\gt 2$
and each
 $X$
is at least
$X$
is at least
 $1$
. (In this case, we could not reduce the last number down to 2 before running out of zeroes.) The sequence can be compared to the sequence
$1$
. (In this case, we could not reduce the last number down to 2 before running out of zeroes.) The sequence can be compared to the sequence
 $0111\cdots 1113$
which gives a larger or equal value of (6.3). For the latter sequence we have, if
$0111\cdots 1113$
which gives a larger or equal value of (6.3). For the latter sequence we have, if
 $h\ge 3$
, by first summing over
$h\ge 3$
, by first summing over
 $k_h\gt k_{h-1}$
,(6.4)which is the same sum with
$k_h\gt k_{h-1}$
,(6.4)which is the same sum with \begin{align} S(011\cdots 113)&= \sum _{1\leqslant k_1\lt \dots \lt k_h}\prod ^{h-1}_{i=2}\frac{1}{k_i-1}\cdot \frac{1}{(k_h-1)^3} \notag \\& \leqslant \sum _{1\leqslant k_1\lt \dots \lt k_{h-1}}\prod ^{h-2}_{i=2}\frac{1}{k_i-1}\cdot \frac{1}{(k_{h-1}-1)^3}, \end{align}
\begin{align} S(011\cdots 113)&= \sum _{1\leqslant k_1\lt \dots \lt k_h}\prod ^{h-1}_{i=2}\frac{1}{k_i-1}\cdot \frac{1}{(k_h-1)^3} \notag \\& \leqslant \sum _{1\leqslant k_1\lt \dots \lt k_{h-1}}\prod ^{h-2}_{i=2}\frac{1}{k_i-1}\cdot \frac{1}{(k_{h-1}-1)^3}, \end{align}
 $h$
replaced by
$h$
replaced by
 $h-1$
; thus induction yields(6.5)
$h-1$
; thus induction yields(6.5) \begin{align} S(011\cdots 113)\leqslant S(03)= \sum _{1\leqslant k_1\lt k_2}\frac{1}{(k_2-1)^3} = \sum _{k_2\ge 2}\frac{1}{(k_2-1)^2}\lt \infty . \end{align}
\begin{align} S(011\cdots 113)\leqslant S(03)= \sum _{1\leqslant k_1\lt k_2}\frac{1}{(k_2-1)^3} = \sum _{k_2\ge 2}\frac{1}{(k_2-1)^2}\lt \infty . \end{align}
-
3. We have
 $0XXX\cdots XXX2$
where the
$0XXX\cdots XXX2$
where the
 $X$
’s are at least 1. In this case, note that not all the
$X$
’s are at least 1. In this case, note that not all the
 $X$
’s can be 1, as
$X$
’s can be 1, as
 $H$
for topological reasons has more edges than vertices. Thus at least one
$H$
for topological reasons has more edges than vertices. Thus at least one
 $X$
is at least
$X$
is at least
 $2$
. If
$2$
. If
 $b^{\prime}_2=1$
, we can exchange
$b^{\prime}_2=1$
, we can exchange
 $b^{\prime}_2$
with
$b^{\prime}_2$
with
 $b^{\prime}_j$
for some
$b^{\prime}_j$
for some
 $j\lt h$
such that
$j\lt h$
such that
 $b^{\prime}_j\gt 1$
, again without decreasing
$b^{\prime}_j\gt 1$
, again without decreasing
 $S$
. We can then compare the sequence to
$S$
. We can then compare the sequence to
 $02111\cdots 1112$
. By arguing as in (6.4)–(6.5), we find(6.6)
$02111\cdots 1112$
. By arguing as in (6.4)–(6.5), we find(6.6) \begin{align} S(0211\cdots 112)& \leqslant S(022) =\sum _{1\leqslant k_1\lt k_2\lt k_3}\frac{1}{(k_2-1)^2(k_3-1)^2} \notag \\& \leqslant \sum _{1\leqslant k_1\lt k_2}\frac{1}{(k_2-1)^3}=S(03)\lt \infty . \end{align}
\begin{align} S(0211\cdots 112)& \leqslant S(022) =\sum _{1\leqslant k_1\lt k_2\lt k_3}\frac{1}{(k_2-1)^2(k_3-1)^2} \notag \\& \leqslant \sum _{1\leqslant k_1\lt k_2}\frac{1}{(k_2-1)^3}=S(03)\lt \infty . \end{align}
This completes the proof of the theorem.
For the expected number of
![]() $\ell$
-cycles, which is not covered by Theorem3.11, we use a simpler version of the argument above to prove the following lemma, which essentially says that it is enough to just consider one particular configuration of an
$\ell$
-cycles, which is not covered by Theorem3.11, we use a simpler version of the argument above to prove the following lemma, which essentially says that it is enough to just consider one particular configuration of an
![]() $\ell$
-cycle. We first observe that in the mark sequence of a potential copy of a cycle, all marks are 0, 1, or 2; furthermore, there must be equal numbers of 0-marks and 2-marks by (6.2). An
$\ell$
-cycle. We first observe that in the mark sequence of a potential copy of a cycle, all marks are 0, 1, or 2; furthermore, there must be equal numbers of 0-marks and 2-marks by (6.2). An
![]() $\ell$
-cycle has
$\ell$
-cycle has
![]() $\ell$
marks. As noted above, we must have
$\ell$
marks. As noted above, we must have
![]() $b_1=0$
and
$b_1=0$
and
![]() $b_\ell =2$
, since edges are directed towards lower numbers. Note that an
$b_\ell =2$
, since edges are directed towards lower numbers. Note that an
![]() $\ell$
-cycle has at most
$\ell$
-cycle has at most
![]() $\lfloor{\ell /2}\rfloor$
vertices of mark 0.
$\lfloor{\ell /2}\rfloor$
vertices of mark 0.
Lemma 6.3.
Among all potential copies of an
![]() $\ell$
-cycle on given vertices
$\ell$
-cycle on given vertices
![]() $k_1\lt \dots \lt k_\ell$
, the configurations with the mark sequence
$k_1\lt \dots \lt k_\ell$
, the configurations with the mark sequence
![]() $011\cdots 112$
have the largest probability to occur in
$011\cdots 112$
have the largest probability to occur in
![]() $G^m_n$
.
$G^m_n$
.
Proof. In a cycle, if a vertex sends
![]() $j$
edges, it receives
$j$
edges, it receives
![]() $2-j$
edges. Consider the mark sequence
$2-j$
edges. Consider the mark sequence
![]() $(b_i)_1^\ell$
of a potential copy of an
$(b_i)_1^\ell$
of a potential copy of an
![]() $\ell$
-cycle. Since the F-number of the sequence of the last
$\ell$
-cycle. Since the F-number of the sequence of the last
![]() $k\leqslant \ell$
marks must be positive (by the earlier argument for proving Theorem3.11), the number of 2-marks must always be larger than the number of 0-marks, except when
$k\leqslant \ell$
marks must be positive (by the earlier argument for proving Theorem3.11), the number of 2-marks must always be larger than the number of 0-marks, except when
![]() $k=\ell$
, in which case they are equal. Equivalently,
$k=\ell$
, in which case they are equal. Equivalently,
 \begin{align} \sum _{\ell -k+1}^\ell (b_i-1)\geqslant 0, \text{with strict inequality when $1\leqslant k\lt \ell $}. \end{align}
\begin{align} \sum _{\ell -k+1}^\ell (b_i-1)\geqslant 0, \text{with strict inequality when $1\leqslant k\lt \ell $}. \end{align}
This holds since the cycle is connected, and so the total number of out-edges of the last
![]() $k$
vertices must be larger than their total number of in-edges when
$k$
vertices must be larger than their total number of in-edges when
![]() $k\lt \ell$
(
$k\lt \ell$
(
![]() $k=\ell$
gives equality). The probability of the cycle appearing in
$k=\ell$
gives equality). The probability of the cycle appearing in
![]() $G^m_n$
is given by (6.1). Consider all sequences
$G^m_n$
is given by (6.1). Consider all sequences
![]() $(b_i)_1^\ell$
with
$(b_i)_1^\ell$
with
![]() $b_i\in{\{0,1,2\}}$
such that (6.7) holds. We must have
$b_i\in{\{0,1,2\}}$
such that (6.7) holds. We must have
![]() $b_1=0$
and
$b_1=0$
and
![]() $b_\ell =2$
. If there is another mark
$b_\ell =2$
. If there is another mark
![]() $b_j=2$
with
$b_j=2$
with
![]() $j\neq \ell$
in the sequence, let
$j\neq \ell$
in the sequence, let
![]() $j$
be the largest such index. Then there must also be an index
$j$
be the largest such index. Then there must also be an index
![]() $i\neq 1$
with
$i\neq 1$
with
![]() $b_i=0$
; let
$b_i=0$
; let
![]() $i$
be the largest such index. We must have
$i$
be the largest such index. We must have
![]() $i\lt j$
, since otherwise (6.7) would be violated for
$i\lt j$
, since otherwise (6.7) would be violated for
![]() $k=\ell -i+1$
. It is then easy to see that if we change both
$k=\ell -i+1$
. It is then easy to see that if we change both
![]() $b_i$
and
$b_i$
and
![]() $b_j$
to 1, then (6.7) still holds, and the value of (6.1) is increased. Consequently, the mark sequence with the largest probability is of the form
$b_j$
to 1, then (6.7) still holds, and the value of (6.1) is increased. Consequently, the mark sequence with the largest probability is of the form
![]() $0111\cdots 1112$
.
$0111\cdots 1112$
.
The lemma below concerns trees and is used when we prove the normal approximation results.
Lemma 6.4.
Fix the positive integer
![]() $t$
and let
$t$
and let
![]() $\mathcal{T}$
be a rooted tree with
$\mathcal{T}$
be a rooted tree with
![]() $t$
edges and thus
$t$
edges and thus
![]() $t+1$
vertices. The following results concerning
$t+1$
vertices. The following results concerning
![]() $\mathcal{T}$
hold.
$\mathcal{T}$
hold.
-
(i) Among all potential copies of
 $\mathcal{T}$
on a given vertex set, the configurations with the mark sequence
$\mathcal{T}$
on a given vertex set, the configurations with the mark sequence
 $011\cdots 11$
have the largest probability.
$011\cdots 11$
have the largest probability.
-
(ii) Let
 $N_x$
be the number of copies of
$N_x$
be the number of copies of
 $\mathcal{T}$
with vertex
$\mathcal{T}$
with vertex
 $x$
as its distinguished root. Then
$x$
as its distinguished root. Then
 ${\mathbb{E}} N_x=O(\log ^{t}n)$
, uniformly for
${\mathbb{E}} N_x=O(\log ^{t}n)$
, uniformly for
 $1\leqslant x\leqslant n\lt \infty$
.
$1\leqslant x\leqslant n\lt \infty$
.
Proof. 1: Let
![]() $0b_2\cdots b_{t+1}$
be the mark sequence of a potential copy of
$0b_2\cdots b_{t+1}$
be the mark sequence of a potential copy of
![]() $\mathcal{T}$
. Note first that if
$\mathcal{T}$
. Note first that if
![]() $2\leqslant k\leqslant t+1$
, then we have, summing over the
$2\leqslant k\leqslant t+1$
, then we have, summing over the
![]() $t+2-k$
last vertices,
$t+2-k$
last vertices,
 \begin{align} \sum _{i=k}^{t+1}b_i\geqslant t+2-k. \end{align}
\begin{align} \sum _{i=k}^{t+1}b_i\geqslant t+2-k. \end{align}
In fact, this sum is the number of edges with upper endpoint in
![]() $[k,t+1]$
, which equals the number of edges with at least one endpoint in
$[k,t+1]$
, which equals the number of edges with at least one endpoint in
![]() $[k,t+1]$
, and in any connected graph, a proper subset of
$[k,t+1]$
, and in any connected graph, a proper subset of
![]() $\ell$
vertices is always adjacent to at least
$\ell$
vertices is always adjacent to at least
![]() $\ell$
edges. (To see this, collapse all other vertices into one and pick a spanning tree with
$\ell$
edges. (To see this, collapse all other vertices into one and pick a spanning tree with
![]() $\ell$
edges in the resulting graph.)
$\ell$
edges in the resulting graph.)
We argue similarly to the proof of Theorem 3.11, now modifing the mark sequence as follows. As long as some
![]() $b_i\ge 2$
, we reduce the rightmost such
$b_i\ge 2$
, we reduce the rightmost such
![]() $b_i$
by 1 and increase the rightmost mark 0 to 1. We can never reach a sequence ending with a proper subsequence
$b_i$
by 1 and increase the rightmost mark 0 to 1. We can never reach a sequence ending with a proper subsequence
![]() $011\cdots 11$
with some
$011\cdots 11$
with some
![]() $b_k=0$
(
$b_k=0$
(
![]() $k\ge 2$
) and
$k\ge 2$
) and
![]() $b_{k+1}=\dots =b_{t+1}=1$
, because the first time this happens, all previous moves must have been inside
$b_{k+1}=\dots =b_{t+1}=1$
, because the first time this happens, all previous moves must have been inside
![]() $[k,\dots, t+1]$
, so the sum in (6.8) has not changed and (6.8) still holds, a contradiction. Consequently, we do not stop until there is no mark 0 except
$[k,\dots, t+1]$
, so the sum in (6.8) has not changed and (6.8) still holds, a contradiction. Consequently, we do not stop until there is no mark 0 except
![]() $b_1$
, but since the sum of all marks is
$b_1$
, but since the sum of all marks is
![]() $t$
by (6.2) (and this sum is not changed), the final sequence is
$t$
by (6.2) (and this sum is not changed), the final sequence is
![]() $011\cdots 11$
. As the procedure never decreases the probability (6.1), the mark sequence
$011\cdots 11$
. As the procedure never decreases the probability (6.1), the mark sequence
![]() $011\cdots 11$
indeed yields the largest probability.
$011\cdots 11$
indeed yields the largest probability.
2: We use 1 to obtain
 \begin{align}{\mathbb{E}} N_x& \leqslant C\left (\sum _{x\lt k_1\lt \dots \lt k_{t}\leqslant n}\prod ^{t}_{i=1}\frac{1}{k_i} + \sum ^{t}_{r=1}\sum _{k_1\lt \dots \lt k_r\lt x\lt k_{r+1}\lt \dots \lt k_{t}\leqslant n} \frac{1}{x}\prod ^{t}_{i=2}\frac{1}{k_i}\right ) \notag \\& \leqslant C\left (\sum _{x\lt k_1\lt \dots \lt k_{t}\leqslant n}\prod ^{t}_{i=1}\frac{1}{k_i} + \sum ^{t}_{r=1}\sum _{k_1\lt \dots \lt k_r\lt x\lt k_{r+1}\lt \dots \lt k_{t}\leqslant n} \prod ^{t}_{i=1}\frac{1}{k_i}\right ) \notag \\& \leqslant C \prod ^{t}_{i=1}\sum _{k_i=1}^n\frac{1}{k_i} \leqslant C\bigl (\log n+1\bigr )^t, \end{align}
\begin{align}{\mathbb{E}} N_x& \leqslant C\left (\sum _{x\lt k_1\lt \dots \lt k_{t}\leqslant n}\prod ^{t}_{i=1}\frac{1}{k_i} + \sum ^{t}_{r=1}\sum _{k_1\lt \dots \lt k_r\lt x\lt k_{r+1}\lt \dots \lt k_{t}\leqslant n} \frac{1}{x}\prod ^{t}_{i=2}\frac{1}{k_i}\right ) \notag \\& \leqslant C\left (\sum _{x\lt k_1\lt \dots \lt k_{t}\leqslant n}\prod ^{t}_{i=1}\frac{1}{k_i} + \sum ^{t}_{r=1}\sum _{k_1\lt \dots \lt k_r\lt x\lt k_{r+1}\lt \dots \lt k_{t}\leqslant n} \prod ^{t}_{i=1}\frac{1}{k_i}\right ) \notag \\& \leqslant C \prod ^{t}_{i=1}\sum _{k_i=1}^n\frac{1}{k_i} \leqslant C\bigl (\log n+1\bigr )^t, \end{align}
which completes the proof.
7. Proof of the Poisson approximations for cycles
In this section we prove the Poisson approximation results in Theorems3.1 and 3.3 using Theorems3.11, 4.1 and 4.2. We fix in this section the integers
![]() $m\ge 1$
and
$m\ge 1$
and
![]() $\ell \ge 2$
and denote by
$\ell \ge 2$
and denote by
![]() $W_n$
the count of
$W_n$
the count of
![]() $\ell$
-cycles in
$\ell$
-cycles in
![]() $G^m_n$
.
$G^m_n$
.
Proof of Theorems
3.1 and 3.3. We start by proving the result on the expected number of cycles
![]() $\mu _n$
in (3.1). By Lemma 6.3 and (6.1),
$\mu _n$
in (3.1). By Lemma 6.3 and (6.1),
![]() $\mu _n$
can be bounded above by
$\mu _n$
can be bounded above by
 \begin{align} \psi _{\ell, m}\sum _{k_1\lt \dots \lt k_\ell \leqslant n}\frac{1}{(k_\ell -1)^2}\prod ^{\ell -1}_{i=2}\frac{1}{k_i-1}, \end{align}
\begin{align} \psi _{\ell, m}\sum _{k_1\lt \dots \lt k_\ell \leqslant n}\frac{1}{(k_\ell -1)^2}\prod ^{\ell -1}_{i=2}\frac{1}{k_i-1}, \end{align}
where
![]() $\psi _{\ell, m}$
is the total number of ways of forming a potential
$\psi _{\ell, m}$
is the total number of ways of forming a potential
![]() $\ell$
-cycle on
$\ell$
-cycle on
![]() $\ell$
given vertices. Summing over
$\ell$
given vertices. Summing over
![]() $k_1,\dots, k_{\ell -1}$
(in this order), the above is at most
$k_1,\dots, k_{\ell -1}$
(in this order), the above is at most
![]() $\psi _{\ell, m}\sum ^n_{k_\ell =\ell }\frac{1}{k_\ell -1}$
, which can be bounded by
$\psi _{\ell, m}\sum ^n_{k_\ell =\ell }\frac{1}{k_\ell -1}$
, which can be bounded by
![]() $\psi _{\ell, m} (\log n+1)$
. The calculation for the lower bound is similar, with the factor
$\psi _{\ell, m} (\log n+1)$
. The calculation for the lower bound is similar, with the factor
![]() $\psi _{\ell, m}$
replaced by 1; we consider just one configuration that has mark sequence
$\psi _{\ell, m}$
replaced by 1; we consider just one configuration that has mark sequence
![]() $011\cdots 11$
.
$011\cdots 11$
.
Next, we construct the size-bias coupling of the cycle count described in Section 5. To prove the approximation result in Theorem3.1, it then suffices to show that the sums in (5.4) are bounded as
![]() $n\to \infty$
; the error bound then follows from (5.4) and (3.1).
$n\to \infty$
; the error bound then follows from (5.4) and (3.1).
Let
![]() $\Gamma$
be the set of potential cycles and let as in (6.1)
$\Gamma$
be the set of potential cycles and let as in (6.1)
![]() $\pi _\alpha$
be the probability of cycle
$\pi _\alpha$
be the probability of cycle
![]() $\alpha \in \Gamma$
being a subgraph of
$\alpha \in \Gamma$
being a subgraph of
![]() $G^m_n$
. By (6.1) and Lemma 6.3, using the notation (6.3),
$G^m_n$
. By (6.1) and Lemma 6.3, using the notation (6.3),
 \begin{align} \sum _{\alpha \in \Gamma }\pi _\alpha ^2\leqslant C\sum _{k_1\lt \dots \lt k_\ell \leqslant n}k^{-4}_\ell \prod ^{\ell -1}_{i=2}k^{-2}_i \leqslant C\cdot S(022\cdots 224) \leqslant C \cdot S(011\cdots 113), \end{align}
\begin{align} \sum _{\alpha \in \Gamma }\pi _\alpha ^2\leqslant C\sum _{k_1\lt \dots \lt k_\ell \leqslant n}k^{-4}_\ell \prod ^{\ell -1}_{i=2}k^{-2}_i \leqslant C\cdot S(022\cdots 224) \leqslant C \cdot S(011\cdots 113), \end{align}
which is finite by (6.5).
In the sum
each term
![]() ${\mathbb{E}}[{\mathbf{1}}_\alpha{\mathbf{1}}_\beta ]=\mathbb{P}[{\mathbf{1}}_\alpha{\mathbf{1}}_\beta =1]$
is the probability that
${\mathbb{E}}[{\mathbf{1}}_\alpha{\mathbf{1}}_\beta ]=\mathbb{P}[{\mathbf{1}}_\alpha{\mathbf{1}}_\beta =1]$
is the probability that
![]() $G^m_n$
contains a specific copy of a graph
$G^m_n$
contains a specific copy of a graph
![]() $H$
obtained by merging the cycles
$H$
obtained by merging the cycles
![]() $\alpha$
and
$\alpha$
and
![]() $\beta$
. See Figure 3 for an illustration. There is only a finite number of such graphs
$\beta$
. See Figure 3 for an illustration. There is only a finite number of such graphs
![]() $H$
(up to isomorphism); each copy of a graph
$H$
(up to isomorphism); each copy of a graph
![]() $H$
arises for a bounded number of pairs
$H$
arises for a bounded number of pairs
![]() $(\alpha, \beta )$
; and each such graph
$(\alpha, \beta )$
; and each such graph
![]() $H$
is connected, multicyclic and leaf-free (see Definition 3.10). Consequently, the sum (7.3) is bounded by a constant times the sum of the expected number of copies of such graphs
$H$
is connected, multicyclic and leaf-free (see Definition 3.10). Consequently, the sum (7.3) is bounded by a constant times the sum of the expected number of copies of such graphs
![]() $H$
, and Theorem3.11 shows that this sum is bounded as
$H$
, and Theorem3.11 shows that this sum is bounded as
![]() $n\to \infty$
.
$n\to \infty$
.
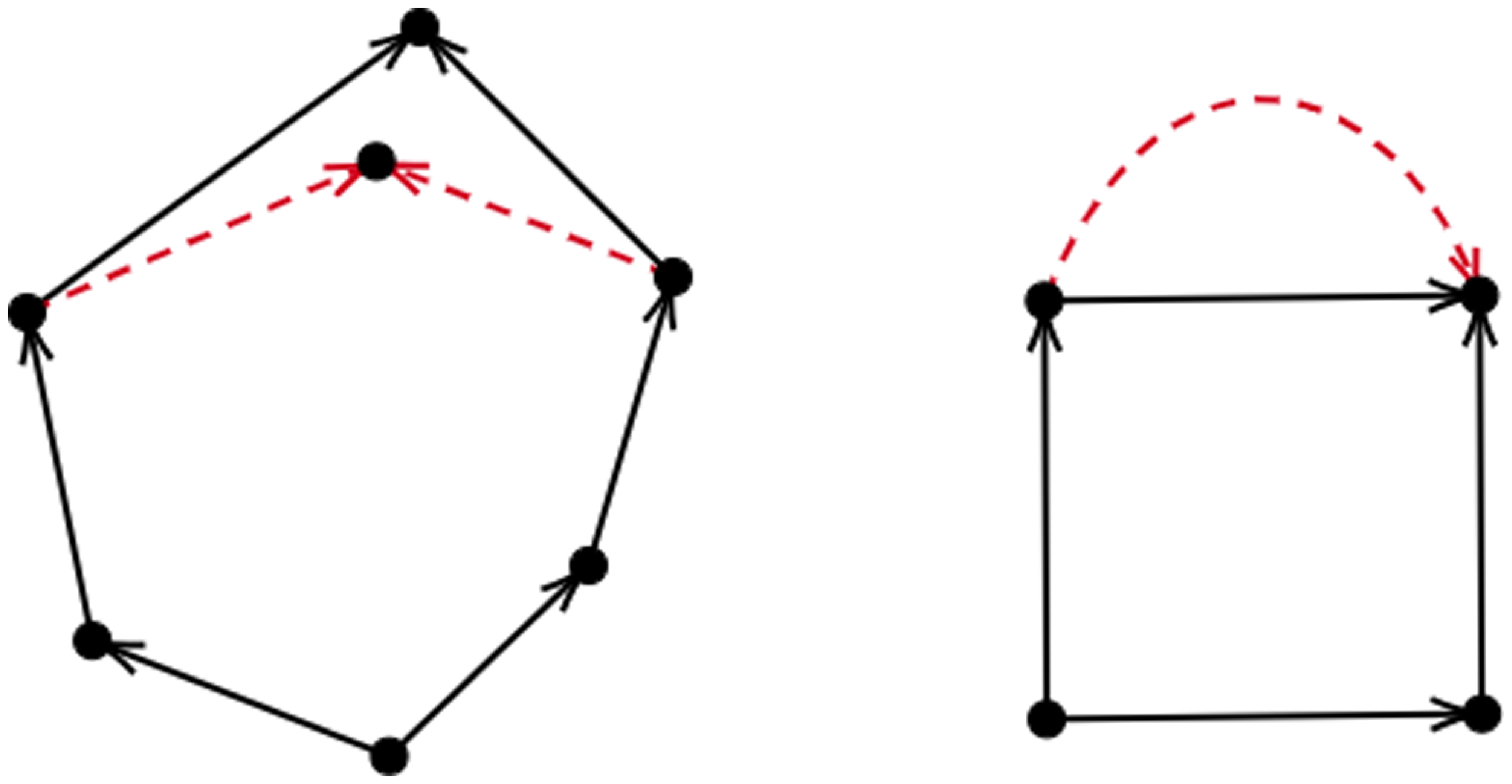
Figure 3. Two examples of positively correlated cycles. In each example, the red dashed edges form the additional segment that gives rise to the other cycle.
Finally, note that if
![]() $\beta \in \Gamma ^-_\alpha$
, then the cycles
$\beta \in \Gamma ^-_\alpha$
, then the cycles
![]() $\alpha$
and
$\alpha$
and
![]() $\beta$
have at least one common vertex. Consider a uniform attachment graph
$\beta$
have at least one common vertex. Consider a uniform attachment graph
![]() $G^{2m}_n$
where the first
$G^{2m}_n$
where the first
![]() $m$
out-edges of any vertex
$m$
out-edges of any vertex
![]() $2\leqslant i\leqslant n$
are coloured red, and the remaining
$2\leqslant i\leqslant n$
are coloured red, and the remaining
![]() $m$
out-edges of these vertices are coloured blue. This graph can be thought of as overlaying two independent copies of
$m$
out-edges of these vertices are coloured blue. This graph can be thought of as overlaying two independent copies of
![]() $G^{m}_n$
. Let
$G^{m}_n$
. Let
![]() $\alpha{\cdot }\beta$
be the subgraph of
$\alpha{\cdot }\beta$
be the subgraph of
![]() $K^{2m}_n$
obtained by regarding
$K^{2m}_n$
obtained by regarding
![]() $\alpha$
and
$\alpha$
and
![]() $\beta$
living in the red and blue parts, respectively, and taking the union of them. (Thus, the
$\beta$
living in the red and blue parts, respectively, and taking the union of them. (Thus, the
![]() $i$
-th edge of vertex
$i$
-th edge of vertex
![]() $j$
,
$j$
,
![]() $j^{(i)}$
, that is part of
$j^{(i)}$
, that is part of
![]() $\beta$
is now written as
$\beta$
is now written as
![]() $j^{(i+m)}$
.) With some slight abuse of notation, let
$j^{(i+m)}$
.) With some slight abuse of notation, let
![]() ${\mathbf{1}}_{\alpha{\cdot }\beta }$
be the indicator of the subgraph
${\mathbf{1}}_{\alpha{\cdot }\beta }$
be the indicator of the subgraph
![]() $\alpha{\cdot }\beta$
in
$\alpha{\cdot }\beta$
in
![]() $G^{2m}_n$
. By the edge independence, we have
$G^{2m}_n$
. By the edge independence, we have
![]() $\pi _\alpha \pi _{\beta }={\mathbb{E}}{\mathbf{1}}_{\alpha{\cdot }\beta }$
, which is the probability that
$\pi _\alpha \pi _{\beta }={\mathbb{E}}{\mathbf{1}}_{\alpha{\cdot }\beta }$
, which is the probability that
![]() $G^{2m}_n$
contains a given copy of a graph
$G^{2m}_n$
contains a given copy of a graph
![]() $H$
that, just as in the argument for
$H$
that, just as in the argument for
![]() $\Gamma ^+_\alpha$
, is obtained by merging the cycles
$\Gamma ^+_\alpha$
, is obtained by merging the cycles
![]() $\alpha$
and
$\alpha$
and
![]() $\beta$
. There is only a finite number of such graphs
$\beta$
. There is only a finite number of such graphs
![]() $H$
, so it follows from Theorem3.11 that the expected number of copies of any of them in
$H$
, so it follows from Theorem3.11 that the expected number of copies of any of them in
![]() $G^{2m}_n$
is bounded as
$G^{2m}_n$
is bounded as
![]() $n\to \infty$
, and thus
$n\to \infty$
, and thus
This completes the proof of Theorem3.1.
The proof of Theorem3.3 is similar, using Theorem4.2; we now have
![]() $\Gamma =\bigcup _{j=1}^r\Gamma _j$
, where
$\Gamma =\bigcup _{j=1}^r\Gamma _j$
, where
![]() $\Gamma _j$
is the set of potential
$\Gamma _j$
is the set of potential
![]() $\ell (j)$
-cycles. We estimate (7.2)–(7.4) as above, when necessary replacing
$\ell (j)$
-cycles. We estimate (7.2)–(7.4) as above, when necessary replacing
![]() $\ell$
by
$\ell$
by
![]() $\ell (j)$
and summing over
$\ell (j)$
and summing over
![]() $j=1,\dots, r$
.
$j=1,\dots, r$
.
8. Proof of the normal approximation for unicyclic graphs
8.1 Proofs of (3.12) and (3.19)
We first prove (3.12) in Theorem 3.5 and (3.19) in Theorem3.13, which have similar proofs.
Proof of
(3.12). Given a potential
![]() $\ell$
-cycle
$\ell$
-cycle
![]() $\alpha$
, let
$\alpha$
, let
![]() $\Xi (\alpha )$
be the set of
$\Xi (\alpha )$
be the set of
![]() $s$
-tuples
$s$
-tuples
![]() $(\beta _1,\dots, \beta _s)$
of potential copies of
$(\beta _1,\dots, \beta _s)$
of potential copies of
![]() $\mathcal{T}_i$
,
$\mathcal{T}_i$
,
![]() $i=1,\dots, s$
, that can be added to
$i=1,\dots, s$
, that can be added to
![]() $\alpha$
to form a potential copy of
$\alpha$
to form a potential copy of
![]() $\Lambda$
. Denote by
$\Lambda$
. Denote by
![]() $\Gamma _{\mathrm{cycle}}$
the set of potential
$\Gamma _{\mathrm{cycle}}$
the set of potential
![]() $\ell$
-cycles. By independence of the edges, (3.1) and Lemma 6.4(ii), we have
$\ell$
-cycles. By independence of the edges, (3.1) and Lemma 6.4(ii), we have
noting that in the inequality we have used the assumption that
![]() $\ell$
and
$\ell$
and
![]() $\mathcal{T}_i$
,
$\mathcal{T}_i$
,
![]() $i=1,\dots, s$
, are fixed.
$i=1,\dots, s$
, are fixed.
For the lower bound on
![]() $\mu _n$
, we choose a suitable configuration on a set of vertices
$\mu _n$
, we choose a suitable configuration on a set of vertices
![]() $k_1\lt \dots \lt k_{\ell +t}$
. We use
$k_1\lt \dots \lt k_{\ell +t}$
. We use
![]() $k_1\lt \dots \lt k_\ell$
to form a cycle whose configuration has the mark sequence
$k_1\lt \dots \lt k_\ell$
to form a cycle whose configuration has the mark sequence
![]() $011\cdots 112$
, and
$011\cdots 112$
, and
![]() $k_{\ell +1}\lt \dots \lt k_{\ell +t}$
to construct the trees
$k_{\ell +1}\lt \dots \lt k_{\ell +t}$
to construct the trees
![]() $(\mathcal{T}_i)_{1\leqslant i\leqslant s}$
, taking their vertices in some order going from the roots outwards, so that each non-root vertex in
$(\mathcal{T}_i)_{1\leqslant i\leqslant s}$
, taking their vertices in some order going from the roots outwards, so that each non-root vertex in
![]() $\mathcal{T}_i$
has mark 1; this gives a potential copy of
$\mathcal{T}_i$
has mark 1; this gives a potential copy of
![]() $\Lambda$
with all 1-marks except
$\Lambda$
with all 1-marks except
![]() $b_1=0$
and
$b_1=0$
and
![]() $b_\ell =2$
. Hence
$b_\ell =2$
. Hence
![]() $\mu _n$
is at least, for some constant
$\mu _n$
is at least, for some constant
![]() $c\gt 0$
, by first summing iteratively over
$c\gt 0$
, by first summing iteratively over
![]() $k_1\lt \dots \lt k_{\ell -1}$
,
$k_1\lt \dots \lt k_{\ell -1}$
,
 \begin{align} \sum _{k_1\lt \dots \lt k_{\ell +t}\leqslant n}\frac{1}{(k_2-1)\cdots (k_{\ell -1}-1)(k_\ell -1)^2}\prod ^{\ell +t}_{i=\ell +1} \frac{1}{k_i-1} &\geqslant c\sum _{\ell \leqslant k_\ell \lt \dots \lt k_{\ell +t}\leqslant n} \prod ^{\ell +t}_{i=\ell } \frac{1}{k_i-1}\\ &=\Theta \bigl (\log ^{t+1}n\bigr ),\nonumber \end{align}
\begin{align} \sum _{k_1\lt \dots \lt k_{\ell +t}\leqslant n}\frac{1}{(k_2-1)\cdots (k_{\ell -1}-1)(k_\ell -1)^2}\prod ^{\ell +t}_{i=\ell +1} \frac{1}{k_i-1} &\geqslant c\sum _{\ell \leqslant k_\ell \lt \dots \lt k_{\ell +t}\leqslant n} \prod ^{\ell +t}_{i=\ell } \frac{1}{k_i-1}\\ &=\Theta \bigl (\log ^{t+1}n\bigr ),\nonumber \end{align}
as required.
8.2 Proofs of variance estimates
We next prove the variance estimates (3.13) in Theorem 3.5 and (3.20) in Theorem3.13.
Proof of
(3.13). Recall that a connected unicyclic graph
![]() $\Lambda$
can be constructed as follows. Let
$\Lambda$
can be constructed as follows. Let
![]() $\mathcal{C}_\ell$
be an
$\mathcal{C}_\ell$
be an
![]() $\ell$
-cycle and let
$\ell$
-cycle and let
![]() $\mathcal{T}_i$
,
$\mathcal{T}_i$
,
![]() $i=1,\dots, s$
, be a tree with
$i=1,\dots, s$
, be a tree with
![]() $t_i$
edges and a distinguished root, so that
$t_i$
edges and a distinguished root, so that
![]() $\mathcal{T}_i$
has
$\mathcal{T}_i$
has
![]() $t_i+1$
vertices. We construct
$t_i+1$
vertices. We construct
![]() $\Lambda =\Lambda _{\ell, t_1,\dots, t_s}$
by attaching
$\Lambda =\Lambda _{\ell, t_1,\dots, t_s}$
by attaching
![]() $\mathcal{T}_i$
to
$\mathcal{T}_i$
to
![]() $\mathcal{C}_\ell$
, using a vertex of
$\mathcal{C}_\ell$
, using a vertex of
![]() $\mathcal{C}_\ell$
as the distinguished root of
$\mathcal{C}_\ell$
as the distinguished root of
![]() $\mathcal{T}_i$
, and we may assume that
$\mathcal{T}_i$
, and we may assume that
![]() $s\leqslant \ell$
and that at most one
$s\leqslant \ell$
and that at most one
![]() $\mathcal{T}_i$
attaches to each vertex in
$\mathcal{T}_i$
attaches to each vertex in
![]() $\mathcal{C}_\ell$
. Fixing
$\mathcal{C}_\ell$
. Fixing
![]() $\Lambda$
throughout this section, we write
$\Lambda$
throughout this section, we write
![]() $\Gamma =\Gamma ^{(n,m,\ell, t)}_{\Lambda }$
as the set of all potential copies of
$\Gamma =\Gamma ^{(n,m,\ell, t)}_{\Lambda }$
as the set of all potential copies of
![]() $\Lambda$
in the uniform attachment graph
$\Lambda$
in the uniform attachment graph
![]() $G\,:\!=\,G^m_{n}$
.
$G\,:\!=\,G^m_{n}$
.
Given
![]() $\alpha \in \Gamma$
, denote by
$\alpha \in \Gamma$
, denote by
![]() $\Gamma ^-_\alpha$
the set of potential copies of
$\Gamma ^-_\alpha$
the set of potential copies of
![]() $\Lambda$
that cannot coexist with
$\Lambda$
that cannot coexist with
![]() $\alpha$
in the same instance of
$\alpha$
in the same instance of
![]() $G^m_n$
(because at least one edge is incompatible with the edges of
$G^m_n$
(because at least one edge is incompatible with the edges of
![]() $\alpha$
), and denote by
$\alpha$
), and denote by
![]() $\Gamma ^+_\alpha \subseteq \Gamma \setminus \Gamma ^-_\alpha$
the set of potential copies of
$\Gamma ^+_\alpha \subseteq \Gamma \setminus \Gamma ^-_\alpha$
the set of potential copies of
![]() $\Lambda$
that share at least one edge with
$\Lambda$
that share at least one edge with
![]() $\alpha$
, and are compatible with
$\alpha$
, and are compatible with
![]() $\alpha$
. (Note that now
$\alpha$
. (Note that now
![]() $\alpha \in \Gamma ^+_\alpha$
, unlike in Section 5.)
$\alpha \in \Gamma ^+_\alpha$
, unlike in Section 5.)
By edge independence, the covariance between
![]() $\alpha$
and any copy of
$\alpha$
and any copy of
![]() $\Lambda$
that does not belong to
$\Lambda$
that does not belong to
![]() $\Gamma ^+_\alpha \cup \Gamma ^-_\alpha$
is zero. Thus,
$\Gamma ^+_\alpha \cup \Gamma ^-_\alpha$
is zero. Thus,
Figure 4. Examples of positively correlated copies of
![]() $\Lambda$
(with
$\Lambda$
(with
![]() $\ell =3$
and
$\ell =3$
and
![]() $\mathcal{T}_1$
being a path with 2 edges). The blue dashed edges are the shared edges.
$\mathcal{T}_1$
being a path with 2 edges). The blue dashed edges are the shared edges.
Consider first the positive covariances, i.e., the first double sum in (8.3). We argue as in the estimate of (7.3). Let
![]() $\alpha \beta$
denote the union of the graphs
$\alpha \beta$
denote the union of the graphs
![]() $\alpha$
and
$\alpha$
and
![]() $\beta$
, and note that
$\beta$
, and note that
![]() ${\mathbf{1}}_\alpha{\mathbf{1}}_\beta ={\mathbf{1}}_{\alpha \beta }$
. Then
${\mathbf{1}}_\alpha{\mathbf{1}}_\beta ={\mathbf{1}}_{\alpha \beta }$
. Then
![]() $\alpha \beta$
is a connected graph, which either is unicyclic (an
$\alpha \beta$
is a connected graph, which either is unicyclic (an
![]() $\ell$
-cycle with attached trees) or multicyclic, in both cases with at most
$\ell$
-cycle with attached trees) or multicyclic, in both cases with at most
![]() $2t$
edges outside the 2-core; see Figure 4 for examples. Each graph
$2t$
edges outside the 2-core; see Figure 4 for examples. Each graph
![]() $\alpha \beta$
arises from a bounded number of pairs
$\alpha \beta$
arises from a bounded number of pairs
![]() $(\alpha, \beta )$
, and thus it follows by Theorem3.13, summing over the finitely many isomorphism types of
$(\alpha, \beta )$
, and thus it follows by Theorem3.13, summing over the finitely many isomorphism types of
![]() $\alpha \beta$
that can arise, that the expected number of pairs
$\alpha \beta$
that can arise, that the expected number of pairs
![]() $(\alpha, \beta )$
in
$(\alpha, \beta )$
in
![]() $G^m_n$
with
$G^m_n$
with
![]() $\beta \in \Gamma ^+_\alpha$
and
$\beta \in \Gamma ^+_\alpha$
and
![]() $\alpha \beta$
multicyclic is
$\alpha \beta$
multicyclic is
![]() $O(\log ^{2t}n)$
. Similarly, it follows from (3.12), again summing over a finite number of possible types of
$O(\log ^{2t}n)$
. Similarly, it follows from (3.12), again summing over a finite number of possible types of
![]() $\alpha \beta$
, that the expected number of pairs with
$\alpha \beta$
, that the expected number of pairs with
![]() $\alpha \beta$
unicyclic is
$\alpha \beta$
unicyclic is
![]() $\Theta (\log ^{2t+1}n)$
. Consequently, we have the exact order
$\Theta (\log ^{2t+1}n)$
. Consequently, we have the exact order
Furthermore, we have
![]() $0\le{\mathbb{E}}{\mathbf{1}}_\alpha{\mathbb{E}}{\mathbf{1}}_\beta \le{\mathbb{E}}{\mathbf{1}}_\alpha{\mathbf{1}}_\beta$
for all
$0\le{\mathbb{E}}{\mathbf{1}}_\alpha{\mathbb{E}}{\mathbf{1}}_\beta \le{\mathbb{E}}{\mathbf{1}}_\alpha{\mathbf{1}}_\beta$
for all
![]() $\alpha$
and
$\alpha$
and
![]() $\beta \in \Gamma ^+_\alpha$
, with
$\beta \in \Gamma ^+_\alpha$
, with
![]() ${\mathbb{E}}{\mathbf{1}}_\alpha{\mathbb{E}}{\mathbf{1}}_\beta \le \frac 12{\mathbb{E}}{\mathbf{1}}_\alpha{\mathbf{1}}_\beta$
unless both
${\mathbb{E}}{\mathbf{1}}_\alpha{\mathbb{E}}{\mathbf{1}}_\beta \le \frac 12{\mathbb{E}}{\mathbf{1}}_\alpha{\mathbf{1}}_\beta$
unless both
![]() $\alpha$
and
$\alpha$
and
![]() $\beta$
contain vertex 1, and it is easy to see that also
$\beta$
contain vertex 1, and it is easy to see that also
Alternatively, this follows from (8.4) and the argument for
![]() $\Gamma ^-_\alpha$
below.
$\Gamma ^-_\alpha$
below.
We see also that the dominant term is contributed by pairs
![]() $\alpha \in \Gamma$
and
$\alpha \in \Gamma$
and
![]() $\beta \in \Gamma ^+_\alpha$
such that
$\beta \in \Gamma ^+_\alpha$
such that
![]() $\alpha$
and
$\alpha$
and
![]() $\beta$
have the same cycle but no other common vertices.
$\beta$
have the same cycle but no other common vertices.
For the negative covariances, we show that the last double sum in (8.3) is of order
![]() $O(\log ^{2t} n )$
. To do so, we modify the argument for showing the sum in (7.4) is bounded. We construct a uniform attachment graph
$O(\log ^{2t} n )$
. To do so, we modify the argument for showing the sum in (7.4) is bounded. We construct a uniform attachment graph
![]() $G_n^{2m}$
where the first
$G_n^{2m}$
where the first
![]() $m$
out-edges of any vertex
$m$
out-edges of any vertex
![]() $2\leqslant i\leqslant n$
are coloured red, and the remaining
$2\leqslant i\leqslant n$
are coloured red, and the remaining
![]() $m$
out-edges are coloured blue. If
$m$
out-edges are coloured blue. If
![]() $\alpha$
and
$\alpha$
and
![]() $\beta$
are two potential copies of
$\beta$
are two potential copies of
![]() $\Gamma$
, let
$\Gamma$
, let
![]() $\alpha{\cdot }\beta$
be the subgraph of
$\alpha{\cdot }\beta$
be the subgraph of
![]() $K^{2m}_n$
obtained by regarding
$K^{2m}_n$
obtained by regarding
![]() $\alpha$
as living in the red part and
$\alpha$
as living in the red part and
![]() $\beta$
in the blue part, and then taking the union of them (see Figure 5 for examples). Note that if
$\beta$
in the blue part, and then taking the union of them (see Figure 5 for examples). Note that if
![]() $\beta \in \Gamma ^-_\alpha$
, then
$\beta \in \Gamma ^-_\alpha$
, then
![]() $\alpha$
and
$\alpha$
and
![]() $\beta$
must share at least one vertex. Thus,
$\beta$
must share at least one vertex. Thus,
![]() $\alpha{\cdot }\beta$
is connected; furthermore, it contains at least two cycles, and it has at most
$\alpha{\cdot }\beta$
is connected; furthermore, it contains at least two cycles, and it has at most
![]() $2t$
edges in the tree parts outside its 2-core. Once again, with some slight abuse of notation, let
$2t$
edges in the tree parts outside its 2-core. Once again, with some slight abuse of notation, let
![]() ${\mathbf{1}}_{\alpha{\cdot }\beta }$
be the indicator that
${\mathbf{1}}_{\alpha{\cdot }\beta }$
be the indicator that
![]() $\alpha{\cdot }\beta$
is present in
$\alpha{\cdot }\beta$
is present in
![]() $G^{2m}_n$
. By independence of the edges, we have
$G^{2m}_n$
. By independence of the edges, we have
![]() ${\mathbb{E}}{\mathbf{1}}_{\alpha }{\mathbb{E}}{\mathbf{1}}_{\beta }={\mathbb{E}}{\mathbf{1}}_{\alpha{\cdot }\beta }$
. Since
${\mathbb{E}}{\mathbf{1}}_{\alpha }{\mathbb{E}}{\mathbf{1}}_{\beta }={\mathbb{E}}{\mathbf{1}}_{\alpha{\cdot }\beta }$
. Since
![]() $\Lambda$
is fixed, the total negative covariance in the last sum in (8.3) can thus be bounded by some constant times the expected number of copies of subgraphs of the possible types of
$\Lambda$
is fixed, the total negative covariance in the last sum in (8.3) can thus be bounded by some constant times the expected number of copies of subgraphs of the possible types of
![]() $\alpha{\cdot }\beta$
in
$\alpha{\cdot }\beta$
in
![]() $G^{2m}_n$
. Again, Theorem3.13 implies that this is
$G^{2m}_n$
. Again, Theorem3.13 implies that this is
![]() $O(\log ^{2t}n)$
.
$O(\log ^{2t}n)$
.
Combining the estimates above of the sums in (8.3) yields the result
![]() $\sigma ^2_n=\Theta (\log ^{2t+1}n)$
.
$\sigma ^2_n=\Theta (\log ^{2t+1}n)$
.

Figure 5. Two examples of two negative correlated copies
![]() $\alpha$
and
$\alpha$
and
![]() $\beta$
that are embedded in the graph
$\beta$
that are embedded in the graph
![]() $G^{2m}_n$
, where vertex
$G^{2m}_n$
, where vertex
![]() $j$
is the common vertex and
$j$
is the common vertex and
![]() $j^{(1)}$
(left) and
$j^{(1)}$
(left) and
![]() $j^{(2)}$
(right) are the directed edges that have different recipients in
$j^{(2)}$
(right) are the directed edges that have different recipients in
![]() $\alpha$
and
$\alpha$
and
![]() $\beta$
. The red solid (resp. blue dashed) edges are the edges of
$\beta$
. The red solid (resp. blue dashed) edges are the edges of
![]() $\alpha$
(resp.
$\alpha$
(resp.
![]() $\beta$
.).
$\beta$
.).
Proof of Theorem 3.13. We have proved (3.19) in Section 8.1, and (3.20) follows from Theorem3.11 and an argument similar to the proof above of (3.13) (where we may simplify and ignore the negative terms), noting that a subgraph obtained by merging two multicyclic and leaf-free subgraphs at one or more vertices and edges is still multicyclic and leaf-free.
8.3 Proof of Theorem 3.5
We now complete the proof of Theorem 3.5 by proving the normal approximation result (3.14).
Proof of
(3.14). We bound the error terms appearing in (4.4) using the coupling described in Section 5. Let
![]() $W^s_n$
be the size-bias version of
$W^s_n$
be the size-bias version of
![]() $W_n$
defined there. For
$W_n$
defined there. For
![]() $\alpha \in \Gamma$
, let
$\alpha \in \Gamma$
, let
![]() $\Gamma ^-_\alpha$
and
$\Gamma ^-_\alpha$
and
![]() $\Gamma ^+_\alpha$
be the subsets of
$\Gamma ^+_\alpha$
be the subsets of
![]() $\Gamma$
defined at the beginning of this subsection, and let as in Section 5,
$\Gamma$
defined at the beginning of this subsection, and let as in Section 5,
![]() $G^{\alpha }$
be the graph
$G^{\alpha }$
be the graph
![]() $G$
forced to contain all edges of
$G$
forced to contain all edges of
![]() $\alpha$
. Denote by
$\alpha$
. Denote by
![]() ${\mathbf{1}}_\beta ^\alpha$
the indicator that a copy
${\mathbf{1}}_\beta ^\alpha$
the indicator that a copy
![]() $\beta$
of
$\beta$
of
![]() $\Lambda$
is in
$\Lambda$
is in
![]() $G^{\alpha }$
, and let
$G^{\alpha }$
, and let
![]() $\tilde{{\mathbf{1}}}^\alpha _\beta \,:\!=\,{\mathbf{1}}^\alpha _\beta -{\mathbf{1}}_\beta$
. Also, if
$\tilde{{\mathbf{1}}}^\alpha _\beta \,:\!=\,{\mathbf{1}}^\alpha _\beta -{\mathbf{1}}_\beta$
. Also, if
![]() $\beta \in \Gamma ^+_\alpha$
, let
$\beta \in \Gamma ^+_\alpha$
, let
![]() $\beta \setminus \alpha$
be the graph obtained from
$\beta \setminus \alpha$
be the graph obtained from
![]() $\beta$
by deleting the edges that also are in
$\beta$
by deleting the edges that also are in
![]() $\alpha$
; then
$\alpha$
; then
![]() ${\mathbf{1}}^\alpha _\beta ={\mathbf{1}}_{\beta \setminus \alpha }$
.
${\mathbf{1}}^\alpha _\beta ={\mathbf{1}}_{\beta \setminus \alpha }$
.
If
![]() $\beta \in \Gamma ^+_\alpha$
, then
$\beta \in \Gamma ^+_\alpha$
, then
![]() $\tilde{{\mathbf{1}}}^\alpha _\beta \ge 0$
since if
$\tilde{{\mathbf{1}}}^\alpha _\beta \ge 0$
since if
![]() $\beta$
exists in
$\beta$
exists in
![]() $G$
, then it will also exist in
$G$
, then it will also exist in
![]() $G^\alpha$
; furthermore, if
$G^\alpha$
; furthermore, if
![]() $\beta \in \Gamma ^-_\alpha$
, then
$\beta \in \Gamma ^-_\alpha$
, then
![]() ${\mathbf{1}}^\alpha _\beta =0$
and thus
${\mathbf{1}}^\alpha _\beta =0$
and thus
![]() $\tilde{{\mathbf{1}}}^\alpha _\beta =-{\mathbf{1}}_\beta$
, and if
$\tilde{{\mathbf{1}}}^\alpha _\beta =-{\mathbf{1}}_\beta$
, and if
![]() $\beta \notin \Gamma ^+_\alpha \cup \Gamma ^-_\alpha$
, then
$\beta \notin \Gamma ^+_\alpha \cup \Gamma ^-_\alpha$
, then
![]() $\tilde{{\mathbf{1}}}^\alpha _\beta =0$
. Hence, the construction of
$\tilde{{\mathbf{1}}}^\alpha _\beta =0$
. Hence, the construction of
![]() $W^s$
in Section 5 yields
$W^s$
in Section 5 yields
 \begin{align}{\mathbb{E}}[W^s_n-W_n\mid G]& = \sum _{\alpha \in \Gamma }\frac{{\mathbb{E}}{\mathbf{1}}_\alpha }{\mu _n}\sum _{\beta \in \Gamma }\tilde{{\mathbf{1}}}^\alpha _\beta = \sum _{\alpha \in \Gamma }\frac{{\mathbb{E}}{\mathbf{1}}_\alpha }{\mu _n} \biggl (\sum _{\beta \in \Gamma ^+_\alpha } \tilde{{\mathbf{1}}}^\alpha _{\beta } - \sum _{\beta \in \Gamma ^-_\alpha }{\mathbf{1}}_\beta \biggr ) \nonumber \\& =: \sum _{\alpha \in \Gamma }\frac{{\mathbb{E}}{\mathbf{1}}_\alpha }{\mu _n} \bigl (R^+_\alpha -R^-_\alpha \bigr ). \end{align}
\begin{align}{\mathbb{E}}[W^s_n-W_n\mid G]& = \sum _{\alpha \in \Gamma }\frac{{\mathbb{E}}{\mathbf{1}}_\alpha }{\mu _n}\sum _{\beta \in \Gamma }\tilde{{\mathbf{1}}}^\alpha _\beta = \sum _{\alpha \in \Gamma }\frac{{\mathbb{E}}{\mathbf{1}}_\alpha }{\mu _n} \biggl (\sum _{\beta \in \Gamma ^+_\alpha } \tilde{{\mathbf{1}}}^\alpha _{\beta } - \sum _{\beta \in \Gamma ^-_\alpha }{\mathbf{1}}_\beta \biggr ) \nonumber \\& =: \sum _{\alpha \in \Gamma }\frac{{\mathbb{E}}{\mathbf{1}}_\alpha }{\mu _n} \bigl (R^+_\alpha -R^-_\alpha \bigr ). \end{align}
Taking the variance yields, using the (Cauchy–Schwarz) inequality
![]() $(a+b)^2\leqslant 2(a^2+b^2)$
for all real
$(a+b)^2\leqslant 2(a^2+b^2)$
for all real
![]() $a$
and
$a$
and
![]() $b$
,
$b$
,
We proceed to bound the variances on the right-hand side. The first equals
In (8.8), we only need to consider pairs of
![]() $\gamma _1,\gamma _2$
that have at least one edge in common, since otherwise
$\gamma _1,\gamma _2$
that have at least one edge in common, since otherwise
![]() $\tilde{{\mathbf{1}}}^\alpha _{\gamma _1}$
and
$\tilde{{\mathbf{1}}}^\alpha _{\gamma _1}$
and
![]() $\tilde{{\mathbf{1}}}^\beta _{\gamma _2}$
are independent. Moreover, since
$\tilde{{\mathbf{1}}}^\beta _{\gamma _2}$
are independent. Moreover, since
![]() $\gamma _1\in \Gamma ^+_\alpha$
and
$\gamma _1\in \Gamma ^+_\alpha$
and
![]() $\gamma _2\in \Gamma ^{+}_\beta$
,
$\gamma _2\in \Gamma ^{+}_\beta$
,
![]() $\gamma _1$
has an edge (and thus a vertex) in common with
$\gamma _1$
has an edge (and thus a vertex) in common with
![]() $\alpha$
and
$\alpha$
and
![]() $\gamma _2$
has an edge (and thus a vertex) in common with
$\gamma _2$
has an edge (and thus a vertex) in common with
![]() $\beta$
. We argue similarly to the proof of (3.13) above, this time considering the uniform attachment graph
$\beta$
. We argue similarly to the proof of (3.13) above, this time considering the uniform attachment graph
![]() $G^{3m}_n$
, which we regard as three independent copies of
$G^{3m}_n$
, which we regard as three independent copies of
![]() $G$
that are coloured red, blue, and green. Let
$G$
that are coloured red, blue, and green. Let
![]() $\alpha{\cdot }\beta{*}\gamma _1\gamma _2$
be the graph formed by a red copy of
$\alpha{\cdot }\beta{*}\gamma _1\gamma _2$
be the graph formed by a red copy of
![]() $\alpha$
, a blue copy of
$\alpha$
, a blue copy of
![]() $\beta$
, and a green copy of
$\beta$
, and a green copy of
![]() $(\gamma _1\setminus \alpha )\cup (\gamma _2\setminus \beta )$
. Then
$(\gamma _1\setminus \alpha )\cup (\gamma _2\setminus \beta )$
. Then
and thus
Note that
![]() $\alpha{\cdot }\beta{*}\gamma _1\gamma _2$
is a connected graph, which has at least two cycles. The edges in the trees attached to the 2-core of
$\alpha{\cdot }\beta{*}\gamma _1\gamma _2$
is a connected graph, which has at least two cycles. The edges in the trees attached to the 2-core of
![]() $\alpha{\cdot }\beta{*}\gamma _1\gamma _2$
come from the attached trees in
$\alpha{\cdot }\beta{*}\gamma _1\gamma _2$
come from the attached trees in
![]() $\alpha, \beta, \gamma _1$
, and
$\alpha, \beta, \gamma _1$
, and
![]() $\gamma _2$
, and thus the total number of them is at most
$\gamma _2$
, and thus the total number of them is at most
![]() $4t$
. Consequently, Theorem3.13 applies. Together with (8.8)–(8.10), and summing over the finite number of possible types of the graph
$4t$
. Consequently, Theorem3.13 applies. Together with (8.8)–(8.10), and summing over the finite number of possible types of the graph
![]() $\alpha{\cdot }\beta{*}\gamma _1\gamma _2$
, we obtain
$\alpha{\cdot }\beta{*}\gamma _1\gamma _2$
, we obtain
Similarly, the second variance on the right-hand side of (8.7) equals
Again, we only need to consider pairs of
![]() $\gamma _1,\gamma _2$
that have at least one edge in common. Moreover, since
$\gamma _1,\gamma _2$
that have at least one edge in common. Moreover, since
![]() $\gamma _1\in \Gamma ^-_\alpha$
and
$\gamma _1\in \Gamma ^-_\alpha$
and
![]() $\gamma _2\in \Gamma ^{-}_\beta$
,
$\gamma _2\in \Gamma ^{-}_\beta$
,
![]() $\gamma _1$
has a vertex in common with
$\gamma _1$
has a vertex in common with
![]() $\alpha$
and
$\alpha$
and
![]() $\gamma _2$
has a vertex in common with
$\gamma _2$
has a vertex in common with
![]() $\beta$
. We consider again
$\beta$
. We consider again
![]() $G^{3m}_n$
and now let
$G^{3m}_n$
and now let
![]() $\alpha{\cdot }\beta{\cdot }\gamma _1\gamma _2$
be the graph consisting of a red copy of
$\alpha{\cdot }\beta{\cdot }\gamma _1\gamma _2$
be the graph consisting of a red copy of
![]() $\alpha$
, a blue copy of
$\alpha$
, a blue copy of
![]() $\beta$
, and green copies of
$\beta$
, and green copies of
![]() $\gamma _1$
and
$\gamma _1$
and
![]() $\gamma _2$
. Then
$\gamma _2$
. Then
and
![]() $\alpha{\cdot }\beta{\cdot }\gamma _1\gamma _2$
is a connected graph with at least three cycles and at most
$\alpha{\cdot }\beta{\cdot }\gamma _1\gamma _2$
is a connected graph with at least three cycles and at most
![]() $4t$
edges outside its 2-core. Consequently, we now obtain from (3.12) and Theorem3.13
$4t$
edges outside its 2-core. Consequently, we now obtain from (3.12) and Theorem3.13
By (8.7) and the bounds (8.11) and (8.14) above, we deduce that
Moreover,
![]() $W_n$
is determined by
$W_n$
is determined by
![]() $G$
, and thus the conditional Jensen’s inequality yields
$G$
, and thus the conditional Jensen’s inequality yields
Noting also that
![]() $\sigma ^2_n=\Theta (\log ^{2t+1}n)$
by (3.13), the first error term in (4.4) is therefore
$\sigma ^2_n=\Theta (\log ^{2t+1}n)$
by (3.13), the first error term in (4.4) is therefore
We now turn to the second error term in (4.4). By first conditioning on the graph
![]() $G$
, we have in analogy with (8.6),
$G$
, we have in analogy with (8.6),
and thus
We argue as above. The first sum on the right-hand side equals
Hence, using (8.9),
where
![]() $\alpha{*}\gamma _1\gamma _2$
is the subgraph formed by a red copy of
$\alpha{*}\gamma _1\gamma _2$
is the subgraph formed by a red copy of
![]() $\alpha$
and a blue copy of
$\alpha$
and a blue copy of
![]() $(\gamma _1\setminus \alpha )\cup (\gamma _2\setminus \alpha )$
, regarded as a subgraph of
$(\gamma _1\setminus \alpha )\cup (\gamma _2\setminus \alpha )$
, regarded as a subgraph of
![]() $K^{2m}_n$
coloured red and blue as above, and
$K^{2m}_n$
coloured red and blue as above, and
![]() ${\mathbf{1}}_{\alpha{*}\gamma _1\gamma _2}$
is the indicator that this subgraph exists in
${\mathbf{1}}_{\alpha{*}\gamma _1\gamma _2}$
is the indicator that this subgraph exists in
![]() $G^{2m}_n$
. Since
$G^{2m}_n$
. Since
![]() $\gamma _1,\gamma _2\in \Gamma _\alpha ^+$
, they have at least one vertex each in common with
$\gamma _1,\gamma _2\in \Gamma _\alpha ^+$
, they have at least one vertex each in common with
![]() $\alpha$
, and thus
$\alpha$
, and thus
![]() $\alpha{*}\gamma _1\gamma _2$
is connected. Moreover,
$\alpha{*}\gamma _1\gamma _2$
is connected. Moreover,
![]() $\alpha{*}\gamma _1\gamma _2$
has at least one cycle, and at most
$\alpha{*}\gamma _1\gamma _2$
has at least one cycle, and at most
![]() $3t$
edges outside its 2-core. Consequently, we now obtain from (3.12) and Theorem3.13
$3t$
edges outside its 2-core. Consequently, we now obtain from (3.12) and Theorem3.13
Similarly, the second sum in (8.19) equals
 \begin{align} B_2&\,:\!=\,\sum _{\alpha \in \Gamma }{\mathbb{E}}{\mathbf{1}}_\alpha \sum _{\gamma _1\in \Gamma ^-_\alpha }\sum _{\gamma _2\in \Gamma ^{-}_\alpha } \operatorname{Cov}\bigl ({\mathbf{1}}_{\gamma _1},{\mathbf{1}}_{\gamma _2}\bigr ) \leqslant \sum _{\alpha \in \Gamma } \sum _{\gamma _1\in \Gamma ^-_\alpha }\sum _{\gamma _2\in \Gamma ^{-}_\alpha }{\mathbb{E}}{\mathbf{1}}_\alpha{\mathbb{E}}\bigl [{\mathbf{1}}_{\gamma _1}{\mathbf{1}}_{\gamma _2}\bigr ] \notag \\&\phantom : = \sum _{\alpha \in \Gamma } \sum _{\gamma _1\in \Gamma ^-_\alpha }\sum _{\gamma _2\in \Gamma ^{-}_\alpha }{\mathbb{E}}{\mathbf{1}}_{\alpha{\cdot }\gamma _1\gamma _2}, \end{align}
\begin{align} B_2&\,:\!=\,\sum _{\alpha \in \Gamma }{\mathbb{E}}{\mathbf{1}}_\alpha \sum _{\gamma _1\in \Gamma ^-_\alpha }\sum _{\gamma _2\in \Gamma ^{-}_\alpha } \operatorname{Cov}\bigl ({\mathbf{1}}_{\gamma _1},{\mathbf{1}}_{\gamma _2}\bigr ) \leqslant \sum _{\alpha \in \Gamma } \sum _{\gamma _1\in \Gamma ^-_\alpha }\sum _{\gamma _2\in \Gamma ^{-}_\alpha }{\mathbb{E}}{\mathbf{1}}_\alpha{\mathbb{E}}\bigl [{\mathbf{1}}_{\gamma _1}{\mathbf{1}}_{\gamma _2}\bigr ] \notag \\&\phantom : = \sum _{\alpha \in \Gamma } \sum _{\gamma _1\in \Gamma ^-_\alpha }\sum _{\gamma _2\in \Gamma ^{-}_\alpha }{\mathbb{E}}{\mathbf{1}}_{\alpha{\cdot }\gamma _1\gamma _2}, \end{align}
where
![]() $\alpha{\cdot }\gamma _1\gamma _2$
is the subgraph formed by a red copy of
$\alpha{\cdot }\gamma _1\gamma _2$
is the subgraph formed by a red copy of
![]() $\alpha$
and a blue copy of
$\alpha$
and a blue copy of
![]() $\gamma _1\cup \gamma _2$
. We obtain from (3.12) and Theorem3.13
$\gamma _1\cup \gamma _2$
. We obtain from (3.12) and Theorem3.13
We obtain from (8.19), (8.22), and (8.24) that
By this and (3.13), we conclude that the second error term in (4.4) is
Finally, we use (8.17) and (8.26) in (4.4) and obtain (3.14), which completes the proof of Theorem 3.5.
9. Proof of the normal approximations for trees
In this section we prove Theorem 3.7 and Theorem3.9.
9.1 Proof of Theorem 3.7
We start by proving (3.16): By Lemma 6.4 (i) and (6.1), an upper bound is, by summing in the order
![]() $k_1,\dots, k_t$
,
$k_1,\dots, k_t$
,
 \begin{align} \mu _n \leqslant C \sum _{1\leqslant k_1\lt \dots \lt k_t\leqslant n}\prod ^t_{i=2}\frac{1}{k_i-1} \leqslant C \sum _{k_t\leqslant n}1= Cn, \end{align}
\begin{align} \mu _n \leqslant C \sum _{1\leqslant k_1\lt \dots \lt k_t\leqslant n}\prod ^t_{i=2}\frac{1}{k_i-1} \leqslant C \sum _{k_t\leqslant n}1= Cn, \end{align}
The lower bound follows similarly, or simply because there are
![]() $\Theta (n^t)$
potential copies of
$\Theta (n^t)$
potential copies of
![]() $\Lambda$
, and each has probability
$\Lambda$
, and each has probability
![]() $\geqslant n^{-(t-1)}$
.
$\geqslant n^{-(t-1)}$
.
(3.17): To obtain an upper bound on
![]() $\sigma ^2_n$
, we argue as in the proof of (3.13). We use again (8.3), and the only difference from the argument in Section 8 is that for
$\sigma ^2_n$
, we argue as in the proof of (3.13). We use again (8.3), and the only difference from the argument in Section 8 is that for
![]() $\alpha \in \Gamma$
and
$\alpha \in \Gamma$
and
![]() $\beta \in \Gamma ^{+}_\alpha$
, their union
$\beta \in \Gamma ^{+}_\alpha$
, their union
![]() $\alpha \beta$
does not have to contain a cycle; however, it is always a connected graph with at most
$\alpha \beta$
does not have to contain a cycle; however, it is always a connected graph with at most
![]() $2t$
edges. There is still a finite number of types of
$2t$
edges. There is still a finite number of types of
![]() $\alpha \beta$
, and we obtain by using (depending on the number of cycles in
$\alpha \beta$
, and we obtain by using (depending on the number of cycles in
![]() $\alpha \beta$
) (3.16), (3.12) and Theorem3.13
$\alpha \beta$
) (3.16), (3.12) and Theorem3.13
which implies (3.17).
If
![]() $\sigma ^2_n=\Theta (n)$
, then we can use Theorem4.3 to prove the asymptotic normality of
$\sigma ^2_n=\Theta (n)$
, then we can use Theorem4.3 to prove the asymptotic normality of
![]() $W_n$
in a similar vein as before. Again, we argue as in the proof of Theorem 3.5 in Section 8, and the only difference is that the graphs
$W_n$
in a similar vein as before. Again, we argue as in the proof of Theorem 3.5 in Section 8, and the only difference is that the graphs
![]() $\alpha{\cdot }\beta{*}\gamma _1\gamma _2$
,
$\alpha{\cdot }\beta{*}\gamma _1\gamma _2$
,
![]() $\alpha{\cdot }\beta{\cdot }\gamma _1\gamma _2$
,
$\alpha{\cdot }\beta{\cdot }\gamma _1\gamma _2$
,
![]() $\alpha{*}\gamma _1\gamma _2$
,
$\alpha{*}\gamma _1\gamma _2$
,
![]() $\alpha{\cdot }\gamma _1\gamma _2$
do not have to contain a cycle. As in the estimation of variance above, we therefore use not only (3.12) and Theorem3.13 but also (3.16) in the estimates; as a result we obtain the bound
$\alpha{\cdot }\gamma _1\gamma _2$
do not have to contain a cycle. As in the estimation of variance above, we therefore use not only (3.12) and Theorem3.13 but also (3.16) in the estimates; as a result we obtain the bound
![]() $O(n)$
in (8.15) and (8.25). Hence, if
$O(n)$
in (8.15) and (8.25). Hence, if
![]() $\sigma _n^2=\Theta (n)$
, the terms in (4.4) are
$\sigma _n^2=\Theta (n)$
, the terms in (4.4) are
implying (3.18).
9.2 Proof of Theorem3.9.
Recall that the upper bound
![]() $O(n)$
for the variance
$O(n)$
for the variance
![]() $\sigma ^2_n$
is already proved in (3.17). To obtain a lower bound, we state and prove the following general lemma. In our application of it,
$\sigma ^2_n$
is already proved in (3.17). To obtain a lower bound, we state and prove the following general lemma. In our application of it,
![]() $X$
and
$X$
and
![]() $\xi _\nu$
will be taken as the count of trees
$\xi _\nu$
will be taken as the count of trees
![]() $W_n$
and the recipient of a directed edge
$W_n$
and the recipient of a directed edge
![]() $\nu$
in the uniform attachment graph
$\nu$
in the uniform attachment graph
![]() $G^m_n$
.
$G^m_n$
.
Lemma 9.1.
Let
![]() $(\xi _\nu )_{\nu \in \mathcal I}$
be a family of independent random variables (where
$(\xi _\nu )_{\nu \in \mathcal I}$
be a family of independent random variables (where
![]() $\mathcal I$
is an arbitrary index set), and let
$\mathcal I$
is an arbitrary index set), and let
![]() $X$
be any random variable such that
$X$
be any random variable such that
![]() ${\mathbb{E}} X^2\lt \infty$
. For each
${\mathbb{E}} X^2\lt \infty$
. For each
![]() $\nu \in \mathcal I$
, let
$\nu \in \mathcal I$
, let
Then
Proof. Assume first that
![]() $\mathcal I$
is finite and define
$\mathcal I$
is finite and define
Note that
It follows from (9.4) that the random variable
![]() $X_\nu$
is a function of
$X_\nu$
is a function of
![]() $\xi _\nu$
. Consequently, the variables
$\xi _\nu$
. Consequently, the variables
![]() $X_\nu$
are independent, and thus
$X_\nu$
are independent, and thus
Moreover, (9.4) implies also
Consequently,
Hence,
and thus
 \begin{align} {\mathbb{E}}\left [{(X-{\mathbb{E}} X)^2}\right ]& ={\mathbb{E}}\left [{(X-{\mathbb{E}} X-Y)^2}\right ] +2{\mathbb{E}}\left [{(X-{\mathbb{E}} X-Y)Y}\right ] +{\mathbb{E}}\left [{Y^2}\right ] \notag \\& ={\mathbb{E}}\left [{(X-{\mathbb{E}} X-Y)^2}\right ] +{\mathbb{E}}\left [{Y^2}\right ] \notag \\& \geq{\mathbb{E}}\left [{Y^2}\right ]. \end{align}
\begin{align} {\mathbb{E}}\left [{(X-{\mathbb{E}} X)^2}\right ]& ={\mathbb{E}}\left [{(X-{\mathbb{E}} X-Y)^2}\right ] +2{\mathbb{E}}\left [{(X-{\mathbb{E}} X-Y)Y}\right ] +{\mathbb{E}}\left [{Y^2}\right ] \notag \\& ={\mathbb{E}}\left [{(X-{\mathbb{E}} X-Y)^2}\right ] +{\mathbb{E}}\left [{Y^2}\right ] \notag \\& \geq{\mathbb{E}}\left [{Y^2}\right ]. \end{align}
The result follows from (9.12) and (9.8), which completes the proof for finite
![]() $\mathcal I$
.
$\mathcal I$
.
If
![]() $\mathcal I$
is infinite, the case just proved shows that for every finite subset
$\mathcal I$
is infinite, the case just proved shows that for every finite subset
![]() $\mathcal I_1\subset \mathcal I$
, we have
$\mathcal I_1\subset \mathcal I$
, we have
which implies (9.5).
Remark 9.2. From a more abstract point of view, a minor modification of the proof above shows that
![]() $Y$
is the orthogonal projection of
$Y$
is the orthogonal projection of
![]() $X-{\mathbb{E}} X$
onto the linear subspace of
$X-{\mathbb{E}} X$
onto the linear subspace of
![]() $L^2$
consisting of sums of the type
$L^2$
consisting of sums of the type
![]() $\sum _{\nu \in \mathcal I} f_\nu (\xi _\nu )$
, and the inequality (9.5) is thus an instance of the fact that orthogonal projections in
$\sum _{\nu \in \mathcal I} f_\nu (\xi _\nu )$
, and the inequality (9.5) is thus an instance of the fact that orthogonal projections in
![]() $L^2$
never increase the variance (or the norm).
$L^2$
never increase the variance (or the norm).
Proof of Theorem
3.9. Fix
![]() $j\in [n]$
and
$j\in [n]$
and
![]() $a\in [m]$
. Recall that the edge
$a\in [m]$
. Recall that the edge
![]() $j^{(a)}$
in
$j^{(a)}$
in
![]() $G^m_n$
is randomly chosen as one of the edges
$G^m_n$
is randomly chosen as one of the edges
![]() $ji^{(a)}$
(
$ji^{(a)}$
(
![]() $i\in [j-1]$
) in
$i\in [j-1]$
) in
![]() $K^m_n$
; we denote the recipient of the edge
$K^m_n$
; we denote the recipient of the edge
![]() $j^{(a)}$
by
$j^{(a)}$
by
![]() $\xi =\xi _{j,a}$
; thus
$\xi =\xi _{j,a}$
; thus
![]() $\xi$
is uniformly distributed on
$\xi$
is uniformly distributed on
![]() $[j-1]$
, and
$[j-1]$
, and
![]() $j^{(a)}=j\xi ^{(a)}$
. We condition on
$j^{(a)}=j\xi ^{(a)}$
. We condition on
![]() $\xi$
, and decompose
$\xi$
, and decompose
![]() $W_n$
as
$W_n$
as
where
-
•
 $W_n^{(0)}$
is the number of copies of
$W_n^{(0)}$
is the number of copies of
 $S_\ell$
that do not contain the edge
$S_\ell$
that do not contain the edge
 $ji^{(a)}$
for any
$ji^{(a)}$
for any
 $i\in [j-1]$
.
$i\in [j-1]$
. -
•
 $W_n^{(1)}$
is the number of copies
$W_n^{(1)}$
is the number of copies
 $\alpha$
of
$\alpha$
of
 $S_\ell$
that contain
$S_\ell$
that contain
 $j^{(a)}=j\xi ^{(a)}$
and such that the center of
$j^{(a)}=j\xi ^{(a)}$
and such that the center of
 $\alpha$
is
$\alpha$
is
 $j$
.
$j$
. -
•
 $W_n^{(2)}$
is the number of copies
$W_n^{(2)}$
is the number of copies
 $\alpha$
of
$\alpha$
of
 $S_\ell$
that contain
$S_\ell$
that contain
 $j^{(a)}=j\xi ^{(a)}$
and such that the center of
$j^{(a)}=j\xi ^{(a)}$
and such that the center of
 $\alpha$
is
$\alpha$
is
 $\xi$
.
$\xi$
.
Then
![]() $W_n^{(0)}$
is clearly independent of
$W_n^{(0)}$
is clearly independent of
![]() $\xi$
. Moreover, for every
$\xi$
. Moreover, for every
![]() $i\lt j$
,
$i\lt j$
,
![]() ${\mathbb{E}}(W_n^{(1)}\mid \xi =i)$
is the expected number of stars
${\mathbb{E}}(W_n^{(1)}\mid \xi =i)$
is the expected number of stars
![]() $S_{\ell -1}$
with center
$S_{\ell -1}$
with center
![]() $j$
and
$j$
and
![]() $\ell -1$
leaves in
$\ell -1$
leaves in
![]() $[n]\setminus{\{i,j\}}$
. Since the edges from
$[n]\setminus{\{i,j\}}$
. Since the edges from
![]() $j$
have their endpoints uniformly distributed in
$j$
have their endpoints uniformly distributed in
![]() $[j-1]$
, this number does not depend on
$[j-1]$
, this number does not depend on
![]() $i$
. In other words,
$i$
. In other words,
![]() ${\mathbb{E}}(W_n^{(1)}\mid \xi )$
does not depend on
${\mathbb{E}}(W_n^{(1)}\mid \xi )$
does not depend on
![]() $\xi$
.
$\xi$
.
Similarly,
![]() ${\mathbb{E}}(W_n^{(2)}\mid \xi =i)$
is the expected number of stars
${\mathbb{E}}(W_n^{(2)}\mid \xi =i)$
is the expected number of stars
![]() $S_{\ell -1}$
with center
$S_{\ell -1}$
with center
![]() $i$
and
$i$
and
![]() $\ell -1$
leaves in
$\ell -1$
leaves in
![]() $[n]\setminus{\{i,j\}}$
. Hence,
$[n]\setminus{\{i,j\}}$
. Hence,
 \begin{align}{\mathbb{E}}\bigl (W_n^{(2)}\mid \xi =i\bigr )=\sum _{q=0}^{\ell -1}W^{\prime}_{j,i,q}, \end{align}
\begin{align}{\mathbb{E}}\bigl (W_n^{(2)}\mid \xi =i\bigr )=\sum _{q=0}^{\ell -1}W^{\prime}_{j,i,q}, \end{align}
where
![]() $W^{\prime}_{j,i,q}$
is the number of such copies of
$W^{\prime}_{j,i,q}$
is the number of such copies of
![]() $S_{\ell -1}$
with
$S_{\ell -1}$
with
![]() $q$
leaves in
$q$
leaves in
![]() $(i,n]$
and
$(i,n]$
and
![]() $r\,:\!=\,\ell -1-q$
in
$r\,:\!=\,\ell -1-q$
in
![]() $[1,i)$
. Assume for simplicity that
$[1,i)$
. Assume for simplicity that
![]() $i\geqslant n/10$
. Then, counting the number of ways to choose first the vertices and then the edges of such a copy, and multiplying with the probability that it exists in
$i\geqslant n/10$
. Then, counting the number of ways to choose first the vertices and then the edges of such a copy, and multiplying with the probability that it exists in
![]() $G^m_n$
,
$G^m_n$
,
 \begin{align}{\mathbb{E}}W^{\prime}_{j,i,q} & = \binom{i-1}r\sum _{\substack{i\lt i_1\lt \dots \lt i_q\leqslant n\\i_1,\dots, i_q\neq j}} \binom{m}{r} r!\, m^q(i-1)^{-r}\prod _{k=1}^q(i_k-1)^{-1} \notag \\& =\Bigl (1+O\Bigl (\frac{1}n\Bigr )\Bigr ) \binom{m}{r} m^q\frac{1}{q!} \left (\sum _{p=i+1}^n\frac{1}{p-1}+O\Bigl (\frac{1}{n}\Bigr )\right )^q \notag \\& = \binom{m}{r} \frac{m^q}{q!} \log ^q \Bigl (\frac{n}{i}\Bigr ) +O\Bigl (\frac{1}n\Bigr ) . \end{align}
\begin{align}{\mathbb{E}}W^{\prime}_{j,i,q} & = \binom{i-1}r\sum _{\substack{i\lt i_1\lt \dots \lt i_q\leqslant n\\i_1,\dots, i_q\neq j}} \binom{m}{r} r!\, m^q(i-1)^{-r}\prod _{k=1}^q(i_k-1)^{-1} \notag \\& =\Bigl (1+O\Bigl (\frac{1}n\Bigr )\Bigr ) \binom{m}{r} m^q\frac{1}{q!} \left (\sum _{p=i+1}^n\frac{1}{p-1}+O\Bigl (\frac{1}{n}\Bigr )\right )^q \notag \\& = \binom{m}{r} \frac{m^q}{q!} \log ^q \Bigl (\frac{n}{i}\Bigr ) +O\Bigl (\frac{1}n\Bigr ) . \end{align}
Since
![]() $\log (n/i)$
is positive and monotonically decreasing in
$\log (n/i)$
is positive and monotonically decreasing in
![]() $i\in [n/10,n)$
, it follows that if
$i\in [n/10,n)$
, it follows that if
![]() $\frac{n}{10}\leqslant i\leqslant k\lt j\leqslant n$
, then
$\frac{n}{10}\leqslant i\leqslant k\lt j\leqslant n$
, then
 \begin{align}{\mathbb{E}}\bigl (W_n\mid \xi =i\bigr ) -{\mathbb{E}}\bigl (W_n\mid \xi =k\bigr )& ={\mathbb{E}}\bigl (W_n^{(2)}\mid \xi =i\bigr ) -{\mathbb{E}}\bigl (W_n^{(2)}\mid \xi =k\bigr ) \notag \\& =\sum _{q=0}^{\ell -1}\bigl (W^{\prime}_{j,i,q}-W^{\prime}_{j,k,q}\bigr ) \notag \\& =\sum _{q=0}^{\ell -1}\binom{m}{r}\frac{m^q}{q!} \Bigl (\log ^q \Bigl (\frac{n}{i}\Bigr )-\log ^q \Bigl (\frac{n}{k}\Bigr ) +O\Bigl (\frac{1}n\Bigr )\Bigr ) \notag \\& \geqslant \frac{m^{\ell -1}}{(\ell -1)!} \Bigl (\log ^{\ell -1} \Bigl (\frac{n}{i}\Bigr )-\log ^{\ell -1}\Bigl ( \frac{n}{k}\Bigr )\Bigr ) +O\Bigl (\frac{1}n\Bigr ) . \end{align}
\begin{align}{\mathbb{E}}\bigl (W_n\mid \xi =i\bigr ) -{\mathbb{E}}\bigl (W_n\mid \xi =k\bigr )& ={\mathbb{E}}\bigl (W_n^{(2)}\mid \xi =i\bigr ) -{\mathbb{E}}\bigl (W_n^{(2)}\mid \xi =k\bigr ) \notag \\& =\sum _{q=0}^{\ell -1}\bigl (W^{\prime}_{j,i,q}-W^{\prime}_{j,k,q}\bigr ) \notag \\& =\sum _{q=0}^{\ell -1}\binom{m}{r}\frac{m^q}{q!} \Bigl (\log ^q \Bigl (\frac{n}{i}\Bigr )-\log ^q \Bigl (\frac{n}{k}\Bigr ) +O\Bigl (\frac{1}n\Bigr )\Bigr ) \notag \\& \geqslant \frac{m^{\ell -1}}{(\ell -1)!} \Bigl (\log ^{\ell -1} \Bigl (\frac{n}{i}\Bigr )-\log ^{\ell -1}\Bigl ( \frac{n}{k}\Bigr )\Bigr ) +O\Bigl (\frac{1}n\Bigr ) . \end{align}
In particular, if
![]() $i\in [n/10,n/4]$
and
$i\in [n/10,n/4]$
and
![]() $k\in [n/3,n/2]$
, then
$k\in [n/3,n/2]$
, then
for some
![]() $c\gt 0$
if
$c\gt 0$
if
![]() $n$
is large enough, say
$n$
is large enough, say
![]() $n\geqslant n_1$
.
$n\geqslant n_1$
.
Let
![]() $\xi ^{\prime}$
be an independent copy of
$\xi ^{\prime}$
be an independent copy of
![]() $\xi =\xi _{j,a}$
and write
$\xi =\xi _{j,a}$
and write
![]() $g(\xi )\,:\!=\,{\mathbb{E}}(W_n\mid \xi )$
. Assume
$g(\xi )\,:\!=\,{\mathbb{E}}(W_n\mid \xi )$
. Assume
![]() $n\geqslant n_1$
. Then (9.18) shows that
$n\geqslant n_1$
. Then (9.18) shows that
![]() $g(i)-g(k)\geqslant c$
if
$g(i)-g(k)\geqslant c$
if
![]() $i\in [n/10,n/4]$
and
$i\in [n/10,n/4]$
and
![]() $k\in [n/3,n/2]$
; hence it follows that if
$k\in [n/3,n/2]$
; hence it follows that if
![]() $j\gt n/2$
, then
$j\gt n/2$
, then
 \begin{align} \operatorname{Var}\bigl [{\mathbb{E}}(W_n\mid \xi )\bigr ] &=\operatorname{Var} g(\xi ) =\tfrac 12{\mathbb{E}}\left (g(\xi )-g(\xi ^{\prime})\right )^2 \notag \\& \geqslant \tfrac 12\mathbb{P}\bigl (\xi \in [n/10,n/4]\bigr )\mathbb{P}\bigl (\xi ^{\prime}\in [n/3,n/2]\bigr ) c^2 \geqslant c_1, \end{align}
\begin{align} \operatorname{Var}\bigl [{\mathbb{E}}(W_n\mid \xi )\bigr ] &=\operatorname{Var} g(\xi ) =\tfrac 12{\mathbb{E}}\left (g(\xi )-g(\xi ^{\prime})\right )^2 \notag \\& \geqslant \tfrac 12\mathbb{P}\bigl (\xi \in [n/10,n/4]\bigr )\mathbb{P}\bigl (\xi ^{\prime}\in [n/3,n/2]\bigr ) c^2 \geqslant c_1, \end{align}
for some constant
![]() $c_1\gt 0$
.
$c_1\gt 0$
.
We now apply Lemma 9.1 with the family of all random variables
![]() $\xi _{j,a}$
, thus letting
$\xi _{j,a}$
, thus letting
![]() $\mathcal I={\{2,\dots, n\}}\times [m]$
. Then (9.5) and the lower bound in (9.19) (for
$\mathcal I={\{2,\dots, n\}}\times [m]$
. Then (9.5) and the lower bound in (9.19) (for
![]() $j\geqslant n/2$
) show that for
$j\geqslant n/2$
) show that for
![]() $n\geqslant n_1$
,
$n\geqslant n_1$
,
 \begin{align}{\mathrm{Var}}(W_n) \geqslant \sum ^n_{j=\lceil{n/2}\rceil } \sum ^m_{a=1} c_1 = \Omega (n). \end{align}
\begin{align}{\mathrm{Var}}(W_n) \geqslant \sum ^n_{j=\lceil{n/2}\rceil } \sum ^m_{a=1} c_1 = \Omega (n). \end{align}
Since
![]() $\operatorname{Var} W_n = \sigma _n^2=O(n)$
by (3.17), this completes the proof.
$\operatorname{Var} W_n = \sigma _n^2=O(n)$
by (3.17), this completes the proof.
10. Proof of Theorem 3.15
Proof of Theorem
3.15. Let
![]() $h^{\prime}$
be the number of vertices in
$h^{\prime}$
be the number of vertices in
![]() $H^{\prime}$
, and let
$H^{\prime}$
, and let
![]() $r\in [h]$
be the number of them such that attaching an edge at that vertex yields a copy of
$r\in [h]$
be the number of them such that attaching an edge at that vertex yields a copy of
![]() $H$
.
$H$
.
Fix a copy
![]() $H^{\prime}_0$
of
$H^{\prime}_0$
of
![]() $H^{\prime}$
in
$H^{\prime}$
in
![]() $G^m_\infty$
, and let its vertices be
$G^m_\infty$
, and let its vertices be
![]() $k_1\lt \cdots \lt k_{h^{\prime}}$
. For every
$k_1\lt \cdots \lt k_{h^{\prime}}$
. For every
![]() $j\in \mathbb N$
and
$j\in \mathbb N$
and
![]() $a\in [m]$
, let
$a\in [m]$
, let
![]() $I_{ja}$
be the indicator of the event that the edge
$I_{ja}$
be the indicator of the event that the edge
![]() $j^{(a)}$
in
$j^{(a)}$
in
![]() $G^n_m$
has exactly one endpoint in
$G^n_m$
has exactly one endpoint in
![]() $H^{\prime}_0$
and moreover that attaching
$H^{\prime}_0$
and moreover that attaching
![]() $j^{(a)}$
to
$j^{(a)}$
to
![]() $H^{\prime}_0$
yields a copy of
$H^{\prime}_0$
yields a copy of
![]() $H$
. Then, for
$H$
. Then, for
![]() $n\geqslant k_{h^{\prime}}$
, the number of copies of
$n\geqslant k_{h^{\prime}}$
, the number of copies of
![]() $H$
in
$H$
in
![]() $G^m_n$
that contain the given subgraph
$G^m_n$
that contain the given subgraph
![]() $H^{\prime}_0$
is
$H^{\prime}_0$
is
 \begin{align} W_n^{H^{\prime}_0}\,:\!=\,\sum _{j=1}^n\sum _{a=1}^m I_{ja} = \sum _{j = k_{h^{\prime}}+1}^n\sum _{a=1}^m I_{ja} +O(1). \end{align}
\begin{align} W_n^{H^{\prime}_0}\,:\!=\,\sum _{j=1}^n\sum _{a=1}^m I_{ja} = \sum _{j = k_{h^{\prime}}+1}^n\sum _{a=1}^m I_{ja} +O(1). \end{align}
Condition on the existence of
![]() $H_0^{\prime}$
. Then the variables
$H_0^{\prime}$
. Then the variables
![]() $I_{ja}$
in the final sum are independent and have the Bernoulli distributions
$I_{ja}$
in the final sum are independent and have the Bernoulli distributions
![]() $\operatorname{Be}(r/(j-1))$
. It follows by the lemma below that as
$\operatorname{Be}(r/(j-1))$
. It follows by the lemma below that as
![]() ${n\to \infty }$
,
${n\to \infty }$
,
![]() $W_n^{H^{\prime}_0}/\log n \overset{\mathrm{a.s.}}{\longrightarrow } rm$
. Thus, every copy of
$W_n^{H^{\prime}_0}/\log n \overset{\mathrm{a.s.}}{\longrightarrow } rm$
. Thus, every copy of
![]() $H^{\prime}$
in
$H^{\prime}$
in
![]() $G^m_\infty$
has asymptotically
$G^m_\infty$
has asymptotically
![]() $rm\log n$
attached edges that make copies of
$rm\log n$
attached edges that make copies of
![]() $H$
. Summing over the a.s. finite number of copies
$H$
. Summing over the a.s. finite number of copies
![]() $H^{\prime}_0$
of
$H^{\prime}_0$
of
![]() $H^{\prime}$
in
$H^{\prime}$
in
![]() $G^m_\infty$
, we obtain
$G^m_\infty$
, we obtain
which verifies Conjecture 3.14 in this case.
The proof used the following simple law of large numbers; it is certainly known but for completeness we include a proof.
Lemma 10.1.
Let
![]() $I_i\in \operatorname{Be}(p_i)$
be independent random variables with
$I_i\in \operatorname{Be}(p_i)$
be independent random variables with
![]() $p_i\in [0,1]$
, for
$p_i\in [0,1]$
, for
![]() $i=1,2,\dots$
. If
$i=1,2,\dots$
. If
![]() $\sum _{i=1}^\infty p_i=\infty$
, then
$\sum _{i=1}^\infty p_i=\infty$
, then
Proof. Let
![]() $b_n\,:\!=\,\sum _{i=1}^n p_i$
. We have
$b_n\,:\!=\,\sum _{i=1}^n p_i$
. We have
 \begin{align} \sum _{n=1}^\infty \frac{{\mathbb{E}}(I_n-p_n)^2}{b^2_n}& \leqslant \sum _{n=1}^\infty \frac{p_n}{b_n^2} =\frac{1}{p_1}+\sum _{n=2}^\infty \frac{b_n-b_{n-1}}{b_n^2} \leqslant \frac{1}{p_1}+\sum _{n=2}^\infty \int _{b_{n-1}}^{b_n}\frac{\mathrm{d} s}{s^2} \notag \\& =\frac{1}{p_1}+ \int _{b_{1}}^\infty \frac{\mathrm{d} s}{s^2} \lt \infty . \end{align}
\begin{align} \sum _{n=1}^\infty \frac{{\mathbb{E}}(I_n-p_n)^2}{b^2_n}& \leqslant \sum _{n=1}^\infty \frac{p_n}{b_n^2} =\frac{1}{p_1}+\sum _{n=2}^\infty \frac{b_n-b_{n-1}}{b_n^2} \leqslant \frac{1}{p_1}+\sum _{n=2}^\infty \int _{b_{n-1}}^{b_n}\frac{\mathrm{d} s}{s^2} \notag \\& =\frac{1}{p_1}+ \int _{b_{1}}^\infty \frac{\mathrm{d} s}{s^2} \lt \infty . \end{align}
Since the
![]() $I_n$
are independent, it follows that
$I_n$
are independent, it follows that
![]() $b_n^{-1}\sum _{i=1}^n (I_i-p_i)\overset{\mathrm{a.s.}}{\longrightarrow }0$
, see [ [Reference Feller8], Theorem VII.8.3], which is equivalent to (10.3).
$b_n^{-1}\sum _{i=1}^n (I_i-p_i)\overset{\mathrm{a.s.}}{\longrightarrow }0$
, see [ [Reference Feller8], Theorem VII.8.3], which is equivalent to (10.3).
Acknowledgement
We thank Nathan Ross for pointing us to some results in Stein’s method, and Tiffany Y. Y. Lo also would like to express her gratitude to Nathan Ross for his encouragement at the earlier stage of this project.