In this work the $\ell_q$ -norms of points chosen uniformly at random in a centered regular simplex in high dimensions are studied. Berry–Esseen bounds in the regime $1\leq q < \infty$ are derived and complemented by a non-central limit theorem together with moderate and large deviations in the case where $q=\infty$ . An application to the intersection volume of a regular simplex with an $\ell_p^n$ -ball is also carried out.

We consider the numerical approximation of the filtering problem in high dimensions, that is, when the hidden state lies in ℝd with large d. For low-dimensional problems, one of the most popular numerical procedures for consistent inference is the class of approximations termed particle filters or sequential Monte Carlo methods. However, in high dimensions, standard particle filters (e.g. the bootstrap particle filter) can have a cost that is exponential in d for the algorithm to be stable in an appropriate sense. We develop a new particle filter, called the space‒time particle filter, for a specific family of state-space models in discrete time. This new class of particle filters provides consistent Monte Carlo estimates for any fixed d, as do standard particle filters. Moreover, when there is a spatial mixing element in the dimension of the state vector, the space‒time particle filter will scale much better with d than the standard filter for a class of filtering problems. We illustrate this analytically for a model of a simple independent and identically distributed structure and a model of an L-Markovian structure (L≥ 1, L independent of d) in the d-dimensional space direction, when we show that the algorithm exhibits certain stability properties as d increases at a cost 𝒪(nNd2), where n is the time parameter and N is the number of Monte Carlo samples, which are fixed and independent of d. Our theoretical results are also supported by numerical simulations on practical models of complex structures. The results suggest that it is indeed possible to tackle some high-dimensional filtering problems using the space‒time particle filter that standard particle filters cannot handle.

We study a parametric class of isotropic but not necessarily stationary Poisson hyperplane tessellations in n-dimensional Euclidean space. Our focus is on the volume of the zero cell, i.e. the cell containing the origin. As a main result, we obtain an explicit formula for the variance of the volume of the zero cell in arbitrary dimensions. From this formula we deduce the asymptotic behaviour of the volume of the zero cell as the dimension goes to ∞.

In this paper we develop a collection of results associated to the analysis of the sequential Monte Carlo (SMC) samplers algorithm, in the context of high-dimensional independent and identically distributed target probabilities. The SMC samplers algorithm can be designed to sample from a single probability distribution, using Monte Carlo to approximate expectations with respect to this law. Given a target density in d dimensions our results are concerned with d → ∞, while the number of Monte Carlo samples, N, remains fixed. 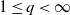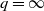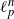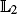We deduce an explicit bound on the Monte-Carlo error for estimates derived using the SMC sampler and the exact asymptotic relative -error of the estimate of the normalising constant associated to the target. We also establish marginal propagation of chaos properties of the algorithm. These results are deduced when the cost of the algorithm is O(Nd2).

Statistical inference for copulas has been addressed in various research papers. Due to the complicated theoretical results, studies have been carried out mainly in the bivariate case, be it properties of estimators or goodness-of-fit tests. However, from a practical point of view, higher dimensions are of interest. This work presents the results of large-scale simulation studies with particular focus on the question to what extent dimensionality influences point and interval estimators.