Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-05T08:24:52.039Z Has data issue: false hasContentIssue false
  • English
  • Français

Limit theorems for random points in a simplex

Part of: Geometric probability and stochastic geometry Limit theorems General convexity

Published online by Cambridge University Press:  21 June 2022

Anastas Baci ,
Zakhar Kabluchko ,
Joscha Prochno ,
Mathias Sonnleitner  and
Christoph Thäle
Anastas Baci*
Affiliation:
Ruhr University Bochum
Zakhar Kabluchko*
Affiliation:
University of Münster
Joscha Prochno*
Affiliation:
University of Graz and University of Passau
Mathias Sonnleitner*
Affiliation:
University of Graz and University of Passau
Christoph Thäle*
Affiliation:
Ruhr University Bochum
*
*Postal address: Faculty of Mathematics, Ruhr University Bochum, 44780 Bochum, Germany.
***Postal address: Faculty of Mathematics, University of Münster, 48149 Münster, Germany. Email: [email protected]
****Postal address: Institute of Mathematics and Scientific Computing, University of Graz, 8010 Graz, Austria.
****Postal address: Institute of Mathematics and Scientific Computing, University of Graz, 8010 Graz, Austria.
*Postal address: Faculty of Mathematics, Ruhr University Bochum, 44780 Bochum, Germany.
Get access Rights & Permissions [Opens in a new window]

Abstract

In this work the 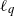$\ell_q$ -norms of points chosen uniformly at random in a centered regular simplex in high dimensions are studied. Berry–Esseen bounds in the regime 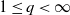$1\leq q < \infty$ are derived and complemented by a non-central limit theorem together with moderate and large deviations in the case where 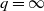$q=\infty$ . An application to the intersection volume of a regular simplex with an 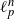$\ell_p^n$ -ball is also carried out.

Keywords

Berry–Esseen boundcentral limit theoremhigh dimensionsmoderate deviationsℓq-normlarge deviationsregular simplex

MSC classification

Primary: 60F05: Central limit and other weak theorems 60F10: Large deviations
Secondary: 52A23: Asymptotic theory of convex bodies 60D05: Geometric probability and stochastic geometry
Type
Original Article
Information
Journal of Applied Probability , Volume 59 , Issue 3 , September 2022 , pp. 685 - 701
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alonso-Gutiérrez, D., Prochno, J. and Thäle, C. (2018). Large deviations for high-dimensional random projections of $\ell_p^n$ -balls. Adv. Appl. Math. 99, 1–35.10.1016/j.aam.2018.04.003CrossRefGoogle Scholar
Alonso-Gutiérrez, D., Prochno, J. and Thäle, C. (2019). Gaussian fluctuations for high-dimensional random projections of $\ell_p^n$ -balls. Bernoulli 25, 3139–3174.10.3150/18-BEJ1084CrossRefGoogle Scholar
Alonso-Gutiérrez, D., Prochno, J. and Thäle, C. (2021). Large deviations, moderate deviations, and the KLS conjecture. J. Funct. Anal. 280, 108779.10.1016/j.jfa.2020.108779CrossRefGoogle Scholar
DasGupta, A., (2008). Asymptotic Theory of Statistics and Probability. Springer, New York.Google Scholar
David, H. A. and Nagaraja, H. N. (2003). Order Statistics, 3rd edn. Wiley-Interscience, Hoboken, NJ.10.1002/0471722162CrossRefGoogle Scholar
Dembo, A. and Zeitouni, O. (2010). Large Deviations Techniques and Applications, 2nd edn. Springer, Berlin.10.1007/978-3-642-03311-7CrossRefGoogle Scholar
Devroye, L. (1981). Laws of the iterated logarithm for order statistics of uniform spacings. Ann. Prob. 9, 860–867.10.1214/aop/1176994313CrossRefGoogle Scholar
Diaconis, P. and Freedman, D. (1987). A dozen de Finetti-style results in search of a theory. Ann. Inst. H. Poincaré Prob. Statist. 23, 397–423.Google Scholar
Does, R. J. M. M. and Klaassen, C. A. J. (1984). The Berry–Esseen theorem for functions of uniform spacings. Z. Wahrscheinlichkeitsth. 65, 461–471.10.1007/BF00533747CrossRefGoogle Scholar
Gantert, N., Kim, S. S. and Ramanan, K. (2016). Cramér’s theorem is atypical. In Advances in the Mathematical Sciences (Assoc. Women Math. Ser. 6), eds Letzter, G. et al. Springer, Cham, pp. 253–270.10.1007/978-3-319-34139-2_11CrossRefGoogle Scholar
Gantert, N. Kim, S. S. and Ramanan, K. (2017). Large deviations for random projections of $\ell^p$ balls. Ann. Prob. 45, 4419–4476.10.1214/16-AOP1169CrossRefGoogle Scholar
Giuliano, R. and Macci, C. (2014). Large deviation principles for sequences of maxima and minima. Commun. Statist. Theory Meth. 43, 1077–1098.10.1080/03610926.2012.668606CrossRefGoogle Scholar
Holst, L. (1979). Asymptotic normality of sum-functions of spacings. Ann. Prob. 7, 1066–1072.10.1214/aop/1176994901CrossRefGoogle Scholar
Johnston, S. G. G. and Prochno, J. (2019). Berry–Esseen bounds for random projections of $\ell_p^n$ -balls. Preprint, arXiv:1911.00695.Google Scholar
Kabluchko, Z., Prochno, J. and Thäle, C. (2019). High-dimensional limit theorems for random vectors in $\ell_p^n$ -balls. Commun. Contemp. Math. 21, 1750092.10.1142/S0219199717500924CrossRefGoogle Scholar
Kabluchko, Z., Prochno, J. and Thäle, C. (2020). Sanov-type large deviations in Schatten classes. Ann. Inst. Henri Poincaré Prob. Stat. 56, 928–953.10.1214/19-AIHP989CrossRefGoogle Scholar
Kabluchko, Z., Prochno, J. and Thäle, C. (2021). High-dimensional limit theorems for random vectors in $\ell_p^n$ -balls. II. Commun. Contemp. Math. 23, 1950073.Google Scholar
Kim, S. S. and Ramanan, K. (2018). A conditional limit theorem for high-dimensional $\ell^p$ -spheres. J. Appl. Prob. 55, 1060–1077.10.1017/jpr.2018.71CrossRefGoogle Scholar
Kim, S. S. and Ramanan, K. (2019). An asymptotic thin shell condition and large deviations for multidimensional projections. Preprint, arXiv:1912.13447.Google Scholar
Klartag, B. (2007). A central limit theorem for convex sets. Invent. Math. 168, 91–131.10.1007/s00222-006-0028-8CrossRefGoogle Scholar
Liao, Y.-T. and Ramanan, K. (2020). Geometric sharp large deviations for random projections of $\ell_p^n$ spheres. Preprint, arXiv:2001.04053.Google Scholar
Mathai, A. M. (1999). An Introduction to Geometrical Probability. Gordon and Breach, Amsterdam.Google Scholar
Mirakhmedov, S. A. (2005). Lower estimation of the remainder term in the CLT for a sum of the functions of k-spacings. Statist. Prob. Lett. 73, 411–424.10.1016/j.spl.2005.04.016CrossRefGoogle Scholar
Paouris, G., Pivovarov, P. and Zinn, J. (2014). A central limit theorem for projections of the cube. Prob. Theory Relat. Fields 159, 701–719.10.1007/s00440-013-0518-8CrossRefGoogle Scholar
Schechtman, G. and Schmuckenschläger, M. (1991). Another remark on the volume of the intersection of two $L^n_p$ balls. In Geometric Aspects of Functional Analysis (1989–90) (Lect. Notes Math. 1469), eds Lindenstrauss, J. and Milman, V. D.. Springer, Berlin, pp. 174–178.Google Scholar
Schechtman, G. and Zinn, J. (1990). On the volume of the intersection of two $L^n_p$ balls. Proc. Amer. Math. Soc. 110, 217–224.Google Scholar
Schmuckenschläger, M. (2001). CLT and the volume of intersections of $l^n_p$ -balls. Geom. Dedicata 85, 189–195.10.1023/A:1010353121014CrossRefGoogle Scholar
Vershynin, R. (2018). High-Dimensional Probability. Cambridge University Press.10.1017/9781108231596CrossRefGoogle Scholar