Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Beskos, Alexandros
Crisan, Dan
and
Jasra, Ajay
2014.
On the stability of sequential Monte Carlo methods in high dimensions.
The Annals of Applied Probability,
Vol. 24,
Issue. 4,
Kantas, Nikolas
Beskos, Alexandros
and
Jasra, Ajay
2014.
Sequential Monte Carlo Methods for High-Dimensional Inverse Problems: A Case Study for the Navier--Stokes Equations.
SIAM/ASA Journal on Uncertainty Quantification,
Vol. 2,
Issue. 1,
p.
464.
Rebeschini, Patrick
and
van Handel, Ramon
2015.
Can local particle filters beat the curse of dimensionality?.
The Annals of Applied Probability,
Vol. 25,
Issue. 5,
Beskos, Alexandros
Jasra, Ajay
Muzaffer, Ege A.
and
Stuart, Andrew M.
2015.
Sequential Monte Carlo methods for Bayesian elliptic inverse problems.
Statistics and Computing,
Vol. 25,
Issue. 4,
p.
727.
Saa, Pedro A.
and
Nielsen, Lars K.
2016.
Construction of feasible and accurate kinetic models of metabolism: A Bayesian approach.
Scientific Reports,
Vol. 6,
Issue. 1,
Saa, Pedro A.
and
Nielsen, Lars K.
2017.
Formulation, construction and analysis of kinetic models of metabolism: A review of modelling frameworks.
Biotechnology Advances,
Vol. 35,
Issue. 8,
p.
981.
Brosse, Nicolas
Durmus, Alain
and
Moulines, Éric
2018.
Normalizing constants of log-concave densities.
Electronic Journal of Statistics,
Vol. 12,
Issue. 1,
Dedecius, K.
2018.
Marginalized approximate filtering of state‐space models.
International Journal of Adaptive Control and Signal Processing,
Vol. 32,
Issue. 1,
p.
1.
Paulin, Daniel
Jasra, Ajay
and
Thiery, Alexandre
2019.
Error bounds for sequential Monte Carlo samplers for multimodal distributions.
Bernoulli,
Vol. 25,
Issue. 1,
Daviet, Remi
2019.
Sequential Optimal Inference for Experiments With Bayesian Particle Filters.
SSRN Electronic Journal ,
Jasra, Ajay
Law, Kody
and
Suciu, Carina
2020.
Advanced Multilevel Monte Carlo Methods.
International Statistical Review,
Vol. 88,
Issue. 3,
p.
548.
Park, Joonha
and
Ionides, Edward L.
2020.
Inference on high-dimensional implicit dynamic models using a guided intermediate resampling filter.
Statistics and Computing,
Vol. 30,
Issue. 5,
p.
1497.
Cotter, Colin
Crisan, Dan
Holm, Darryl D.
Pan, Wei
and
Shevchenko, Igor
2020.
A Particle Filter for Stochastic Advection by Lie Transport: A Case Study for the Damped and Forced Incompressible Two-Dimensional Euler Equation.
SIAM/ASA Journal on Uncertainty Quantification,
Vol. 8,
Issue. 4,
p.
1446.
Myers, Aaron
Thiéry, Alexandre H.
Wang, Kainan
and
Bui-Thanh, Tan
2021.
Sequential ensemble transform for Bayesian inverse problems.
Journal of Computational Physics,
Vol. 427,
Issue. ,
p.
110055.
Taghvaei, Amirhossein
and
Mehta, Prashant G.
2021.
Optimal Transportation Methods in Nonlinear Filtering.
IEEE Control Systems,
Vol. 41,
Issue. 4,
p.
34.
Ruzayqat, Hamza
Er-raiy, Aimad
Beskos, Alexandros
Crisan, Dan
Jasra, Ajay
and
Kantas, Nikolas
2022.
A Lagged Particle Filter for Stable Filtering of Certain High-Dimensional State-Space Models.
SIAM/ASA Journal on Uncertainty Quantification,
Vol. 10,
Issue. 3,
p.
1130.
Gutierrez, Rene
and
Guhaniyogi, Rajarshi
2022.
Bayesian Dynamic Feature Partitioning in High-Dimensional Regression With Big Data.
Technometrics,
Vol. 64,
Issue. 2,
p.
224.
Taghvaei, Amirhossein
and
Hosseini, Bamdad
2022.
An Optimal Transport Formulation of Bayes’ Law for Nonlinear Filtering Algorithms.
p.
6608.
Oliveira, Rafael
Scalzo, Richard
Kohn, Robert
Cripps, Sally
Hardman, Kyle
Close, John
Taghavi, Nasrin
and
Lemckert, Charles
2022.
Bayesian optimization with informative parametric models via sequential Monte Carlo.
Data-Centric Engineering,
Vol. 3,
Issue. ,
Taghvaei, Amirhossein
and
Mehta, Prashant G.
2023.
A survey of feedback particle filter and related controlled interacting particle systems (CIPS).
Annual Reviews in Control,
Vol. 55,
Issue. ,
p.
356.
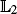 -error of the estimate of the normalising constant associated to the target. We also establish marginal propagation of chaos properties of the algorithm. These results are deduced when the cost of the algorithm is O(Nd2).
-error of the estimate of the normalising constant associated to the target. We also establish marginal propagation of chaos properties of the algorithm. These results are deduced when the cost of the algorithm is O(Nd2).