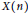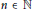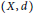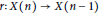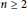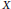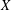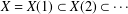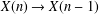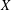2 results
Lipschitz Retractions in Hadamard Spaces via Gradient Flow Semigroups
-
- Journal:
- Canadian Mathematical Bulletin / Volume 59 / Issue 4 / 01 December 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 673-681
- Print publication:
- 01 December 2016
-
- Article
-
- You have access
- Export citation
-
Let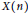
$X\left( n \right)$, for 
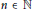$n\,\in \,\mathbb{N}$, be the set of all subsets of a metric space 
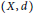$\left( x,\,d \right)$ of cardinality at most 
$n$. The set 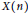$X\left( n \right)$ equipped with the Hausdorff metric is called a finite subset space. In this paper we are concerned with the existence of Lipschitz retractions 
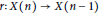$r:\,X\left( n \right)\,\to \,X\left( n\,-\,1 \right)$ for 
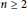$n\,\ge \,2$. It is known that such retractions do not exist if 
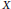$X$ is the one-dimensional sphere. On the other hand, Kovalev has recently established their existence if 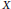$X$ is a Hilbert space, and he also posed a question as to whether or not such Lipschitz retractions exist when 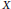$X$ is a Hadamard space. In this paper we answer the question in the positive.
LIPSCHITZ RETRACTION OF FINITE SUBSETS OF HILBERT SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 08 July 2015, pp. 146-151
- Print publication:
- February 2016
-
- Article
-
- You have access
- Export citation
-
Finite subset spaces of a metric space
$X$ form a nested sequence under natural isometric embeddings 
$X=X(1)\subset X(2)\subset \cdots \,$. We prove that this sequence admits Lipschitz retractions 
$X(n)\rightarrow X(n-1)$ when 
$X$ is a Hilbert space.
