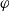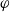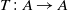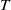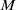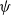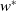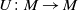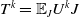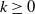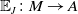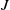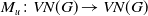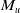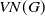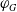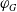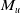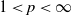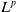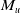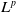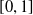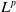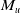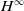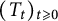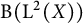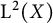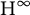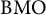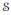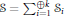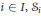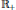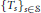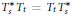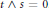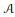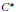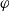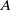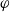Let $\varphi$ be a normal semifinite faithful weight on a von Neumann algebra $A$, let $(\sigma ^\varphi _r)_{r\in {\mathbb R}}$ denote the modular automorphism group of $\varphi$, and let 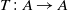$T\colon A\to A$ be a linear map. 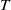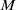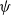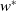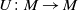We say that $T$ admits an absolute dilation if there exists another von Neumann algebra $M$ equipped with a normal semifinite faithful weight $\psi$, a $w^*$-continuous, unital and weight-preserving $*$-homomorphism $J\colon A\to M$ such that $\sigma ^\psi \circ J=J\circ \sigma ^\varphi$, as well as a weight-preserving $*$-automorphism $U\colon M\to M$ such that 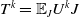$T^k={\mathbb {E}}_JU^kJ$ for all integer 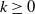$k\geq 0$, where 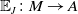$ {\mathbb {E}}_J\colon M\to A$ is the conditional expectation associated with 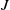$J$. Given any locally compact group $G$ and any real valued function $u\in C_b(G)$, we prove that if $u$ induces a unital completely positive Fourier multiplier 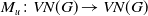$M_u\colon VN(G) \to VN(G)$, then 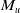$M_u$ admits an absolute dilation. Here, 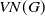$VN(G)$ is equipped with its Plancherel weight 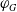$\varphi _G$. This result had been settled by the first named author in the case when $G$ is unimodular so the salient point in this paper is that $G$ may be nonunimodular, and hence, 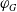$\varphi _G$ may not be a trace. The absolute dilation of 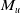$M_u$ implies that for any 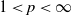$1\lt p\lt \infty$, the 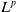$L^p$-realization of 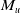$M_u$ can be dilated into an isometry acting on a noncommutative 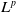$L^p$-space. We further prove that if $u$ is valued in 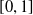$[0,1]$, then the 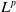$L^p$-realization of 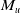$M_u$ is a Ritt operator with a bounded 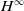$H^\infty$-functional calculus.

Using probabilistic tools, we prove that any weak* continuous semigroup $(T_t)_{t \geqslant 0}$ of self-adjoint unital completely positive measurable Schur multipliers acting on the space $\mathrm {B}({\mathrm {L}}^2(X))$ of bounded operators on the Hilbert space ${\mathrm {L}}^2(X)$, where X is a suitable measure space, can be dilated by a weak* continuous group of Markov $*$-automorphisms on a bigger von Neumann algebra. We also construct a Markov dilation of these semigroups. Our results imply the boundedness of the McIntosh’s ${\mathrm {H}}^\infty $ functional calculus of the generators of these semigroups on the associated Schatten spaces and some interpolation results connected to ${\mathrm {BMO}}$-spaces. We also give an answer to a question of Steen, Todorov, and Turowska on completely positive continuous Schur multipliers.

Let $S$ be the semigroup $S=\sum\nolimits_{i=1}^{\oplus k}{{{S}_{i}}}$, where for each $i\in I,{{S}_{i}}$ is a countable subsemigroup of the additive semigroup ${{\mathbb{R}}_{+}}$ containing 0. We consider representations of $S$ as contractions ${{\left\{ {{T}_{s}} \right\}}_{s\in S}}$ on a Hilbert space with the Nica-covariance property: $T_{s}^{*}{{T}_{t}}={{T}_{t}}T_{s}^{*}$ whenever $t\wedge s=0$. We show that all such representations have a unique minimal isometric Nica-covariant dilation.

This result is used to help analyse the nonself-adjoint semicrossed product algebras formed from Nica-covariant representations of the action of $S$ on an operator algebra $\mathcal{A}$ by completely contractive endomorphisms. We conclude by calculating the ${{C}^{*}}$-envelope of the isometric nonself-adjoint semicrossed product algebra (in the sense of Kakariadis and Katsoulis).