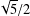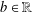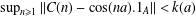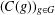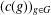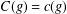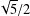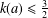2 results
A ZERO-
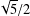 $\!\sqrt{5}/2$
LAW FOR COSINE FAMILIES
$\!\sqrt{5}/2$
LAW FOR COSINE FAMILIES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 104 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 17 April 2017, pp. 195-217
- Print publication:
- April 2018
-
- Article
-
- You have access
- Export citation
ON COSINE FAMILIES CLOSE TO SCALAR COSINE FAMILIES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 99 / Issue 2 / October 2015
- Published online by Cambridge University Press:
- 26 February 2015, pp. 166-174
- Print publication:
- October 2015
-
- Article
-
- You have access
- Export citation