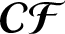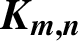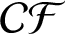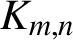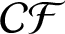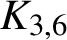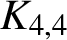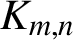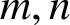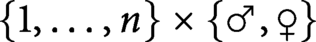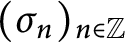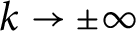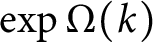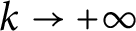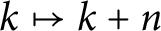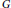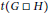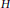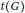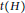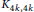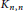3 results
ON PROBLEMS OF
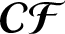 $\boldsymbol{\mathcal{CF}}$
-CONNECTED GRAPHS FOR
$\boldsymbol{\mathcal{CF}}$
-CONNECTED GRAPHS FOR
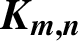 $\boldsymbol{K}_{\boldsymbol{m,n}}$
$\boldsymbol{K}_{\boldsymbol{m,n}}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 01 December 2020, pp. 203-210
- Print publication:
- October 2021
-
- Article
- Export citation
Mallows permutations as stable matchings
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 27 July 2020, pp. 1531-1555
- Print publication:
- December 2021
-
- Article
-
- You have access
- Open access
- Export citation
The Thickness of the Cartesian Product of Two Graphs
-
- Journal:
- Canadian Mathematical Bulletin / Volume 59 / Issue 4 / 01 December 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 705-720
- Print publication:
- 01 December 2016
-
- Article
-
- You have access
- Export citation