Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-22T20:28:18.299Z Has data issue: false hasContentIssue false
  • English
  • Français

The Thickness of the Cartesian Product of Two Graphs

Published online by Cambridge University Press:  20 November 2018

Yichao Chen  and
Xuluo Yin
Yichao Chen
Affiliation:
Department of Mathematics, Hunan University, 410082 Changsha, China e-mail: [email protected] e-mail: [email protected]
Xuluo Yin
Affiliation:
Department of Mathematics, Hunan University, 410082 Changsha, China e-mail: [email protected] e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The thickness of a graph 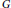$G$ is the minimum number of planar subgraphs whose union is 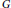$G$. A $t$-minimal graph is a graph of thickness $t$ that contains no proper subgraph of thickness $t$. In this paper, upper and lower bounds are obtained for the thickness, 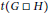$t\left( G\,\square \,H \right)$, of the Cartesian product of two graphs 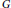$G$ and 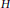$H$, in terms of the thickness 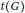$t\left( G \right)$ and 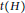$t\left( H \right)$. Furthermore, the thickness of the Cartesian product of two planar graphs and of a $t$-minimal graph and a planar graph are determined. By using a new planar decomposition of the complete bipartite graph 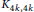${{K}_{4k,\,4k}}$, the thickness of the Cartesian product of two complete bipartite graphs 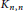${{K}_{n,n}}$ and 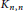${{K}_{n,n}}$ is also given for 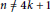$n\,\ne \,4k\,+\,1$.

Keywords

05C10planar graphthicknessCartesian productt-minimal graphcomplete bipartite graph
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 59 , Issue 4 , 01 December 2016 , pp. 705 - 720
Copyright
Copyright © Canadian Mathematical Society 2016

References

[1] Aggarwal, A., Klawe, M., and Shor, P., Multilayer grid embeddings for VLSI. Algorithmica 6(1991), no. 1, 129–151. http://dx.doi.Org/10.1007/BF01759038 Google Scholar
[2] Alekseev, V. B. and Gonchakov, V. S., Thickness of arbitrary complete graphs. Mat. Sb. 101(143)(1976), no. 2, 212–230.Google Scholar
[3] Behzad, M. and Mahmoodian, S. E., On topological invariants of the product of graphs. Canad. Math. Bull. 12(1969), 157–166. http://dx.doi.Org/10.4153/CMB-1969-015-9 Google Scholar
[4] Beineke, L. W. and Harary, R., The thickness of the complete graph. Canad. J. Math. 17(1965), 850–859. http://dx.doi.Org/10.4153/CJM-1965-084-2 Google Scholar
[5] Beineke, L. W., Harary, E., and Moon, J. W., On the thickness of the complete bipartite graph. Proc. Cambridge Philos. Soc. 60(1964), 1–5. http://dx.doi.Org/!0.1017/S0305004100037385 Google Scholar
[6] Boutin, D. L., Gethner, E., and Sulanke, T., Thickness-two graphs part one: New nine-critical graphs, permuted layer graphs, and Catlin's graphs. J. Graph Theory 57(2008), no. 3,198-214. http://dx.doi.Org/10.1002/jgt.20282 Google Scholar
[7] Bouwer, I. Z. and Broere, I., Note on t-minimal complete bipartite graphs. Canad. Math. Bull. 11(1968), 729–732. http://dx.doi.Org/10.4153/CMB-1968-088-x Google Scholar
[8] Hobbs, A. M. and Grossman, J. W., Thickness and connectivity in graphs. J. Res. Nat. Bur. Standards Sect B 72B(1968), 239–244. http://dx.doi.Org/10.6028/jres.072B.023 Google Scholar
[9] Imrich, W., Klavzar, S., and Rail, D. F., Topics in graph theory: graphs and their Cartesian product. A. K. Peters, Wellesley, MA, 2008.Google Scholar
[10] Kleinert, M., Die Dicke des n-dimensionalen Wurfel-Graphen. J. Combin. Theory 3(1967), 10–15. http://dx.doi.Org/10.1016/SOO21-9800(67)80010-3 Google Scholar
[11] Mansfield, A., Determining the thickness of graphs is NP-hard. Math. Proc. Cambridge Philos. Soc. 93(1983), no. 1, 9–23. http://dx.doi.Org/10.1017/S030500410006028X Google Scholar
[12] Mutzel, P., Odenthal, T., and Scharbrodt, M., The thickness of a graph: a survey. Graphs Combin. 14(1998), no. 1, 59–73. http://dx.doi.Org/10.1007/PL00007219 Google Scholar
[13] Pisanski, T., Genus of cartesian products of regular bipartite graphs. J. Graph Theory 4(1980), no. 1, 31–42. http://dx.doi.Org/10.1OO2/jgt.3190040105 Google Scholar
[14] Širáň, J. and Horák, Peter , A construction of thickness-minimal graphs. Discrete Math. 64(1987), no. 2-3, 263–268. http://dx.doi.Org/10.1016/0012-365X(87)90195-6 Google Scholar
[15] Tutte, W. T., The thickness of a graph. Indag. Math. 25(1963), 567–577. http://dx.doi.Org/10.1016/S1385-7258(63)50055-9 Google Scholar
[16] Vasak, J. M., The thickness of the complete graph. Ph.D. thesis, University of Illinois at Urbana-Champaign, 1976.Google Scholar
[17] White, A. T., The genus of the Cartesian product of two graphs. J. Combin. Theory Ser. B 11(1971), 89–94. http://dx.doi.Org/10.1016/0095-8956(71)90018-9 Google Scholar
[18] Yang, Y., A note on the thickness of Kl, m, n. Ars Combin. 117(2014), 349–351.Google Scholar
[19] Yang, Y. and Chen, Y., The thickness of amalgamations and cartesian product of graphs. Discuss. Math. Graph. Theory, to appear.Google Scholar