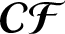Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-23T05:25:12.693Z Has data issue: false hasContentIssue false
  • English
  • Français

ON PROBLEMS OF $\boldsymbol{\mathcal{CF}}$-CONNECTED GRAPHS FOR 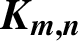$\boldsymbol{K}_{\boldsymbol{m,n}}$

Part of: Algebraic combinatorics Discrete mathematics in relation to computer science

Published online by Cambridge University Press:  01 December 2020

MICHAL STAŠ Open the ORCID record for MICHAL STAŠ [Opens in a new window]  and
JURAJ VALISKA Open the ORCID record for JURAJ VALISKA [Opens in a new window]
MICHAL STAŠ*
Affiliation:
Department of Mathematics and Theoretical Informatics, Faculty of Electrical Engineering and Informatics, Technical University of Košice, Letná 9, 042 00Košice, Slovak Republic
JURAJ VALISKA
Affiliation:
Department of Mathematics and Theoretical Informatics, Faculty of Electrical Engineering and Informatics, Technical University of Košice, Letná 9, 042 00 Košice, Slovak Republic e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A connected graph G is 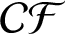$\mathcal {CF}$ -connected if there is a path between every pair of vertices with no crossing on its edges for each optimal drawing of G. We conjecture that a complete bipartite graph 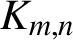$K_{m,n}$ is 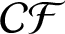$\mathcal {CF}$ -connected if and only if it does not contain a subgraph of 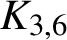$K_{3,6}$ or 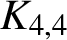$K_{4,4}$ . We establish the validity of this conjecture for all complete bipartite graphs 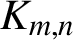$K_{m,n}$ for any 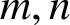$m,n$ with 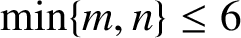$\min \{m,n\}\leq 6$ , and conditionally for 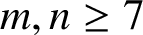$m,n\geq 7$ on the assumption of Zarankiewicz’s conjecture that 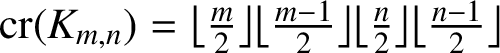$\mathrm {cr}(K_{m,n})=\big \lfloor \frac {m}{2} \big \rfloor \big \lfloor \frac {m-1}{2} \big \rfloor \big \lfloor \frac {n}{2} \big \rfloor \big \lfloor \frac {n-1}{2} \big \rfloor $ .

Keywords

complete bipartite graphcrossing numbercrossing sequenceoptimal drawing

MSC classification

Primary: 05E30: Association schemes, strongly regular graphs
Secondary: 68R10: Graph theory (including graph drawing)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 104 , Issue 2 , October 2021 , pp. 203 - 210
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bokal, D. and Leaños, J., ‘Characterizing all graphs with $2$ -exceptional edges’, Ars Math. Contemp. 15(2) (2018), 383–406.CrossRefGoogle Scholar
Cairns, G., Mendan, S. and Nikolayevsky, Y., ‘A sufficient condition for a pair of sequences to be bipartite graphic’, Bull. Aust. Math. Soc. 94(2) (2016), 195–200.CrossRefGoogle Scholar
Christian, R., Richter, R. B. and Salazar, G., ‘Zarankiewicz’s conjecture is finite for each fixed $m$ ’, J. Combin. Theory Ser. B 103(2) (2013), 237–247.CrossRefGoogle Scholar
Guy, R. K., ‘The decline and fall of Zarankiewicz’s theorem’, in: Proof Techniques in Graph Theory (ed. Harary, F.) (Academic Press, New York, 1969), 63–69.Google Scholar
Kleitman, D. J., ‘The crossing number of ${K}_{5,n}$ ’, J. Combin. Theory 9 (1970), 315–323.CrossRefGoogle Scholar
Klešč, M., ‘The crossing number of join of the special graph on six vertices with path and cycle’, Discrete Math. 310(9) (2010), 1475–1481.CrossRefGoogle Scholar
Norin, S. and Zwols, Y., ‘Turan’s brickyard problem and flag algebras’, BIRS Workshop on Geometric and Topological Graph Theory, 2013 (presentation 13w5091), available online at http://www.birs.ca/events/2013/5-day-workshops/13w5091/videos/watch/201310011538-Norin.html.Google Scholar
Woodall, D. R., ‘Cyclic-order graphs and Zarankiewicz’s crossing number conjecture’, J. Graph Theory 17(6) (1993), 657–671.CrossRefGoogle Scholar
Zarankiewicz, K., ‘On a problem of P. Turan concerning graphs’, Fund. Math. 41(1) (1955), 137–145.CrossRefGoogle Scholar