Let K$K$ be a subgroup of a finite group G$G$. The probability that an element of G$G$ commutes with an element of K$K$ is denoted by Pr(K,G)$Pr(K,G)$. Assume that Pr(K,G)\geq \epsilon$Pr(K,G)\geq \epsilon$ for some fixed \epsilon >0$\epsilon >0$. We show that there is a normal subgroup T\leq G$T\leq G$ and a subgroup B\leq K$B\leq K$ such that the indices [G:T]$[G:T]$ and [K:B]$[K:B]$ and the order of the commutator subgroup [T,B]$[T,B]$ are \epsilon$\epsilon$-bounded. This extends the well-known theorem, due to P. M. Neumann, that covers the case where K=G$K=G$. We deduce a number of corollaries of this result. A typical application is that if K$K$ is the generalized Fitting subgroup F^{*}(G)$F^{*}(G)$ then G$G$ has a class-2-nilpotent normal subgroup R$R$ such that both the index [G:R]$[G:R]$ and the order of the commutator subgroup [R,R]$[R,R]$ are \epsilon$\epsilon$-bounded. In the same spirit we consider the cases where K$K$ is a term of the lower central series of G$G$, or a Sylow subgroup, etc.

The commutativity degree of a finite group is the probability that two randomly chosen group elements commute. The object of this paper is to compute the commutativity degree of a class of finite groups obtained by semidirect product of two finite abelian groups. As a byproduct of our result, we provide an affirmative answer to an open question posed by Lescot.

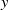In a recent article [K. H. Hofmann and F. G. Russo, ‘The probability that x$x$ and y$y$ commute in a compact group’, Math. Proc. Cambridge Phil Soc., to appear] we calculated for a compact group 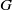G$G$ the probability 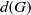d(G)$d(G)$ that two randomly selected elements 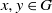x, y\in G$x, y\in G$ satisfy xy=yx$xy=yx$, and we discussed the remarkable consequences on the structure of 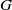G$G$ which follow from the assumption that 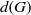d(G)$d(G)$ is positive. In this note we consider two natural numbers 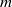m$m$ and n$n$ and the probability 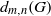d_{m,n}(G)$d_{m,n}(G)$ that for two randomly selected elements 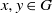x, y\in G$x, y\in G$ the relation 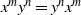x^my^n=y^nx^m$x^my^n=y^nx^m$ holds. The situation is more complicated whenever 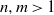n,m\gt 1$n,m\gt 1$. If 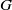G$G$ is a compact Lie group and if its identity component 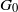G_0$G_0$ is abelian, then it follows readily that 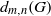d_{m,n}(G)$d_{m,n}(G)$ is positive. 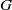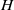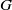We show here that the following condition suffices for the converse to hold in an arbitrary compact group G$G$: for any nonopen closed subgroup H$H$ of G$G$, the sets 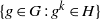\{g\in G: g^k\in H\}$\{g\in G: g^k\in H\}$ for both 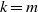k=m$k=m$ and 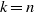k=n$k=n$ have Haar measure 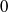0$0$. Indeed, we show that if a compact group 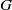G$G$ satisfies this condition and if 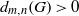d_{m,n}(G)\gt 0$d_{m,n}(G)\gt 0$, then the identity component of 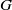G$G$is abelian.

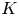
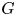
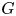
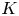
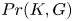
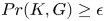
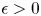
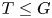
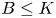
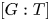
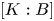
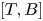
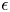
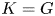
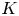
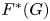
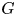
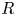
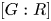
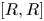
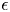
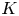
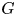
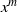
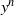
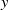
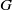
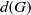
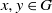
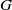
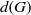
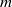
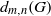
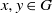
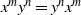
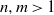
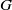
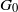
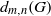
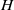
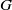
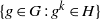
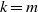
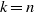
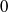
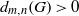
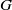
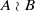We compute commutativity degrees of wreath products of finite Abelian groups A and B. When B is fixed of order n the asymptotic commutativity degree of such wreath products is 1/n2. This answers a generalized version of a question posed by P. Lescot. As byproducts of our formula we compute the number of conjugacy classes in such wreath products, and obtain an interesting elementary number-theoretic result.