2 results
AN ELEMENTARY PROOF OF JAMES’ CHARACTERISATION OF WEAK COMPACTNESS. II
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 26 September 2016, pp. 133-137
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
Complemented Copies of ℓ1 and Pełczyński's Property (V*) in Bochner Function Spaces
-
- Journal:
- Canadian Journal of Mathematics / Volume 48 / Issue 3 / 01 June 1996
- Published online by Cambridge University Press:
- 20 November 2018, pp. 625-640
- Print publication:
- 01 June 1996
-
- Article
-
- You have access
- Export citation
-
Let X be a Banach space and (fn)n be a bounded sequence in L1(X). We prove a complemented version of the celebrated Talagrand's dichotomy, i.e., we show that if (en)n denotes the unit vector basis of c0, there exists a sequence gn ∈ conv(fn, fn+1,...) such that for almost every ω, either the sequence (gn(ω) ⊗ en) is weakly Cauchy in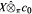
or it is equivalent to the unit vector basis of ℓ1. We then get a criterion for a bounded sequence to contain a subsequence equivalent to a complemented copy of ℓ1 in L1(X). As an application, we show that for a Banach space X, the space L1(X) has Pełczyńiski's property (V*) if and only if X does.
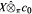or it is equivalent to the unit vector basis of 