Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-26T15:52:37.833Z Has data issue: false hasContentIssue false
  • English
  • Français

Complemented Copies of ℓ1 and Pełczyński's Property (V*) in Bochner Function Spaces

Published online by Cambridge University Press:  20 November 2018

Narcisse Randrianantoanina
Narcisse Randrianantoanina*
Affiliation:
Department of Mathematics The University of Texas at Austin Austin, Texas 78712 U.S.A. email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let X be a Banach space and (fn)n be a bounded sequence in L1(X). We prove a complemented version of the celebrated Talagrand's dichotomy, i.e., we show that if (en)n denotes the unit vector basis of c0, there exists a sequence gn ∈ conv(fn, fn+1,...) such that for almost every ω, either the sequence (gn(ω) ⊗ en) is weakly Cauchy in 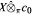or it is equivalent to the unit vector basis of ℓ1. We then get a criterion for a bounded sequence to contain a subsequence equivalent to a complemented copy of ℓ1 in L1(X). As an application, we show that for a Banach space X, the space L1(X) has Pełczyńiski's property (V*) if and only if X does.

Keywords

46E4028B0528B20Weakly compact setsBochner function spaces
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 48 , Issue 3 , 01 June 1996 , pp. 625 - 640
Copyright
Copyright © Canadian Mathematical Society 1996

References

1. Bombal, F., On (V*) sets andPelczynski'sproperty (V*), Glasgow Math. J. 32 (1990), 109–120.Google Scholar
2. Cembranos, P., Kalton, N.J., Saab, E., and Saab, P., Pelczynski's Property (V) on C(Q,E) spaces, Math. Ann. 271 (1985), 91–97.Google Scholar
3. Cohn, D.L.,Measure Theory, Birkhäuser, Basel, Stuttgart, 1980.Google Scholar
4. Debs, G., Effective properties in compact sets of Borel functions, Mathematika 34 (1987), 64–68.Google Scholar
5. Diestel, J., Sequences and Series in Banach Spaces, Graduate Texts in Math. 92, Springer Verlag, New York, first edition, 1984.Google Scholar
6. Diestel, J. and Jr. Uhl, J.J., Vector Measures, Math Surveys 15, Amer. Math. Soc, Providence, Rhode Island, 1977.Google Scholar
7. Diestel, J., Ruess, W.M., and Schachermayer, W., Weak compactness in Ll(μ,X), Proc. Amer. Math. Soc. 118 (1993), 447–453.Google Scholar
8. Emmanuele, G., On the Banach spaces with the property (V*) of Pelczyński, Ann. Mat. Pura Appl. 152 (1988), 171–181.Google Scholar
9. Godefroy, G. and Saab, P., Quelques espaces de Banach ay ant les proprietes (V) ou (V*) de A. Pelczynski, C.R. Acad. Sci. Paris Sér. 1303 (1986), 503–506.Google Scholar
10. Heinrich, R. and Mankiewicz, P., Applications of ultrapowers to the uniform and Lipschitz classification of Banach spaces, Studia Math. 73 (1982), 225–251.Google Scholar
11. Leung, D., Property (V*) in the space of Bochner-integrable functions, Rev. Roumaine Math. Pures Appl. 35 (1990), 147–150.Google Scholar
12. Lindenstrauss, J. and Tzafriri, L., ClassicalBanach spaces II, Modern Survey In Math. 97 Springer-Verlag, Berlin, Heidelberg, New York, first edition, 1979.Google Scholar
13. Pelczynski, A., On Banach spaces on which every unconditionally converging operator is weakly compact, Bull. Acad. Polon. Sci. 10 (1962), 641–648.Google Scholar
14. Pfitzner, H., L-summands in their biduals have Pelczynski's property (F*), Studia Math. 104 (1993), 91–98.Google Scholar
15. Rosenthal, H.P., A characterization of Banach spaces containing ℓ1, Proc. Nat. Acad. Sci. U.S.A. 71 (1974), 2411–2413.Google Scholar
16. Saab, E. and Saab, P., On Pelczynski's properties (V) and(V*), Pacific J. Math. 125 (1986), 205–210.Google Scholar
17. Talagrand, M., Quand Vespace des mesures a variation borneé est-il faiblement sequentiellement complet?, Proc. Amer. Math. Soc. 99 (1984), 285–288.Google Scholar
18. Talagrand, M., Weak Cauchy sequences in LX﹛E), Amer. J. Math. 106 (1984), 703–724.Google Scholar
19. Wojtaszczyk, P., Banach spaces for analysts, Cambridge Univ. Press, first edition, 1991.Google Scholar