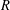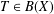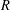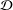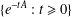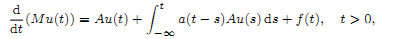5 results
NEW COUNTEREXAMPLES ON RITT OPERATORS, SECTORIAL OPERATORS AND
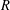 $R$-BOUNDEDNESS
$R$-BOUNDEDNESS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 3 / December 2019
- Published online by Cambridge University Press:
- 11 April 2019, pp. 498-506
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
On functional calculus properties of Ritt operators
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 145 / Issue 6 / December 2015
- Published online by Cambridge University Press:
- 26 November 2015, pp. 1239-1250
- Print publication:
- December 2015
-
- Article
- Export citation
Maximal regularity for degenerate differential equations with infinite delay in periodic vector-valued function spaces
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 3 / October 2013
- Published online by Cambridge University Press:
- 21 August 2013, pp. 853-871
-
- Article
-
- You have access
- Export citation
TENSOR EXTENSION PROPERTIES OF C(K)-REPRESENTATIONS AND APPLICATIONS TO UNCONDITIONALITY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 88 / Issue 2 / April 2010
- Published online by Cambridge University Press:
- 11 March 2010, pp. 205-230
- Print publication:
- April 2010
-
- Article
-
- You have access
- Export citation
Products of commuting Boolean algebras of projections and Banach space geometry
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 91 / Issue 2 / September 2005
- Published online by Cambridge University Press:
- 23 August 2005, pp. 483-508
- Print publication:
- September 2005
-
- Article
- Export citation