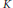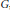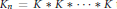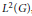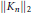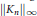1 results
Some Conditions for Decay of Convolution Powers and Heat Kernels on Groups
-
- Journal:
- Canadian Journal of Mathematics / Volume 57 / Issue 6 / 01 December 2005
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1193-1214
- Print publication:
- 01 December 2005
-
- Article
-
- You have access
- Export citation
-
Let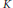
$K$ be a function on a unimodular locally compact group 
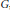$G$, and denote by 
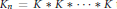${{K}_{n}}\,=\,K\,*\,K\,*\cdots *\,K$ the 
$n$-th convolution power of 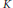$K$. Assuming that 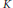$K$ satisfies certain operator estimates in 
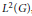${{L}^{2}}\left( G \right)$, we give estimates of the norms 
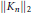${{\left\| {{K}_{n}} \right\|}_{2}}$ and 
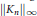${{\left\| {{K}_{n}} \right\|}_{\infty }}$ for large $n$. In contrast to previous methods for estimating 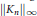${{\left\| {{K}_{n}} \right\|}_{\infty }}$, we do not need to assume that the function 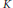$K$ is a probability density or nonnegative. Our results also adapt for continuous time semigroups on 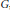$G$. Various applications are given, for example, to estimates of the behaviour of heat kernels on Lie groups.
