Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-23T20:04:02.987Z Has data issue: false hasContentIssue false
  • English
  • Français

Some Conditions for Decay of Convolution Powers and Heat Kernels on Groups

Published online by Cambridge University Press:  20 November 2018

Nick Dungey
Nick Dungey*
Affiliation:
School of Mathematics, The University of New South Wales, Sydney 2052 Australia, e-mail address: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 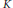$K$ be a function on a unimodular locally compact group 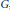$G$, and denote by 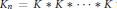${{K}_{n}}\,=\,K\,*\,K\,*\cdots *\,K$ the $n$-th convolution power of 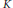$K$. Assuming that 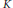$K$ satisfies certain operator estimates in 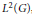${{L}^{2}}\left( G \right)$, we give estimates of the norms 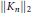${{\left\| {{K}_{n}} \right\|}_{2}}$ and 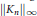${{\left\| {{K}_{n}} \right\|}_{\infty }}$ for large $n$. In contrast to previous methods for estimating 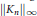${{\left\| {{K}_{n}} \right\|}_{\infty }}$, we do not need to assume that the function 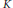$K$ is a probability density or nonnegative. Our results also adapt for continuous time semigroups on 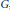$G$. Various applications are given, for example, to estimates of the behaviour of heat kernels on Lie groups.

Keywords

Primary: 22E30secondary: 35B4043A99
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 57 , Issue 6 , 01 December 2005 , pp. 1193 - 1214
Copyright
Copyright © Canadian Mathematical Society 2005

References

[1] Auscher, P., ter Elst, A. F. M. and Robinson, D.W., On positive Rockland operators. Colloq. Math. 67(1994), 197–216.Google Scholar
[2] Coulhon, T., Ultracontractivity and Nash type inequalities. J. Funct. Anal. 141(1996), 510–539.Google Scholar
[3] Davies, E B., Heat Kernels and Spectral Theory. Cambridge Tracts in Mathematics 92, Cambridge University Press, Cambridge, 1989.Google Scholar
[4] Davies, E B., Long time asymptotics of fourth order parabolic equations. J. Anal.Math. 67(1995), 323–345.Google Scholar
[5] Davies, E B., Lp spectral theory of higher-order elliptic differential operators. Bull. LondonMath. Soc. 29(1997), 513–546.Google Scholar
[6] Dungey, N., Higher order operators and Gaussian bounds on Lie groups of polynomial growth. J. Operator Theory 46(2001), 45–61.Google Scholar
[7] Dungey, N., ter Elst, A. F. M. and Robinson, D.W., On anomalous asymptotics of heat kernels on groups of polynomial growth. Mathematics Research Report 01-006, The Australian National University, 2001.Google Scholar
[8] Dungey, N., ter Elst, A. F. M. and Robinson, D.W., Analysis on Lie GroupsWith Polynomial Growth. Progress in Mathematics 214, Birkhäuser, Boston,MA, 2003.Google Scholar
[9] Dungey, N., ter Elst, A. F. M., Robinson, D.W. and Adam, Sikora, Asymptotics of subcoercive semigroups on nilpotent Lie groups. J. Operator Theory 45(2001), 81–110.Google Scholar
[10] Dziubanski, J., Hebisch, W. and Zienkiewicz, J., Note on semigroups generated by positive Rockland operators on graded homogeneous groups. Studia Math. 110(1994), 115–126.Google Scholar
[11] ter Elst, A. F. M. and Robinson, D.W., Weighted subcoercive operators on Lie groups. J. Funct. Anal. 157(1998), 88–163.Google Scholar
[12] ter Elst, A. F. M. and Robinson, D.W., On anomalous asymptotics of heat kernels. In: Evolution Equations and Their Applications To Physical and Life Sciences, Lecture Notes in Pure and Appl. Math. 215, Dekker, New York, 2001, pp. 89–103.Google Scholar
[13] ter Elst, A. F. M. and Robinson, D.W. Gaussian bounds for complex subelliptic operators on Lie groups of polynomial growth. Bull. Austral. Math. Soc. 67(2003), 201–218.Google Scholar
[14] ter Elst, A. F. M., Robinson, D.W. and Sikora, A., Heat kernels and Riesz transforms on nilpotent Lie groups. Colloq. Math. 74(1997), 191–218.Google Scholar
[15] Guivarc’h, Y., Croissance polynomiale et périodes des fonctions harmoniques. Bull. Soc. Math. France 101(1973), 333–379.Google Scholar
[16] Hebisch, W., Estimates on the semigroups generated by left invariant operators on Lie groups. J. Reine Angew.Math. 423(1992), 1–45.Google Scholar
[17] Hebisch, W. and Saloff-Coste, L., Gaussian estimates for Markov chains and random walks on groups. Ann. Probab. 21(1993), 673–709.Google Scholar
[18] Kato, T., Perturbation theory for linear operators. Grundlehren der mathematischen Wissenschaften 132, Springer-Verlag, Berlin, 1984.Google Scholar
[19] Nagel, A., Ricci, F., and Stein, E. M., Harmonic analysis and fundamental solutions on nilpotent Lie groups. In: Analysis and Partial Differential Equations, Lecture Notes in Pure and Applied Mathematics 122, Dekker, New York, 1990, 249–275.Google Scholar
[20] Nagel, A., Stein, E. M., and S.Wainger, Balls and metrics defined by vector fields. I: basic properties. Acta Math. 155(1985), 103–147.Google Scholar
[21] Robinson, D.W., Elliptic operators and Lie groups. Oxford Mathematical Monographs, Oxford University Press, Oxford, 1991.Google Scholar
[22] Saloff-Coste, L., Probability on groups: random walks and invariant diffusions. Notices Amer.Math. Soc. 48(2001), 968–977.Google Scholar
[23] Varopoulos, N. T., Convolution powers on locally compact groups. Bull. Sci. Math. 111(1987), 333–342.Google Scholar
[24] Varopoulos, N. T., Analysis on Lie groups. Rev.Mat. Iberoamericana 12(1996), 791–917.Google Scholar
[25] Varopoulos, N. T., Saloff-Coste, L., and Coulhon, T., Analysis and Geometry on Groups. Cambridge Tracts in Mathematics 100, Cambridge University Press, Cambridge, 1992.Google Scholar