16 results
Chapter 4 - Scenario Building
-
- Book:
- Handbook of Augmented Reality Training Design Principles
- Published online:
- 18 May 2023
- Print publication:
- 01 June 2023, pp 34-49
-
- Chapter
- Export citation
New semi-analytical calculation of lunar, solar and planetary perturbations in motion of Earth satellites
-
- Journal:
- Proceedings of the International Astronomical Union / Volume 18 / Issue S382 / December 2022
- Published online by Cambridge University Press:
- 16 October 2024, pp. 142-145
- Print publication:
- December 2022
-
- Article
-
- You have access
- Export citation
4 - Norms and Matrix Conditioning
- from Part I - Numerical Linear Algebra
-
- Book:
- Classical Numerical Analysis
- Published online:
- 29 September 2022
- Print publication:
- 20 October 2022, pp 73-87
-
- Chapter
- Export citation
Approximations of geometrically ergodic reversible markov chains
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 22 November 2021, pp. 981-1022
- Print publication:
- December 2021
-
- Article
- Export citation
Perturbations of Von Neumann Subalgebras With Finite Index
-
- Journal:
- Canadian Mathematical Bulletin / Volume 59 / Issue 2 / 01 June 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 320-325
- Print publication:
- 01 June 2016
-
- Article
-
- You have access
- Export citation
Complements to the longitudinal librations of an elastic 3-layer Titan on a non-Keplerian orbit
-
- Journal:
- Proceedings of the International Astronomical Union / Volume 9 / Issue S310 / July 2014
- Published online by Cambridge University Press:
- 05 January 2015, pp. 21-24
- Print publication:
- July 2014
-
- Article
-
- You have access
- Export citation
C*–algebras Nearly Contained in Type I Algebras
-
- Journal:
- Canadian Journal of Mathematics / Volume 65 / Issue 1 / 01 February 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 52-65
- Print publication:
- 01 February 2013
-
- Article
-
- You have access
- Export citation
The decay of a swirling perturbation of pipe Poiseuille flow
-
- Journal:
- European Journal of Applied Mathematics / Volume 23 / Issue 3 / June 2012
- Published online by Cambridge University Press:
- 12 January 2012, pp. 373-394
-
- Article
- Export citation
Perturbations of Multipliers of Systems of Periodic Ordinary Differential Equations
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 3 / Issue 5 / October 2011
- Published online by Cambridge University Press:
- 03 June 2015, pp. 562-571
- Print publication:
- October 2011
-
- Article
- Export citation
BASIC FUNCTIONAL ANALYSIS PUZZLES OF SPECTRAL FLOW
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 90 / Issue 2 / April 2011
- Published online by Cambridge University Press:
- 19 July 2011, pp. 145-154
- Print publication:
- April 2011
-
- Article
-
- You have access
- Export citation
Fish communities of a perturbed stream in Southern Nigeria
-
- Journal:
- Journal of Tropical Ecology / Volume 4 / Issue 1 / February 1988
- Published online by Cambridge University Press:
- 10 July 2009, pp. 49-59
-
- Article
- Export citation
Amélioration du transfert thermique par optimisation de la géométrie d'une conduite de révolution
-
- Journal:
- Mechanics & Industry / Volume 6 / Issue 2 / March 2005
- Published online by Cambridge University Press:
- 21 April 2005, pp. 189-193
- Print publication:
- March 2005
-
- Article
- Export citation
Additive results for the generalized Drazin inverse
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 73 / Issue 1 / August 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 115-126
- Print publication:
- August 2002
-
- Article
-
- You have access
- Export citation
Truncation approximations of invariant measures for Markov chains
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 35 / Issue 3 / September 1998
- Published online by Cambridge University Press:
- 14 July 2016, pp. 517-536
- Print publication:
- September 1998
-
- Article
- Export citation
Perturbation theory for Markov reward processes with applications to queueing systems
-
- Journal:
- Advances in Applied Probability / Volume 20 / Issue 1 / March 1988
- Published online by Cambridge University Press:
- 01 July 2016, pp. 79-98
- Print publication:
- March 1988
-
- Article
- Export citation
The robustness of positive recurrence and recurrence of Markov chains under perturbations of the transition probabilities
-
- Journal:
- Journal of Applied Probability / Volume 12 / Issue 4 / December 1975
- Published online by Cambridge University Press:
- 14 July 2016, pp. 744-752
- Print publication:
- December 1975
-
- Article
- Export citation

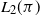
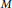
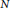
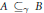


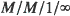 ). Extensions to Markov decision processes and other settings are discussed.
). Extensions to Markov decision processes and other settings are discussed.