Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-23T12:12:19.524Z Has data issue: false hasContentIssue false
  • English
  • Français

Approximations of geometrically ergodic reversible markov chains

Part of: Probabilistic methods, simulation and stochastic differential equations Markov processes

Published online by Cambridge University Press:  22 November 2021

Jeffrey Negrea Open the ORCID record for Jeffrey Negrea [Opens in a new window]  and
Jeffrey S. Rosenthal Open the ORCID record for Jeffrey S. Rosenthal [Opens in a new window]
Jeffrey Negrea*
Affiliation:
University of Toronto
Jeffrey S. Rosenthal*
Affiliation:
University of Toronto
*
*Postal address: Department of Statistical Sciences, 9th Floor, 700 University Ave., Toronto, ON M5G 1Z5, Canada.
*Postal address: Department of Statistical Sciences, 9th Floor, 700 University Ave., Toronto, ON M5G 1Z5, Canada.
Get access Rights & Permissions [Opens in a new window]

Abstract

A common tool in the practice of Markov chain Monte Carlo (MCMC) is to use approximating transition kernels to speed up computation when the desired kernel is slow to evaluate or is intractable. A limited set of quantitative tools exists to assess the relative accuracy and efficiency of such approximations. We derive a set of tools for such analysis based on the Hilbert space generated by the stationary distribution we intend to sample, 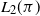$L_2(\pi)$. Our results apply to approximations of reversible chains which are geometrically ergodic, as is typically the case for applications to MCMC. The focus of our work is on determining whether the approximating kernel will preserve the geometric ergodicity of the exact chain, and whether the approximating stationary distribution will be close to the original stationary distribution. For reversible chains, our results extend the results of Johndrow et al. (2015) from the uniformly ergodic case to the geometrically ergodic case, under some additional regularity conditions. We then apply our results to a number of approximate MCMC algorithms.

Keywords

Markov chainMonte Carloperturbations

MSC classification

Primary: 60J05: Discrete-time Markov processes on general state spaces
Secondary: 60J22: Computational methods in Markov chains 65C05: Monte Carlo methods
Type
Original Article
Information
Advances in Applied Probability , Volume 53 , Issue 4 , December 2021 , pp. 981 - 1022
Check for updates
Copyright
© The Author(s) 2021. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alquier, P., Friel, N., Everitt, R. and Boland, A. (2016). Noisy Monte Carlo: convergence of Markov chains with approximate transition kernels. Statist. Comput. 26, 29–47.CrossRefGoogle Scholar
Andrieu, C. and Roberts, G. O. (2009). The pseudo-marginal approach for efficient Monte Carlo computations. Ann. Statist. 37, 697–725.CrossRefGoogle Scholar
Baxendale, P. H. (2005). Renewal theory and computable convergence rates for geometrically ergodic Markov chains. Ann. Appl. Prob. 15, 700–738.CrossRefGoogle Scholar
Baxter, J. R. and Rosenthal, J. S. (1995). Rates of convergence for everywhere-positive Markov chains. Statist. Prob. Lett. 22, 333–338.CrossRefGoogle Scholar
Breslow, N. E. and Clayton, D. G. (1993). Approximate inference in generalized linear mixed models. J. Amer. Statist. Assoc. 88, 9–25.Google Scholar
Breyer, L., Roberts, G. and Rosenthal, J. A note on geometric ergodicity and floating-point roundoff error. Statist. Prob. Lett. 53, 123–127.CrossRefGoogle Scholar
Brooks, S., Gelmand, A., Jones, G. L. and Meng, X.-L. (eds) (2011). Handbook of Markov Chain Monte Carlo. Chapman and Hall, Boca Raton, FL.CrossRefGoogle Scholar
Campbell, T. and Broderick, T. (2019). Automated scalable Bayesian inference via Hilbert coresets. J. Mach. Learning Res. 20, 551–588.Google Scholar
Douc, R., Moulines, E., Priouret, P. and Soulier, P. (2018). Markov Chains. Springer, Cham.CrossRefGoogle Scholar
Ferré, D., Hervé, L. and Ledoux, J. (2013). Regular perturbation of V-geometrically ergodic Markov chains. J. Appl. Prob. 50, 184–194.CrossRefGoogle Scholar
Gibbs, A. (2004). Convergence in the Wasserstein metric for Markov chain Monte Carlo algorithms with applications to image restoration. Stoch. Models 20, 473–492.CrossRefGoogle Scholar
Hervé, L. and Ledoux, J. (2014). Approximating Markov chains and V-geometric ergodicity via weak perturbation theory. Stoch. Process. Appl. 124, 613–638.CrossRefGoogle Scholar
Hobert, J. P. and Geyer, C. J. (1998). Geometric ergodicity of Gibbs and block Gibbs samplers for a hierarchical random effects model. J. Multivariate Anal. 67, 414–430.CrossRefGoogle Scholar
Huggins, J., Campbell, T. and Broderick, T. (2016). Coresets for scalable Bayesian logistic regression. In Advances in Neural Information Processing Systems 29 (NIPS 2016), eds Lee, D. et al., NIPS, Barcelona, pp. 4080–4088.Google Scholar
Jain, N. and Jamison, B. (1967). Contributions to Doeblin’s theory of Markov processes. Prob. Theory Relat. Fields 8, 19–40.Google Scholar
Johndrow, J. E. and Mattingly, J. C. (2017). Coupling and decoupling to bound an approximating Markov chain. Preprint. Available at https://arxiv.org/abs/1706.02040.Google Scholar
Johndrow, J. E. and Mattingly, J. C. (2017). Error bounds for approximations of Markov chains used in Bayesian sampling. Preprint. Available at https://arxiv.org/abs/1711.05382.Google Scholar
Johndrow, J. E., Mattingly, J. C., Mukherjee, S. and Dunson, D. (2015). Approximations of Markov chains and high-dimensional Bayesian inference. Preprint. Available at https://arxiv.org/abs/1508.03387v1.Google Scholar
Kass, R. E., Tierney, L. and Kadane, J. B. (1990). The validity of posterior expansions based on Laplace’s method. In Bayesian and Likelihood Methods in Statistics and Econometrics, Elsevier, Amsterdam, pp. 473–488.Google Scholar
Keller, G. and Liverani, C. (1999). Stability of the spectrum for transfer operators. Ann. Scuola Norm. Sci. 28, 141–152.Google Scholar
Liu, J. S. (2008). Monte Carlo Strategies in Scientific Computing. Springer, New York.Google Scholar
Livingstone, S., Betancourt, M., Byrne, S. and Girolami, M. (2019). On the geometric ergodicity of Hamiltonian Monte Carlo. Bernoulli 25, 3109–3138.CrossRefGoogle Scholar
McCulloch, C. E. and Neuhaus, J. M. (2005). Generalized linear mixed models. In Encyclopedia of Biostatistics, eds Armitage, P. and Colton, T., Wiley, John, York, New. Available at https://doi.org/10.1002/0470011815.b2a10021.CrossRefGoogle Scholar
Medina-Aguayo, F., Rudolf, D. and Schweizer, N. (2019). Perturbation bounds for Monte Carlo within Metropolis via restricted approximations. Stoch. Process. Appl. 130, 2200–2227.CrossRefGoogle Scholar
Medina-Aguayo, F. J., Lee, A. and Roberts, G. O. (2016). Stability of noisy Metropolis–Hastings. Statist. Comput. 26, 1187–1211.CrossRefGoogle ScholarPubMed
Mitrophanov, A. Y. (2005). Sensitivity and convergence of uniformly ergodic Markov chains. J. Appl. Prob. 42, 1003–1014.CrossRefGoogle Scholar
Nummelin, E. and Tweedie, R. L. (1978). Geometric ergodicity and R-positivity for general Markov chains. Ann. Prob. 6, 404–420.CrossRefGoogle Scholar
Pillai, N. S. and Smith, A. (2014). Ergodicity of approximate MCMC chains with applications to large data sets. Preprint. Available at https://arxiv.org/abs/1405.0182.Google Scholar
Roberts, G. O. and Rosenthal, J. S. (1997). Geometric ergodicity and hybrid Markov chains. Electron. Commun. Prob. 2, 13–25.CrossRefGoogle Scholar
Roberts, G. O. and Rosenthal, J. S. (2004). General state space Markov chains and MCMC algorithms. Prob. Surveys 1, 20–71.CrossRefGoogle Scholar
Roberts, G. O., Rosenthal, J. S. and Schwartz, P. O. (1998). Convergence properties of perturbed Markov chains. J. Appl. Prob. 35, 1–11.CrossRefGoogle Scholar
Roberts, G. O. and Tweedie, R. L. (2001). Geometric $L^2$ and $L^1$ convergence are equivalent for reversible Markov chains. J. Appl. Prob. 38, 37–41.Google Scholar
Rudin, W. (1991). Functional Analysis, 2nd edn. McGraw-Hill, New York.Google Scholar
Rudolf, D. (2011). Explicit error bounds for Markov chain Monte Carlo. Dissertationes Math. 485, 93 pp. Available at https://arxiv.org/abs/1108.3201.Google Scholar
Rudolf, D. and Schweizer, N. (2015). Perturbation theory for Markov chains via Wasserstein distance. Preprint. Available at https://arxiv.org/abs/1503.04123.Google Scholar
Smith, R. L. and Tierney, L. (1996). Exact transition probabilities for the independence Metropolis sampler. Available at http://www.rls.sites.oasis.unc.edu/postscript/rs/exact.pdf.Google Scholar
Tierney, L. and Kadane, J. B. (1986). Accurate approximations for posterior moments and marginal densities. J. Amer. Statist. Assoc. 81, 82–86.CrossRefGoogle Scholar