We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
The paper is concerned with positive solutions to problems of the type\[ -\Delta_{\mathbb{B}^{N}} u - \lambda u = a(x) |u|^{p-1}\;u + f \text{ in }\mathbb{B}^{N}, \quad u \in H^{1}{(\mathbb{B}^{N})}, \]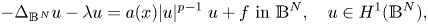where $\mathbb {B}^N$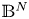
denotes the hyperbolic space, $1< p<2^*-1:=\frac {N+2}{N-2}$
, $\;\lambda < \frac {(N-1)^2}{4}$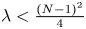
, and $f \in H^{-1}(\mathbb {B}^{N})$
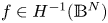($f \not \equiv 0$
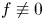) is a non-negative functional. The potential $a\in L^\infty (\mathbb {B}^N)$
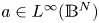is assumed to be strictly positive, such that $\lim _{d(x, 0) \rightarrow \infty } a(x) \rightarrow 1,$
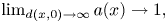where $d(x,\, 0)$
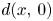denotes the geodesic distance. First, the existence of three positive solutions is proved under the assumption that $a(x) \leq 1$
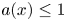. Then the case $a(x) \geq 1$
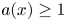is considered, and the existence of two positive solutions is proved. In both cases, it is assumed that $\mu ( \{ x : a(x) \neq 1\}) > 0.$
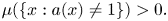Subsequently, we establish the existence of two positive solutions for $a(x) \equiv 1$
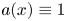and prove asymptotic estimates for positive solutions using barrier-type arguments. The proofs for existence combine variational arguments, key energy estimates involving hyperbolic bubbles.
