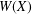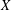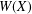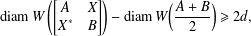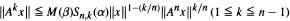3 results
NUMERICAL RANGE AND POSITIVE BLOCK MATRICES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 11 June 2020, pp. 69-77
- Print publication:
- February 2021
-
- Article
- Export citation
THE NORM OF THE PRODUCT OF POLYNOMIALS IN INFINITE DIMENSIONS
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 49 / Issue 1 / February 2006
- Published online by Cambridge University Press:
- 02 February 2006, pp. 17-28
-
- Article
-
- You have access
- Export citation
Norm Inequalities for Generators of Analytic Semigroups and Cosine Operator Functions
-
- Journal:
- Canadian Mathematical Bulletin / Volume 32 / Issue 1 / 01 March 1989
- Published online by Cambridge University Press:
- 20 November 2018, pp. 47-53
- Print publication:
- 01 March 1989
-
- Article
-
- You have access
- Export citation