 $p$ local Langlands correspondence
$p$ local Langlands correspondence
 $\operatorname { {GL}}_n$ OVER p-ADIC FIELDS
$\operatorname { {GL}}_n$ OVER p-ADIC FIELDS
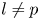 $l \neq p$
$l \neq p$
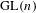 $\text{GL}(n)$ AND THE LOCAL JACQUET–LANGLANDS CORRESPONDENCE
$\text{GL}(n)$ AND THE LOCAL JACQUET–LANGLANDS CORRESPONDENCE
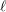 $\ell$ -blocs de niveau zéro des groupes
$\ell$ -blocs de niveau zéro des groupes 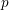 $p$ -adiques
$p$ -adiques
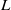 -packets
-packets