No CrossRef data available.
Article contents
An Iwahori theoretic mod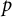 
$p$ local Langlands correspondence
Published online by Cambridge University Press: 17 February 2025
Abstract
We extend a comparison theorem of Anandavardhanan–Borisagar between the quotient of the induction of a mod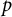 
$p$ character by the image of an Iwahori–Hecke operator and compact induction of a weight to the case of the trivial character. This involves studying the corresponding non-commutative Iwahori–Hecke algebra. We use this to give an Iwahori theoretic reformulation of the (semi-simple) mod 
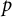$p$ local Langlands correspondence discovered by Breuil and reformulated functorially by Colmez. This version of the correspondence is expected to have applications to computing the mod 
$p$ reductions of semi-stable Galois representations.
MSC classification
Primary:
20G05: Representation theory
- Type
- Article
- Information
- Copyright
- © The Author(s), 2025. Published by Cambridge University Press on behalf of Canadian Mathematical Society
References
Anandavardhanan, U. K. and Borisagar, G. H.,
On the
$K(n)$
-invariants of a supersingular representation of
$GL_2(\mathbb{Q}_p)$
. In: B. C. Berndt and D. Prasad (eds.), The legacy of Srinivasa Ramanujan, Ramanujan Mathematical Society Lecture Notes Series, 20, Ramanujan Mathematical Society, Mysore, 2013, pp. 55–75.Google Scholar
$K(n)$
-invariants of a supersingular representation of
$GL_2(\mathbb{Q}_p)$
. In: B. C. Berndt and D. Prasad (eds.), The legacy of Srinivasa Ramanujan, Ramanujan Mathematical Society Lecture Notes Series, 20, Ramanujan Mathematical Society, Mysore, 2013, pp. 55–75.Google ScholarAnandavardhanan, U. K. and Borisagar, G. H.,
Iwahori-Hecke model for supersingular representations of
$GL_2(\mathbb{Q}_p)$
. J. Algebra 423(2015), 1–27. https://doi.org/10.1016/j.jalgebra.2014.10.003.CrossRefGoogle Scholar
$GL_2(\mathbb{Q}_p)$
. J. Algebra 423(2015), 1–27. https://doi.org/10.1016/j.jalgebra.2014.10.003.CrossRefGoogle ScholarAnandavardhanan, U. K. and Jana, A., Iwahori-Hecke model for
$\mathit{{mod}}\;p$
representations of
$GL\left(2,F\right)$
. Pacific J. Math. 315(2021), no. 2, 255–283. https://doi.org/10.2140/pjm.2021.315.255.CrossRefGoogle Scholar
$\mathit{{mod}}\;p$
representations of
$GL\left(2,F\right)$
. Pacific J. Math. 315(2021), no. 2, 255–283. https://doi.org/10.2140/pjm.2021.315.255.CrossRefGoogle ScholarArsovski, B.,
On the reductions of certain two-dimensional crystalline representations
. Doc. Math. 26(2021), 1929–1979. https://doi.org/10.4171/dm/861.CrossRefGoogle Scholar
Barthel, L. and Livné, R., Irreducible modular representations of
$GL_2$
of a local field
. Duke Math. J. 75(1994), no. 2, 261–292. https://doi.org/10.1215/S0012-7094-94-07508-X.Google Scholar
$GL_2$
of a local field
. Duke Math. J. 75(1994), no. 2, 261–292. https://doi.org/10.1215/S0012-7094-94-07508-X.Google ScholarBarthel, L. and Livné, R., Modular representations of
$GL_2$
of a local field: The ordinary, unramified case
. J. Number Theory 55(1995), no. 1, 1–27. https://doi.org/10.1006/jnth.1995.1124.CrossRefGoogle Scholar
$GL_2$
of a local field: The ordinary, unramified case
. J. Number Theory 55(1995), no. 1, 1–27. https://doi.org/10.1006/jnth.1995.1124.CrossRefGoogle ScholarBerger, L., Représentations modulaires de
$GL_2\left(\boldsymbol{Q}_p\right)$
et représentations galoisiennes de dimension 2
. Astérisque 330(2010), 263–279.Google Scholar
$GL_2\left(\boldsymbol{Q}_p\right)$
et représentations galoisiennes de dimension 2
. Astérisque 330(2010), 263–279.Google ScholarBhattacharya, S. and Ghate, E.,
Reductions of Galois representations for slopes in
$\left(1,2\right)$
. Doc. Math. 20(2015), 943–987. https://doi.org/10.4171/dm/510.CrossRefGoogle Scholar
$\left(1,2\right)$
. Doc. Math. 20(2015), 943–987. https://doi.org/10.4171/dm/510.CrossRefGoogle ScholarBhattacharya, S., Ghate, E., and Rozensztajn, S.,
Reductions of Galois representations of slope 1
. J. Algebra 508(2018), 98–156. https://doi.org/10.1016/j.jalgebra.2018.04.023.CrossRefGoogle Scholar
Breuil, C.,
Sur quelques représentations modulaires et
$p$
-adiques de
$GL_2(\boldsymbol{Q}_p)$
.
$I$
. Compos. Math. 138(2003), no. 2, 165–188. https://doi.org/10.1023/A:1026191928449.CrossRefGoogle Scholar
$p$
-adiques de
$GL_2(\boldsymbol{Q}_p)$
.
$I$
. Compos. Math. 138(2003), no. 2, 165–188. https://doi.org/10.1023/A:1026191928449.CrossRefGoogle ScholarBreuil, C.,
Sur quelques représentations modulaires et
$p$
-adiques de
$GL_2(\boldsymbol{Q}_p)$
. II
. J. Inst. Math. Jussieu 2(2003), no. 1, 23–58. https://doi.org/10.1017/S1474748003000021.CrossRefGoogle Scholar
$p$
-adiques de
$GL_2(\boldsymbol{Q}_p)$
. II
. J. Inst. Math. Jussieu 2(2003), no. 1, 23–58. https://doi.org/10.1017/S1474748003000021.CrossRefGoogle ScholarBreuil, C.,
The emerging
$p$
-adic Langlands programme. In: Proceedings of the international congress of mathematicians. Vol II, Hindustan Book Agency, New Delhi, 2010, pp. 203–230. https://doi.org/10.1142/9789814324359_0047.Google Scholar
$p$
-adic Langlands programme. In: Proceedings of the international congress of mathematicians. Vol II, Hindustan Book Agency, New Delhi, 2010, pp. 203–230. https://doi.org/10.1142/9789814324359_0047.Google ScholarBuzzard, K. and Gee, T., Explicit reduction modulo
$p$
of certain two-dimensional crystalline representations
. Int. Math. Res. Not. IMRN 12(2009), 2303–2317. https://doi.org/10.1093/imrn/rnp017.Google Scholar
$p$
of certain two-dimensional crystalline representations
. Int. Math. Res. Not. IMRN 12(2009), 2303–2317. https://doi.org/10.1093/imrn/rnp017.Google ScholarBuzzard, K. and Gee, T., Explicit reduction modulo
$p$
of certain 2-dimensional crystalline representations, II
. Bull. Lond. Math. Soc. 45(2013), no. 4, 779–788. https://doi.org/10.1112/blms/bds128.CrossRefGoogle Scholar
$p$
of certain 2-dimensional crystalline representations, II
. Bull. Lond. Math. Soc. 45(2013), no. 4, 779–788. https://doi.org/10.1112/blms/bds128.CrossRefGoogle ScholarChitrao, A. and Ghate, E., Reductions of semi-stable representations using the Iwahori mod
$p$
Local Langlands Correspondence. Submitted, 2024.Google Scholar
$p$
Local Langlands Correspondence. Submitted, 2024.Google ScholarColmez, P., Représentations de
$GL2\left(\boldsymbol{Q}p\right)$
et
$\left(\phi, \varGamma \right)$
-modules
. Astérisque 330(2010), 281–509.Google Scholar
$GL2\left(\boldsymbol{Q}p\right)$
et
$\left(\phi, \varGamma \right)$
-modules
. Astérisque 330(2010), 281–509.Google ScholarGanguli, A. and Ghate, E., Reductions of Galois representations via the
$\mathit{{mod}}\;p$
local Langlands correspondence
. J. Number Theory 147(2015), 250–286. https://doi.org/10.1016/j.jnt.2014.07.011.CrossRefGoogle Scholar
$\mathit{{mod}}\;p$
local Langlands correspondence
. J. Number Theory 147(2015), 250–286. https://doi.org/10.1016/j.jnt.2014.07.011.CrossRefGoogle ScholarGhate, E.,
A zig-zag conjecture and local constancy for Galois representations
. In: Algebraic number theory and related topics 2018. Vol. B86. RIMS Kôkyûroku Bessatsu, Research Institute for Mathematical Sciences (RIMS), Kyoto, 2021, pp. 249–268.Google Scholar
Ghate, E. and Jana, A., Modular representations of
$GL_2(F_q)$
using calculus. Forum Mathematicum (2024) To appear.Google Scholar
$GL_2(F_q)$
using calculus. Forum Mathematicum (2024) To appear.Google ScholarGhate, E. and Rai, V.,
Reductions of Galois representations of slope
$\frac{3}{2}$
. Kyoto J. Math. (2023). To appear.Google Scholar
$\frac{3}{2}$
. Kyoto J. Math. (2023). To appear.Google ScholarJana, A.,
The pro-
$p$
-Iwahori invariants of the universal quotient representation for
$GL_2(F)$
. Int. J. Number Theory 19(2023), no. 8, 1853–1879. https://doi.org/10.1142/S1793042123500896.
CrossRefGoogle Scholar
$p$
-Iwahori invariants of the universal quotient representation for
$GL_2(F)$
. Int. J. Number Theory 19(2023), no. 8, 1853–1879. https://doi.org/10.1142/S1793042123500896.
CrossRefGoogle ScholarMorra, S.,
Invariant elements for
$p$
-modular representations of
$\boldsymbol{GL}_2\left(\boldsymbol{Q}_p\right)$
. Trans. Amer. Math. Soc. 365(2013), no. 12, 6625–6667. https://doi.org/10.1090/S0002-9947-2013-05932-6.
CrossRefGoogle Scholar
$p$
-modular representations of
$\boldsymbol{GL}_2\left(\boldsymbol{Q}_p\right)$
. Trans. Amer. Math. Soc. 365(2013), no. 12, 6625–6667. https://doi.org/10.1090/S0002-9947-2013-05932-6.
CrossRefGoogle ScholarNagel, E. and Pande, A., Reductions of modular Galois representations of Slope (2,3). Preprint, 2019.Google Scholar