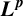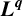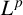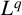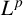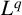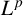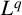6 results
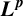 $\boldsymbol {L}^{\boldsymbol {p}}$–
$\boldsymbol {L}^{\boldsymbol {p}}$–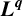 $\boldsymbol {L}^{\boldsymbol {q}}$ MULTIPLIERS ON COMMUTATIVE HYPERGROUPS
$\boldsymbol {L}^{\boldsymbol {q}}$ MULTIPLIERS ON COMMUTATIVE HYPERGROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 115 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 18 October 2023, pp. 375-395
- Print publication:
- December 2023
-
- Article
- Export citation
Exact Solutions for the Flow of Fractional Maxwell Fluid in Pipe-Like Domains
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 8 / Issue 5 / October 2016
- Published online by Cambridge University Press:
- 08 July 2016, pp. 784-794
- Print publication:
- October 2016
-
- Article
- Export citation
Frictionless Contact of a Functionally Graded Half-Space and a rigid Base with an Axially Symmetric Recess
-
- Journal:
- Journal of Mechanics / Volume 25 / Issue 1 / March 2009
- Published online by Cambridge University Press:
- 05 May 2011, pp. 9-18
- Print publication:
- March 2009
-
- Article
- Export citation
Laplace Transform Type Multipliers for Hankel Transforms
-
- Journal:
- Canadian Mathematical Bulletin / Volume 51 / Issue 4 / 01 December 2008
- Published online by Cambridge University Press:
- 20 November 2018, pp. 487-496
- Print publication:
- 01 December 2008
-
- Article
-
- You have access
- Export citation
Hankel Convolution Operators on Spaces of Entire Functions of Finite Order
-
- Journal:
- Canadian Mathematical Bulletin / Volume 48 / Issue 2 / 01 June 2005
- Published online by Cambridge University Press:
- 20 November 2018, pp. 161-174
- Print publication:
- 01 June 2005
-
- Article
-
- You have access
- Export citation
The application of the Hankel transformation to spherically symmetric coverage problems
-
- Journal:
- Journal of Applied Probability / Volume 17 / Issue 4 / December 1980
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1121-1126
- Print publication:
- December 1980
-
- Article
- Export citation