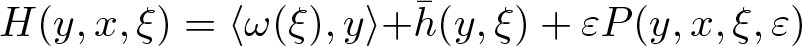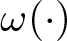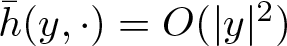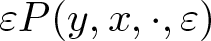1 results
Kolmogorov’s theorem for degenerate Hamiltonian systems with Hölder continuous parameters
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 26 November 2024, pp. 1-36
-
- Article
-
- You have access
- HTML
- Export citation
-
In this paper, we investigate Kolmogorov-type theorems for small perturbations of degenerate Hamiltonian systems. These systems are index by a parameter ξ as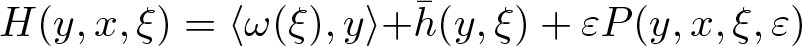
$ H(y,x,\xi) = \langle\omega(\xi),y\rangle {+ \bar h(y,\xi)}+\varepsilon P(y,x,\xi,\varepsilon) $, where ɛ > 0. We assume that the frequency mapping 
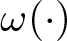$\omega(\cdot)$, 
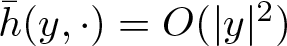$\bar h(y,\cdot)=O(|y|^2)$ and the perturbation 
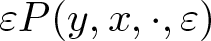$\varepsilon P(y,x,\cdot, \varepsilon)$ maintain Hölder continuity about ξ. We prove that the persistent invariant tori retain the same frequency as those of the unperturbed tori, under a certain topological degree condition and a weak convexity condition for the frequency mapping. Notably, this paper presents, to our understanding, pioneering results on the KAM theorem under such conditions with only assumption of Hölder continuous dependence of frequency mapping ω on the parameter.
