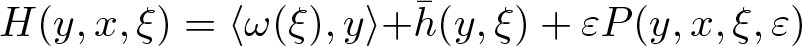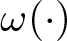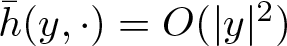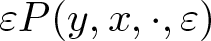1. Introduction
As a conservation law of energy, Hamiltonian systems are frequently considered to describe models arose in celestial mechanics or the motion of charged particles in magnetic fields, see [Reference Chierchia8, Reference Meyer24, Reference Wayne38].
The classical KAM theory, as presented by Arnold, Kolmogorov, and Moser [Reference Arnold1, Reference Kolmogorov20, Reference Moser25], posits that under the Kolmogorov non-degenerate condition, most invariant tori of an integrable Hamiltonian system can withstand small perturbations. While these tori might undergo minor deformations, they transform into other invariant tori that retain the original frequency.
Numerous methods have been explored to study the persistence of invariant tori and the preservation of toral frequency within Hamiltonian systems under certain non-degenerate conditions. For instance, the KAM approach was used in [Reference Benettin, Galgant, Giorgilli and Strelcyn2, Reference Bounemoura4, Reference de la Llave, González, Jorba and Villanueva12, Reference Li and Yi22, Reference Pöschel30, Reference Salamon35]. The direct method using Lindstedt series can be found in references [Reference Chierchia and Falcolini9, Reference Eliasson13, Reference Gallavotti15], while renormalization group techniques were discussed in [Reference Bricmont, Gawedzki and Kupiainen5, Reference Gallavotti, Gentile and Mastropietro16]. Notably, the study presented in [Reference Chow, Li and Yi10] introduced the idea of partial preservation of unperturbed frequencies and delved into the persistence problem on a specified smooth sub-manifold for real analytic Hamiltonian systems, particularly under the Rüssmann-like non-degenerate condition. For insights under analogous conditions, see also [Reference Sevryuk37].
Yet, in the context of persistence, two fundamental questions emerge that warrant attention:
Q1: In the event of a failure in the Kolmogorov non-degenerate condition, can the invariant tori with the same frequency still be preserved under small perturbations?
Q2: If the regularity of the frequency mapping diminishes to mere continuity, can the aforementioned result withstand small perturbations?
To shed light on these questions, we review previous findings and offer a more comprehensive overview.
1.1. Degeneracy
Consider the real analytic nearly integrable Hamiltonian system
where x is the angle variable in the standard torus ![]() $\mathbb{T}^{n}$,
$\mathbb{T}^{n}$, ![]() $n\geq2$ refers to the dimension; y is the action variable in a bounded closed region
$n\geq2$ refers to the dimension; y is the action variable in a bounded closed region ![]() $G\subset \mathbb{R}^n$, and ɛ > 0 is a small parameter.
$G\subset \mathbb{R}^n$, and ɛ > 0 is a small parameter.
A fundamental assumption in historical research is the Kolmogorov non-degenerate condition. However, if we assume that there exists a ![]() $y_0\in G$ such that:
$y_0\in G$ such that:
 \begin{align*}
\det\frac{\partial^2h(y_0)}{\partial y^2}=0,
\end{align*}
\begin{align*}
\det\frac{\partial^2h(y_0)}{\partial y^2}=0,
\end{align*}then the Kolmogorov non-degenerate condition is not satisfied. The spatial solar system serves as a prominent example of this situation, as detailed in [Reference Féjoz14]. Naturally, a question arises: does the persistence result still stand under these conditions? This question has been a primary motivation for this research.
In fact, even under weaker non-degenerate conditions, KAM tori might not preserve their frequencies. As demonstrated in [Reference Brjuno6, Reference Rüssmann34, Reference Sevryuk36], under the Brjuno non-degenerate condition and Rüssmann non-degenerate condition, the presumption of an unchanged frequency may not necessarily hold true. This is because the frequency of perturbed tori can undergo slight variations. Similar observations are noted in [Reference Biasco, Chierchia and Treschev3, Reference Cheng and Sun7, Reference Chow, Li and Yi10, Reference Cong, Küpper, Li and You11, Reference Heinz18, Reference Qian, Li and Yang32, Reference Xu, You and Qiu40]. Consequently, deriving conditions that assure the persistence of frequencies for KAM tori in the context of a degenerate Hamiltonian becomes rather challenging. Furthermore, the issue of the perturbed invariant tori maintaining a consistent frequency has seldom been tackled for degenerate systems.
1.2. Regularity
On the matter of regularity, it is worth noting the distinctions in the studies of various researchers. Kolmogorov [Reference Kolmogorov20] and Arnold [Reference Arnold1] focused on real analytic Hamiltonian systems. In contrast, Moser [Reference Moser25] illustrated that Hamiltonian systems do not necessarily need to be analytic; a high, albeit finite, level of regularity for the Hamiltonian suffices. This regularity requirement was later reduced to C 5 in work by [Reference Rüssmann and Kleine Nenner33]. Further important contributions on this topic can be found in [Reference Bounemoura4, Reference Herman19, Reference Koudjinan21, Reference Salamon35]. Moreover, the scenario where the frequency mapping has Lipschitz continuous parameters has been explored in [Reference Pöschel29]. A subsequent question of interest is: what are the implications when the regularity of the frequency mapping is merely Hölder continuous with respect to its parameters?
More precisely, we consider a family of Hamiltonian systems under small perturbations:
where ![]() $(y,x)\in G\times\mathbb{T}^n$ and ξ is a parameter in a bounded closed region
$(y,x)\in G\times\mathbb{T}^n$ and ξ is a parameter in a bounded closed region ![]() $O\subset \mathbb{R}^n$. The function
$O\subset \mathbb{R}^n$. The function ![]() $\omega(\cdot)$,
$\omega(\cdot)$, ![]() $\bar h(y,\cdot)=O(|y|^2)$ and
$\bar h(y,\cdot)=O(|y|^2)$ and ![]() $P(y,x,\cdot,\varepsilon)$ are Hölder continuous with respect to the parameter ξ with Hölder index β, for some
$P(y,x,\cdot,\varepsilon)$ are Hölder continuous with respect to the parameter ξ with Hölder index β, for some ![]() $0 \lt \beta \lt 1$. The function
$0 \lt \beta \lt 1$. The function ![]() $\bar h(\cdot,\xi)$ and
$\bar h(\cdot,\xi)$ and ![]() $P(\cdot,\cdot,\xi,\varepsilon)$ are real analytic with respect to y and x. Additionally, ɛ > 0 is a small parameter.
$P(\cdot,\cdot,\xi,\varepsilon)$ are real analytic with respect to y and x. Additionally, ɛ > 0 is a small parameter.
It is important to note that in the conventional KAM iteration process, the regularity of the frequency mapping concerning the parameters must be at least Lipschitz continuous. This ensures that the parameter domain remains intact. However, when the regularity of the frequency mapping is less stringent than Lipschitz continuous, the traditional method of parameter excavation becomes infeasible. This necessitates the exploration of novel approaches to address the issue.
1.3. Our work
Regarding regularity, when the frequency mapping is Hölder continuous with respect to parameters, we prove that the perturbed invariant tori retain the same Diophantine frequency as their unperturbed counterparts for Hamiltonian systems as described in (1.2), see theorem 2.1. For the degeneracy problem, persistence results under the highly degenerate Hamiltonian system (1.1) are proved in theorem 2.5.
We establish sufficient conditions based on the topological degree condition ![]() $\mathrm{(A0)}$ and the weak convexity condition
$\mathrm{(A0)}$ and the weak convexity condition ![]() $\mathrm{(A1)}$ for frequency mapping. Detailed descriptions of these conditions are provided in section 2. In deriving our primary results, we employ the quasi-linear KAM iteration procedure as in [Reference Chow, Li and Yi10, Reference Han, Li and Yi17, Reference Li and Yi23, Reference Qian, Li and Yang31]. Notably, we use the technique of translation parameters to counteract frequency drift. Specifically, we adjust the action variable to maintain constant frequency for the highly degenerate Hamiltonian system (1.1). It is also noteworthy that the weak convexity condition proposed in this paper is necessary regardless of the smoothness level of the frequency mapping, as evidenced by proposition 2.3.
$\mathrm{(A1)}$ for frequency mapping. Detailed descriptions of these conditions are provided in section 2. In deriving our primary results, we employ the quasi-linear KAM iteration procedure as in [Reference Chow, Li and Yi10, Reference Han, Li and Yi17, Reference Li and Yi23, Reference Qian, Li and Yang31]. Notably, we use the technique of translation parameters to counteract frequency drift. Specifically, we adjust the action variable to maintain constant frequency for the highly degenerate Hamiltonian system (1.1). It is also noteworthy that the weak convexity condition proposed in this paper is necessary regardless of the smoothness level of the frequency mapping, as evidenced by proposition 2.3.
It should be pointed out that the KAM-type theorems associated with parameter family are due to Moser [Reference Moser26], Pöschel [Reference Pöschel28]. However, our results are different from theirs: a Diophantine frequency can be given in advance, but Moser’s systems need to be modified in KAM iteration and hence cannot be given beforehand; in Pöschel’s approach, the frequency set need to be dug out in KAM process. Our method is to find a parameter in the family of systems by translating parameter. Of course, it does not work generally. Recently, the persistence of invariant tori with prescribed frequencies has been developed in [Reference Xu and Lu39, Reference Xu and You41]. Here we prove the persistence of invariant tori, which form a Hölder continuous family with respect to parameters. As showed by proposition 2.3, the weak convexity condition (A1) is sharp to such persistence.
The rest of this paper is organized as follows. In section 2, we state our main results (theorems 2.1, 2.5, 2.6 and 2.8). We describe the quasi-linear iterative scheme, show the detailed construction and estimates for one cycle of KAM steps in section 3. In section 4, we complete the proof of theorem 2.1 by deriving an iteration lemma and showing the convergence of KAM iterations. In section 5, we prove theorem 2.5 , which covers the analytic situation, and is also a special case of theorem 2.1. We also prove theorem 2.8 by directly computing. Finally, the proof of theorem 2.6 can be found in appendix B.
2. Main results
To state our main results, we first need to introduce a few definitions and notations.
(1) Given a domain
 $D\subset G\times \mathbb{T}^n$, we let
$D\subset G\times \mathbb{T}^n$, we let  $\bar{D}$,
$\bar{D}$,  $\partial D$ denote the closure and the boundary of D, respectively.
$\partial D$ denote the closure and the boundary of D, respectively.  $D^o:=\bar{D}\setminus\partial D$ refers to the interior.
$D^o:=\bar{D}\setminus\partial D$ refers to the interior.(2) We shall use the same symbol
 $\vert\cdot\vert$ to denote an equivalent vector norm and its induced matrix norm, absolute value of functions, etc, and use
$\vert\cdot\vert$ to denote an equivalent vector norm and its induced matrix norm, absolute value of functions, etc, and use  $\vert\cdot\vert_D$ to denote the supremum norm of functions on a domain D.
$\vert\cdot\vert_D$ to denote the supremum norm of functions on a domain D.(3) For the perturbation function
 $P(y,x,\xi)$, which is analytic about y and x and Hölder continuous about ξ with Hölder index β,
$P(y,x,\xi)$, which is analytic about y and x and Hölder continuous about ξ with Hölder index β,  $0 \lt \beta \lt 1$, we define its norm as follows
$0 \lt \beta \lt 1$, we define its norm as follows
 \begin{equation*}\vert\|P\|\vert_{D}={|P|_{D}}+\|P\|_{C^\beta}\end{equation*}
\begin{equation*}\vert\|P\|\vert_{D}={|P|_{D}}+\|P\|_{C^\beta}\end{equation*}where
(2.1) \begin{equation}\|P\|_{C^\beta}=\sup_{\xi\neq\zeta,~\xi,\zeta\in {O}}\frac{\vert P(y,x,\xi)-P(y,x,\zeta)\vert}{\vert\xi-\zeta\vert^\beta},~~~\forall (y,x)\in {D}.\end{equation}
\begin{equation}\|P\|_{C^\beta}=\sup_{\xi\neq\zeta,~\xi,\zeta\in {O}}\frac{\vert P(y,x,\xi)-P(y,x,\zeta)\vert}{\vert\xi-\zeta\vert^\beta},~~~\forall (y,x)\in {D}.\end{equation}(4) For any two complex column vectors ξ, η in the same space,
 $\langle\xi,\eta\rangle$ always stands for
$\langle\xi,\eta\rangle$ always stands for  $\xi^\top\eta$.
$\xi^\top\eta$.(5) id is the unit map, and Id is the unit matrix.
(6) For a vector-value function f, Df denotes the Jacobian matrix of f, and
 $J_f=det Df$ its Jacobian determinant.
$J_f=det Df$ its Jacobian determinant.(7) All Hamiltonians in the sequel are endowed with the standard symplectic structure.
(8) As pointed out in [Reference Pöschel30], the real analyticity of the Hamiltonian
 $H(y,x)$ about y and x on
$H(y,x)$ about y and x on  $G\times{\mathbb{T}^n}$ implies that the analyticity extends to a complex neighbourhood
$G\times{\mathbb{T}^n}$ implies that the analyticity extends to a complex neighbourhood  $D(s,r)$ of
$D(s,r)$ of  $G\times{\mathbb{T}^n}$, where
$G\times{\mathbb{T}^n}$, where  $D(s,r)$ is defined for some
$D(s,r)$ is defined for some  $0 \lt s,r \lt 1$, with
$0 \lt s,r \lt 1$, with \begin{equation*}D(s,r):=\{(y,x):|y| \lt s,\vert\textrm{Im}x\vert \lt r\}.\end{equation*}
\begin{equation*}D(s,r):=\{(y,x):|y| \lt s,\vert\textrm{Im}x\vert \lt r\}.\end{equation*}(9) For
 $\forall \delta \gt 0$,
$\forall \delta \gt 0$,  $y_0\in G$, let
$y_0\in G$, let \begin{align*}
B_\delta(y_0)&=:\{y\in G:\vert y-y_0\vert \lt \delta\},\\
\bar B_\delta(y_0)&=:\{y\in G:\vert y-y_0\vert\leq\delta\}.
\end{align*}
\begin{align*}
B_\delta(y_0)&=:\{y\in G:\vert y-y_0\vert \lt \delta\},\\
\bar B_\delta(y_0)&=:\{y\in G:\vert y-y_0\vert\leq\delta\}.
\end{align*}
We are now ready to state our assumptions. Mainly we consider (1.2), i.e., for any ɛ > 0 small enough, we consider the parameterized family of perturbed Hamiltonian systems
 \begin{equation*}
\left\{
\begin{array}{ll}
H:G\times \mathbb{T}^n\times O\rightarrow \mathbb{R}^1,\\
H(y,x,\xi)=\langle\omega(\xi),y\rangle{+\bar h(y,\xi)}+\varepsilon P(y,x,\xi,\varepsilon).
\end{array}
\right.
\end{equation*}
\begin{equation*}
\left\{
\begin{array}{ll}
H:G\times \mathbb{T}^n\times O\rightarrow \mathbb{R}^1,\\
H(y,x,\xi)=\langle\omega(\xi),y\rangle{+\bar h(y,\xi)}+\varepsilon P(y,x,\xi,\varepsilon).
\end{array}
\right.
\end{equation*}First, we make the following assumptions:
(A0) Fix
 $\xi_0\in O^o$ such that
(2.2)
$\xi_0\in O^o$ such that
(2.2) \begin{align}
&\deg\left(\omega(\cdot), O^o, \omega(\xi_0)\right)\neq0.
\end{align}
\begin{align}
&\deg\left(\omega(\cdot), O^o, \omega(\xi_0)\right)\neq0.
\end{align}(A1) There exists a small neighbourhood
 $B_\varsigma(\xi_0)\subset O^o$ with ς > 0 and a constant σ > 0 such that(2.3)
$B_\varsigma(\xi_0)\subset O^o$ with ς > 0 and a constant σ > 0 such that(2.3) \begin{align}
\left\vert\omega(\xi)-\omega(\xi_{*})\right\vert\geq \sigma\left\vert\xi-\xi_{*}\right\vert^\beta,~~~~\forall \xi,\xi_{*}\in B_\varsigma(\xi_0),
\end{align}
\begin{align}
\left\vert\omega(\xi)-\omega(\xi_{*})\right\vert\geq \sigma\left\vert\xi-\xi_{*}\right\vert^\beta,~~~~\forall \xi,\xi_{*}\in B_\varsigma(\xi_0),
\end{align}where β is defined in (2.1).
(A2) For the given
 $\xi_0\in O^o$,
$\xi_0\in O^o$,  $\omega(\xi_0)$ satisfies the Diophantine condition(2.4)
$\omega(\xi_0)$ satisfies the Diophantine condition(2.4) \begin{align}
\left\vert\langle k,\omega(\xi_0)\rangle\right\vert \gt \frac{\gamma}{\vert k\vert^\tau},~~~k\in{\mathbb{Z}^n\setminus{\{0\}}},
\end{align}
\begin{align}
\left\vert\langle k,\omega(\xi_0)\rangle\right\vert \gt \frac{\gamma}{\vert k\vert^\tau},~~~k\in{\mathbb{Z}^n\setminus{\{0\}}},
\end{align}where
 $k=(k_1,\cdots,k_n)$,
$k=(k_1,\cdots,k_n)$,  $\vert k\vert=\left\vert k_1\right\vert+\cdots+\left\vert k_n\right\vert$, γ > 0 and
$\vert k\vert=\left\vert k_1\right\vert+\cdots+\left\vert k_n\right\vert$, γ > 0 and  $\tau \gt n-1$.
$\tau \gt n-1$.
Then, we have the following main results:
Theorem 2.1 Consider Hamiltonian system (1.2). Assume that ![]() $\mathrm{(A0)}$,
$\mathrm{(A0)}$, ![]() $\mathrm{(A1)}$ and
$\mathrm{(A1)}$ and ![]() $\mathrm{(A2)}$ hold. Then there exists a sufficiently small
$\mathrm{(A2)}$ hold. Then there exists a sufficiently small ![]() $\varepsilon_0 \gt 0$, for any
$\varepsilon_0 \gt 0$, for any ![]() $0 \lt \varepsilon \lt \varepsilon_0$, there exist
$0 \lt \varepsilon \lt \varepsilon_0$, there exist ![]() $\xi_\varepsilon\in O$ with
$\xi_\varepsilon\in O$ with ![]() $\xi_\varepsilon\rightarrow\xi_0$ as
$\xi_\varepsilon\rightarrow\xi_0$ as ![]() $\varepsilon\rightarrow0$ and a symplectic transformation
$\varepsilon\rightarrow0$ and a symplectic transformation ![]() $\Psi_*$ such that
$\Psi_*$ such that
where ![]() $e_*$ is a constant,
$e_*$ is a constant, ![]() $\bar h_*(y,\xi_{\varepsilon})=O(\vert y\vert^2)$,
$\bar h_*(y,\xi_{\varepsilon})=O(\vert y\vert^2)$, ![]() $P_*=O(\vert y\vert^2)$. Thus the perturbed Hamiltonian system
$P_*=O(\vert y\vert^2)$. Thus the perturbed Hamiltonian system ![]() $H(y,x,\xi_\varepsilon,\varepsilon)$ admits an invariant torus with frequency
$H(y,x,\xi_\varepsilon,\varepsilon)$ admits an invariant torus with frequency ![]() $\omega(\xi_0)$.
$\omega(\xi_0)$.
Moreover, there is a Hölder continuous family of  $\xi_\varepsilon(\hat\xi_0)$ with respect to
$\xi_\varepsilon(\hat\xi_0)$ with respect to ![]() $\hat\xi_0\in \hat O$, where
$\hat\xi_0\in \hat O$, where
 \begin{align*}\hat O & =\left\{\hat\xi_0\in O:|\omega(\hat \xi_0)-\omega(\xi_0)| \lt d,|\langle k,\omega(\hat\xi_0)\rangle| \gt \frac{\gamma}{|k|^\tau},k\in\mathbb{Z}^n\backslash\{0\}\right\},\nonumber\\ d & =\min_{\xi\in\partial O}\left\{\;|\omega(\xi)-\omega(\xi_0)|\;\right\},\end{align*}
\begin{align*}\hat O & =\left\{\hat\xi_0\in O:|\omega(\hat \xi_0)-\omega(\xi_0)| \lt d,|\langle k,\omega(\hat\xi_0)\rangle| \gt \frac{\gamma}{|k|^\tau},k\in\mathbb{Z}^n\backslash\{0\}\right\},\nonumber\\ d & =\min_{\xi\in\partial O}\left\{\;|\omega(\xi)-\omega(\xi_0)|\;\right\},\end{align*} such that the perturbed Hamiltonian system  $H(y,x,\xi_\varepsilon(\hat\xi_0),\varepsilon)$ admits an invariant torus with frequency
$H(y,x,\xi_\varepsilon(\hat\xi_0),\varepsilon)$ admits an invariant torus with frequency  $\omega(\hat\xi_0)$, and
$\omega(\hat\xi_0)$, and  $\xi_\varepsilon(\hat\xi_0)\rightarrow\hat\xi_0$ as
$\xi_\varepsilon(\hat\xi_0)\rightarrow\hat\xi_0$ as ![]() $\varepsilon\rightarrow0$.
$\varepsilon\rightarrow0$.
Remark 2.2. It should be emphasized that we deal with the degenerate Hamiltonian system in which the frequency mapping and the perturbation are Hölder continuous about parameters in this theorem.
In the following, we will give some examples to state that conditions ![]() $\mathrm{(A0)}$ and
$\mathrm{(A0)}$ and ![]() $\mathrm{(A1)}$ are indispensable, especially for condition
$\mathrm{(A1)}$ are indispensable, especially for condition ![]() $\mathrm{(A1)}$. See below for a counter example:
$\mathrm{(A1)}$. See below for a counter example:
Proposition 2.3. Consider Hamiltonian system (1.2), for n = 2, with
 \begin{equation*}\omega(\xi)=(\omega_1(\xi_1),\omega_2(\xi_2))^\top,~~~\bar h(y,\xi)=0~~~\varepsilon P=P_0(\varepsilon)y_2,\end{equation*}
\begin{equation*}\omega(\xi)=(\omega_1(\xi_1),\omega_2(\xi_2))^\top,~~~\bar h(y,\xi)=0~~~\varepsilon P=P_0(\varepsilon)y_2,\end{equation*} where ![]() $\xi=(\xi_1,\xi_2)$,
$\xi=(\xi_1,\xi_2)$,
 \begin{align*}
&\omega_1(\xi_1)=\bar{\omega}_1+\xi_1,~~\xi_1\in(-1,1),\\
&\omega_2{(\xi_2)}=\left\{\begin{array}{lll}
\bar{\omega}_2+\exp\{-\frac{1}{(\xi_2+{\frac{1}{2}})^2}\},~~~&\xi_2\in(-1,-\frac{1}{2}),\\
\bar{\omega}_2,~~~&\xi_2\in[-\frac{1}{2},\frac{1}{2}],\\
\bar{\omega}_2-\exp\{-\frac{1}{(\xi_2-{\frac{1}{2}})^2}\},~~~&\xi_2\in(\frac{1}{2},1),
\end{array}\right.
\end{align*}
\begin{align*}
&\omega_1(\xi_1)=\bar{\omega}_1+\xi_1,~~\xi_1\in(-1,1),\\
&\omega_2{(\xi_2)}=\left\{\begin{array}{lll}
\bar{\omega}_2+\exp\{-\frac{1}{(\xi_2+{\frac{1}{2}})^2}\},~~~&\xi_2\in(-1,-\frac{1}{2}),\\
\bar{\omega}_2,~~~&\xi_2\in[-\frac{1}{2},\frac{1}{2}],\\
\bar{\omega}_2-\exp\{-\frac{1}{(\xi_2-{\frac{1}{2}})^2}\},~~~&\xi_2\in(\frac{1}{2},1),
\end{array}\right.
\end{align*} ![]() $\bar{\omega}(\xi_0)=(\bar{\omega}_1,\bar{\omega}_2)^\top$ satisfies Diophantine condition (2.4), and
$\bar{\omega}(\xi_0)=(\bar{\omega}_1,\bar{\omega}_2)^\top$ satisfies Diophantine condition (2.4), and
 \begin{equation*}P_0(\varepsilon)=\left\{\begin{array}{lll}
0,&&\varepsilon=0, \\
\varepsilon^\ell\sin\frac{1}{\varepsilon},&&\varepsilon\neq0,\,\ell\in \mathbb{Z}^+\setminus\{0\}.
\end{array}\right.\end{equation*}
\begin{equation*}P_0(\varepsilon)=\left\{\begin{array}{lll}
0,&&\varepsilon=0, \\
\varepsilon^\ell\sin\frac{1}{\varepsilon},&&\varepsilon\neq0,\,\ell\in \mathbb{Z}^+\setminus\{0\}.
\end{array}\right.\end{equation*} Then condition ![]() $\mathrm{(A1)}$ fails for any parameter
$\mathrm{(A1)}$ fails for any parameter  $\xi\in(-\frac{1}{2},\frac{1}{2})\times(-\frac{1}{2},\frac{1}{2})$. Moreover, although the topological degree is not equal to 0, we cannot find ξɛ such that
$\xi\in(-\frac{1}{2},\frac{1}{2})\times(-\frac{1}{2},\frac{1}{2})$. Moreover, although the topological degree is not equal to 0, we cannot find ξɛ such that ![]() $\xi_\varepsilon\rightarrow\xi_0$ as
$\xi_\varepsilon\rightarrow\xi_0$ as ![]() $\varepsilon\rightarrow0$.
$\varepsilon\rightarrow0$.
See appendix A for the complete proof.
Remark 2.4. This counter example implies that ![]() $\mathrm{(A1)}$ is necessary to ensure
$\mathrm{(A1)}$ is necessary to ensure ![]() $\xi_\varepsilon\rightarrow\xi_0$, as
$\xi_\varepsilon\rightarrow\xi_0$, as ![]() $\varepsilon\rightarrow0$.
$\varepsilon\rightarrow0$.
Nevertheless, one asks what happens to the frequency mapping in the analytic situation. As a special case of our theorem 2.1, we also obtain the Kolmogorov’s theorem for analytic Hamiltonian systems with degeneracy. This is stated in the following theorem.
Theorem 2.5 Consider real analytic Hamiltonian system (1.1). Fix ![]() $\xi_0\in G$ such that
$\xi_0\in G$ such that ![]() $\mathrm{(A0)}$,
$\mathrm{(A0)}$, ![]() $\mathrm{(A1)}$ and
$\mathrm{(A1)}$ and ![]() $\mathrm{(A2)}$ hold for
$\mathrm{(A2)}$ hold for ![]() $\omega(\xi)=\nabla h(\xi)$, O = G, and
$\omega(\xi)=\nabla h(\xi)$, O = G, and ![]() $\beta\geq 1$. Then there exists a sufficiently small positive constant
$\beta\geq 1$. Then there exists a sufficiently small positive constant ![]() $\varepsilon' \gt 0$ such that if
$\varepsilon' \gt 0$ such that if ![]() $0 \lt \varepsilon \lt \varepsilon'$, there exists
$0 \lt \varepsilon \lt \varepsilon'$, there exists ![]() $y_\varepsilon\in G$ such that Hamiltonian system (1.1) at
$y_\varepsilon\in G$ such that Hamiltonian system (1.1) at ![]() $y=y_\varepsilon$ admits an invariant torus with frequency
$y=y_\varepsilon$ admits an invariant torus with frequency ![]() $\nabla h(\xi_0)$.
$\nabla h(\xi_0)$.
This theorem is proved in section 5.1.
Next, we give an example that satisfies conditions ![]() $\mathrm{(A0)}$-
$\mathrm{(A0)}$-![]() $\mathrm{(A1)}$. For simplicity we use the action variable y as the parameter ξ.
$\mathrm{(A1)}$. For simplicity we use the action variable y as the parameter ξ.
Theorem 2.6 Consider Hamiltonian system (1.1) with
 \begin{equation*}
h(y)=\langle \omega,y\rangle+\frac{1}{2l+2}\vert y\vert^{2l+2},
\end{equation*}
\begin{equation*}
h(y)=\langle \omega,y\rangle+\frac{1}{2l+2}\vert y\vert^{2l+2},
\end{equation*} where ![]() $y\in G\subset \mathbb{R}^n$, l is a positive integer,
$y\in G\subset \mathbb{R}^n$, l is a positive integer, ![]() $\omega\in \mathbb{R}^n\setminus{\{0\}}$ satisfies the Diophantine condition (2.4). Then Hamiltonian system (1.1) admits an invariant torus with frequency ω for any small enough perturbation.
$\omega\in \mathbb{R}^n\setminus{\{0\}}$ satisfies the Diophantine condition (2.4). Then Hamiltonian system (1.1) admits an invariant torus with frequency ω for any small enough perturbation.
The proof can be found in appendix B.
Proposition 2.7. If  $h(y)=\langle \omega,y\rangle+\frac{1}{2l+1}\left\vert y\right\vert^{2l+1}$ in Hamiltonian system (1.1),
$h(y)=\langle \omega,y\rangle+\frac{1}{2l+1}\left\vert y\right\vert^{2l+1}$ in Hamiltonian system (1.1), ![]() $\omega\in \mathbb{R}^n\setminus{\{0\}}$ satisfies the Diophantine condition (2.4), then the system may not admit invariant torus with frequency ω.
$\omega\in \mathbb{R}^n\setminus{\{0\}}$ satisfies the Diophantine condition (2.4), then the system may not admit invariant torus with frequency ω.
The proof can be found in appendix C.
Above results imply that condition ![]() $\mathrm{(A0)}$ is indispensable for n > 1 case. Furthermore, we also prove that for n = 1, the persistence results in theorem 2.6 hold under some weaker conditions, provided that the frequency satisfies Diophantine condition
$\mathrm{(A0)}$ is indispensable for n > 1 case. Furthermore, we also prove that for n = 1, the persistence results in theorem 2.6 hold under some weaker conditions, provided that the frequency satisfies Diophantine condition ![]() $\mathrm{(A2)}$.
$\mathrm{(A2)}$.
Theorem 2.8 Consider Hamiltonian (1.1), for n = 1, with
where ![]() $y\in G=[-1,1]\subset \mathbb{R}^1$, ω satisfies Diophantine condition (2.4).
$y\in G=[-1,1]\subset \mathbb{R}^1$, ω satisfies Diophantine condition (2.4).
(1) If
 $g(y)\in C^{2\ell+1}$,
$g(y)\in C^{2\ell+1}$,  $g'(0)=\cdots=g^{2\ell}(0)=0$,
$g'(0)=\cdots=g^{2\ell}(0)=0$,  $g^{2\ell+1}(0)\neq 0$,
$g^{2\ell+1}(0)\neq 0$,  $\ell$ is a positive integer, then the perturbed system admits at least two invariant tori with frequency ω for the small enough perturbation satisfying
$\ell$ is a positive integer, then the perturbed system admits at least two invariant tori with frequency ω for the small enough perturbation satisfying  $\varepsilon P'(y)\, sign (g^{2\ell+1}(0)) \lt 0$; conversely, if
$\varepsilon P'(y)\, sign (g^{2\ell+1}(0)) \lt 0$; conversely, if  $\varepsilon P'(y)\, sign (g^{2\ell+1}(0)) \gt 0$, the unperturbed invariant torus with frequency ω will be destroyed.
$\varepsilon P'(y)\, sign (g^{2\ell+1}(0)) \gt 0$, the unperturbed invariant torus with frequency ω will be destroyed.(2) If
 $g(y)\in C^{2\ell+2}$,
$g(y)\in C^{2\ell+2}$,  $g'(0)=\cdots=g^{2\ell+1}(0)=0$,
$g'(0)=\cdots=g^{2\ell+1}(0)=0$,  $g^{2\ell+2}(0)\neq 0$,
$g^{2\ell+2}(0)\neq 0$,  $\ell$ is a positive integer, then the perturbed system admits an invariant tori with frequency ω for any small enough perturbation.
$\ell$ is a positive integer, then the perturbed system admits an invariant tori with frequency ω for any small enough perturbation.
Remark 2.9. We do not know whether the results in theorem 2.8 can be extended to higher dimensions or not.
3. KAM step
In this section, we describe the quasi-linear iterative scheme, show the detailed construction and estimates for one cycle of KAM steps, which is essential to study the KAM theory, see [Reference Chow, Li and Yi10, Reference Han, Li and Yi17, Reference Li and Yi22, Reference Li and Yi23, Reference Pöschel30]. It should be pointed out that in our KAM iteration, we translate the parameter domain; while in the usual KAM iteration, one has to dig out a decreasing series of parameter domains, see [Reference Chow, Li and Yi10, Reference Han, Li and Yi17, Reference Li and Yi23, Reference Pöschel29–Reference Qian, Li and Yang32].
3.1. Description of the 0th KAM step
Given an integer ![]() $m\geq\beta+1$, where β is defined in (2.1). Denote
$m\geq\beta+1$, where β is defined in (2.1). Denote  $\rho=\frac{1}{2(m+1)}$, and let η > 0 be an integer such that
$\rho=\frac{1}{2(m+1)}$, and let η > 0 be an integer such that ![]() $(1+\rho)^\eta \gt 2$. We define
$(1+\rho)^\eta \gt 2$. We define
 \begin{equation}\gamma=\varepsilon^{\frac{1}{4(n+m+2)}}.\end{equation}
\begin{equation}\gamma=\varepsilon^{\frac{1}{4(n+m+2)}}.\end{equation}Consider Hamiltonian (1.2). We first define the following 0th KAM step parameters:
 \begin{align}
&r_0=r,~~~~~\gamma_0=\gamma,~~~~~e_0=0,
~~~~~{\bar{h}_0=\bar h(y,\xi)},~~~~~\omega_0(\xi)=\omega(\xi),\notag\\ & \mu_0=\varepsilon^{\frac{1}{8\eta(\tau+1)(m+1)}},\\
&s_0=\frac{s\gamma_0}{16(M^*+2)K_1^{\tau+1}},~~~~{O_0=\left\{\xi:\xi\in B_{\varrho_0}(\xi_0),~\varrho_0= s_0^{\frac{1}{\beta}}\right\},}\notag\\
&D(s_0,r_0):=\left\{(y,x):|y| \lt s_0,\vert\textrm{Im}x\vert \lt r_0\right\},\notag
\end{align}
\begin{align}
&r_0=r,~~~~~\gamma_0=\gamma,~~~~~e_0=0,
~~~~~{\bar{h}_0=\bar h(y,\xi)},~~~~~\omega_0(\xi)=\omega(\xi),\notag\\ & \mu_0=\varepsilon^{\frac{1}{8\eta(\tau+1)(m+1)}},\\
&s_0=\frac{s\gamma_0}{16(M^*+2)K_1^{\tau+1}},~~~~{O_0=\left\{\xi:\xi\in B_{\varrho_0}(\xi_0),~\varrho_0= s_0^{\frac{1}{\beta}}\right\},}\notag\\
&D(s_0,r_0):=\left\{(y,x):|y| \lt s_0,\vert\textrm{Im}x\vert \lt r_0\right\},\notag
\end{align} where ![]() $0 \lt s_0,\gamma_0,\mu_0\leq 1$,
$0 \lt s_0,\gamma_0,\mu_0\leq 1$, ![]() $\tau \gt n-1$,
$\tau \gt n-1$, ![]() $M^* \gt 0$ is a constant defined as in lemma 3.4, and
$M^* \gt 0$ is a constant defined as in lemma 3.4, and
 \begin{align*}
K_1=\left(\left[\log\frac{1}{\mu_0}\right]+1\right)^{3\eta}.
\end{align*}
\begin{align*}
K_1=\left(\left[\log\frac{1}{\mu_0}\right]+1\right)^{3\eta}.
\end{align*}Therefore, we can write
 \begin{align*}
H_0&=: H(y,x,\xi,\varepsilon)=N_0+P_0,\\
N_0&=: N_0(y,\xi)=e_0+\langle\omega_0(\xi),y\rangle+\bar{h}_0,\\
P_0&=:\varepsilon P(y,x,\xi,\varepsilon),
\end{align*}
\begin{align*}
H_0&=: H(y,x,\xi,\varepsilon)=N_0+P_0,\\
N_0&=: N_0(y,\xi)=e_0+\langle\omega_0(\xi),y\rangle+\bar{h}_0,\\
P_0&=:\varepsilon P(y,x,\xi,\varepsilon),
\end{align*} where ![]() $(y,x,\xi)\in D(s_0,r_0)\times O_0$.
$(y,x,\xi)\in D(s_0,r_0)\times O_0$.
We first prove an important estimate.
 \begin{equation}
\vert\|P_0\|\vert_{D(s_0,r_0)}\leq\gamma_0^{n+m+2}s_0^m\mu_0.
\end{equation}
\begin{equation}
\vert\|P_0\|\vert_{D(s_0,r_0)}\leq\gamma_0^{n+m+2}s_0^m\mu_0.
\end{equation}Proof. Using the fact  $\gamma_0^{n+m+2}=\varepsilon^{\frac{1}{4}}$ and
$\gamma_0^{n+m+2}=\varepsilon^{\frac{1}{4}}$ and  $\left[\log\frac{1}{\mu_0}\right]+1 \lt \frac{1}{\mu_0}$, we have
$\left[\log\frac{1}{\mu_0}\right]+1 \lt \frac{1}{\mu_0}$, we have
 \begin{align*}
s_0^m=\frac{s^m\varepsilon^{\frac{m}{4(n+m+2)}}}{16^m(M^*+2)^mK_1^{m(\tau+1)}} \gt \frac{s^m\varepsilon^{\frac{m}{4(n+m+2)}}\mu_0^{3\eta m(\tau+1)}}{16^m(M^*+2)^m}\geq\frac{s^m\varepsilon^{\frac{m}{4(n+m+2)}+\frac{3}{8}}}{16^m(M^*+2)^m}.
\end{align*}
\begin{align*}
s_0^m=\frac{s^m\varepsilon^{\frac{m}{4(n+m+2)}}}{16^m(M^*+2)^mK_1^{m(\tau+1)}} \gt \frac{s^m\varepsilon^{\frac{m}{4(n+m+2)}}\mu_0^{3\eta m(\tau+1)}}{16^m(M^*+2)^m}\geq\frac{s^m\varepsilon^{\frac{m}{4(n+m+2)}+\frac{3}{8}}}{16^m(M^*+2)^m}.
\end{align*} Moreover, let ![]() $\varepsilon_0 \gt 0$ be small enough so that
$\varepsilon_0 \gt 0$ be small enough so that
 \begin{equation}
\varepsilon_0^{\frac{1}{8}-\frac{1}{8\eta(\tau+1)(m+1)}}\vert\|P\|\vert_{D(s_0,r_0)}\frac{16^m(M^*+2)^m}{s^m}\leq 1,
\end{equation}
\begin{equation}
\varepsilon_0^{\frac{1}{8}-\frac{1}{8\eta(\tau+1)(m+1)}}\vert\|P\|\vert_{D(s_0,r_0)}\frac{16^m(M^*+2)^m}{s^m}\leq 1,
\end{equation} using the fact that  $\mu_0=\varepsilon^{\frac{1}{8\eta(\tau+1)(m+1)}}$, we get
$\mu_0=\varepsilon^{\frac{1}{8\eta(\tau+1)(m+1)}}$, we get
 \begin{align}
\gamma_0^{n+m+2}s_0^m\mu_0&\geq\frac{s^m\varepsilon^{\frac{m}{4(n+m+2)}+\frac{3}{8}+\frac{1}{4}+\frac{1}{8\eta(\tau+1)(m+1)}}}{16^m(M^*+2)^m}
\geq\frac{s^m\varepsilon^{\frac{1}{4}+\frac{3}{8}+\frac{1}{4}+\frac{1}{8\eta(\tau+1)(m+1)}}}{16^m(M^*+2)^m}
\notag\\ &=\varepsilon^{\frac{7}{8}}\frac{s^m\varepsilon^{\frac{1}{8\eta(\tau+1)(m+1)}}}{16^m(M^*+2)^m},
\end{align}
\begin{align}
\gamma_0^{n+m+2}s_0^m\mu_0&\geq\frac{s^m\varepsilon^{\frac{m}{4(n+m+2)}+\frac{3}{8}+\frac{1}{4}+\frac{1}{8\eta(\tau+1)(m+1)}}}{16^m(M^*+2)^m}
\geq\frac{s^m\varepsilon^{\frac{1}{4}+\frac{3}{8}+\frac{1}{4}+\frac{1}{8\eta(\tau+1)(m+1)}}}{16^m(M^*+2)^m}
\notag\\ &=\varepsilon^{\frac{7}{8}}\frac{s^m\varepsilon^{\frac{1}{8\eta(\tau+1)(m+1)}}}{16^m(M^*+2)^m},
\end{align} and by (3.4) and ![]() $0 \lt \varepsilon \lt \varepsilon_0$,
$0 \lt \varepsilon \lt \varepsilon_0$,
 \begin{align*}
\varepsilon^{\frac{1}{8}-\frac{1}{8\eta(\tau+1)(m+1)}}\vert\|P\|\vert_{D(s_0,r_0)}\frac{16^m(M^*+2)^m}{s^m}\leq 1,
\end{align*}
\begin{align*}
\varepsilon^{\frac{1}{8}-\frac{1}{8\eta(\tau+1)(m+1)}}\vert\|P\|\vert_{D(s_0,r_0)}\frac{16^m(M^*+2)^m}{s^m}\leq 1,
\end{align*}i.e.,
 \begin{align}
\varepsilon^{\frac{1}{8}}\vert\|P\|\vert_{D(s_0,r_0)}\leq \frac{s^m\varepsilon^{\frac{1}{8\eta(\tau+1)(m+1)}}}{16^m(M^*+2)^m}.
\end{align}
\begin{align}
\varepsilon^{\frac{1}{8}}\vert\|P\|\vert_{D(s_0,r_0)}\leq \frac{s^m\varepsilon^{\frac{1}{8\eta(\tau+1)(m+1)}}}{16^m(M^*+2)^m}.
\end{align} \begin{align*}
\vert\|P_0\|\vert_{D(s_0,r_0)}=\varepsilon^{\frac{7}{8}} \varepsilon^{\frac{1}{8}}\vert\|P\|\vert_{D(s_0,r_0)}\leq \varepsilon^{\frac{7}{8}}\frac{s^m\varepsilon^{\frac{1}{8\eta(\tau+1)(m+1)}}}{16^m(M^*+2)^m}\leq\gamma_0^{n+m+2}s_0^m\mu_0,
\end{align*}
\begin{align*}
\vert\|P_0\|\vert_{D(s_0,r_0)}=\varepsilon^{\frac{7}{8}} \varepsilon^{\frac{1}{8}}\vert\|P\|\vert_{D(s_0,r_0)}\leq \varepsilon^{\frac{7}{8}}\frac{s^m\varepsilon^{\frac{1}{8\eta(\tau+1)(m+1)}}}{16^m(M^*+2)^m}\leq\gamma_0^{n+m+2}s_0^m\mu_0,
\end{align*}which implies (3.3).
This completes the proof.
3.2. Induction from the νth KAM step
3.2.1. Description of the νth KAM step
We now define the νth KAM step parameters:
 \begin{equation*}r_\nu=\frac{r_{\nu-1}}{2}+\frac{r_0}{4},~~~s_\nu=\frac{1}{8}\mu_{\nu-1}^{2\rho}s_{\nu-1},~~~\mu_\nu=8^m\mu_{\nu-1}^{1+\rho},\end{equation*}
\begin{equation*}r_\nu=\frac{r_{\nu-1}}{2}+\frac{r_0}{4},~~~s_\nu=\frac{1}{8}\mu_{\nu-1}^{2\rho}s_{\nu-1},~~~\mu_\nu=8^m\mu_{\nu-1}^{1+\rho},\end{equation*} where  $\rho=\frac{1}{2(m+1)}$.
$\rho=\frac{1}{2(m+1)}$.
Now, suppose that at νth step, we have arrived at the following Hamiltonian:
 \begin{equation}
\begin{aligned}
H_\nu&=N_\nu+P_\nu,~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\\
N_\nu&=e_\nu+\langle\omega_\nu(\xi),y\rangle+\bar{h}_\nu(y,\xi),
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
H_\nu&=N_\nu+P_\nu,~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\\
N_\nu&=e_\nu+\langle\omega_\nu(\xi),y\rangle+\bar{h}_\nu(y,\xi),
\end{aligned}
\end{equation} defined on ![]() $D(s_\nu,r_\nu)\times O_{\nu}$ and
$D(s_\nu,r_\nu)\times O_{\nu}$ and
 \begin{equation}
\left\vert\left\|P_\nu\right\|\right\vert_{D(s_\nu,r_\nu)}\leq\gamma_0^{n+m+2}s_\nu^m\mu_\nu.
\end{equation}
\begin{equation}
\left\vert\left\|P_\nu\right\|\right\vert_{D(s_\nu,r_\nu)}\leq\gamma_0^{n+m+2}s_\nu^m\mu_\nu.
\end{equation}The equation of motion associated to Hν is
 \begin{equation}
\left\{
\begin{array}{ll}
\dot{y}_\nu=-\partial_{x_\nu} H_\nu,\\
\dot{x}_\nu=~~\partial_{y_\nu} H_\nu.
\end{array}
\right.
\end{equation}
\begin{equation}
\left\{
\begin{array}{ll}
\dot{y}_\nu=-\partial_{x_\nu} H_\nu,\\
\dot{x}_\nu=~~\partial_{y_\nu} H_\nu.
\end{array}
\right.
\end{equation} Except for additional instructions,we will omit the index for all quantities of the present KAM step (at νth step) and use + to index all quantities (Hamiltonians, domains, normal forms, perturbations, transformations, etc.) in the next KAM step (at ![]() $(\nu+1)$th step). Using this notation, ξν is abbreviated as ξ, which can easily be confused with the parameter ξ. Therefore, we will not omit the subscript of ξν and continue to denote it as ξν. To simplify the notations, we will not specify the dependence of P,
$(\nu+1)$th step). Using this notation, ξν is abbreviated as ξ, which can easily be confused with the parameter ξ. Therefore, we will not omit the subscript of ξν and continue to denote it as ξν. To simplify the notations, we will not specify the dependence of P, ![]() $P_+$ etc. All the constants c 1-c 6 below are positive and independent of the iteration process, and we will also use c to denote any intermediate positive constant which is independent of the iteration process.
$P_+$ etc. All the constants c 1-c 6 below are positive and independent of the iteration process, and we will also use c to denote any intermediate positive constant which is independent of the iteration process.
Define
 \begin{align*}
r_+&=\frac{r}{2}+\frac{r_0}{4},\\
s_+&=\frac{1}{8}\alpha s,~~~~~\alpha=\mu^{2\rho}=\mu^{\frac{1}{m+1}},\\
\mu_+&=8^mc_0\mu^{1+\rho},~~~~~c_0=\max\{1,c_1,c_2,\cdots,c_6\},\\
K_+&=\left(\left[\log\frac{1}{\mu}\right]+1\right)^{3\eta},\\
\hat{D}&=D\left(s,r_++\frac{7}{8}(r-r_+)\right),\\
\tilde{D}&=D\left(\frac{1}{2} s,r_++\frac{6}{8}(r-r_+)\right),\\
D(s)&=\{y\in C^n:\vert y\vert \lt s\},\\
D_{\frac{i}{8}\alpha}&=D\left(\frac{i}{8}\alpha s,r_++\frac{i-1}{8}(r-r_+)\right), ~~i=1,2,\cdots,8,\\
D_+&=D_{\frac{1}{8}\alpha}=D(s_+,r_+),\\
O_+&=\left\{\xi:\xi\in B_{\varrho}(\xi_\nu),~\varrho= s^{\frac{1}{\beta}}\right\},\\
\Gamma(r-r_+)&=\sum_{0 \lt \vert k\vert\leq K_+}\left\vert k\right\vert^{6\tau+7}e^{-\vert k\vert\frac{r-r_+}{8}}.
\end{align*}
\begin{align*}
r_+&=\frac{r}{2}+\frac{r_0}{4},\\
s_+&=\frac{1}{8}\alpha s,~~~~~\alpha=\mu^{2\rho}=\mu^{\frac{1}{m+1}},\\
\mu_+&=8^mc_0\mu^{1+\rho},~~~~~c_0=\max\{1,c_1,c_2,\cdots,c_6\},\\
K_+&=\left(\left[\log\frac{1}{\mu}\right]+1\right)^{3\eta},\\
\hat{D}&=D\left(s,r_++\frac{7}{8}(r-r_+)\right),\\
\tilde{D}&=D\left(\frac{1}{2} s,r_++\frac{6}{8}(r-r_+)\right),\\
D(s)&=\{y\in C^n:\vert y\vert \lt s\},\\
D_{\frac{i}{8}\alpha}&=D\left(\frac{i}{8}\alpha s,r_++\frac{i-1}{8}(r-r_+)\right), ~~i=1,2,\cdots,8,\\
D_+&=D_{\frac{1}{8}\alpha}=D(s_+,r_+),\\
O_+&=\left\{\xi:\xi\in B_{\varrho}(\xi_\nu),~\varrho= s^{\frac{1}{\beta}}\right\},\\
\Gamma(r-r_+)&=\sum_{0 \lt \vert k\vert\leq K_+}\left\vert k\right\vert^{6\tau+7}e^{-\vert k\vert\frac{r-r_+}{8}}.
\end{align*}3.2.2. Construct a symplectic transformation
We will construct a symplectic coordinate transformation ![]() $\Phi_{+}$:
$\Phi_{+}$:
such that it transforms the Hamiltonian (![]() $3.7$) into the Hamiltonian of the next KAM cycle (at
$3.7$) into the Hamiltonian of the next KAM cycle (at ![]() $(\nu+1)$th step), i.e.,
$(\nu+1)$th step), i.e.,
where ![]() $N_{+}$ and
$N_{+}$ and ![]() $P_{+}$ have similar properties as N and P respectively on
$P_{+}$ have similar properties as N and P respectively on ![]() $D(s_{+},r_{+})\times O_+$, and the equation of motion (3.9) is changed into
$D(s_{+},r_{+})\times O_+$, and the equation of motion (3.9) is changed into
 \begin{equation}
\left\{
\begin{array}{ll}
\dot{y}_{+}=-\partial_{x_{+}} H_{+},\\
\dot{x}_{+}=~~\partial_{y_{+}} H_{+}.
\end{array}
\right.
\end{equation}
\begin{equation}
\left\{
\begin{array}{ll}
\dot{y}_{+}=-\partial_{x_{+}} H_{+},\\
\dot{x}_{+}=~~\partial_{y_{+}} H_{+}.
\end{array}
\right.
\end{equation} In the following, we prove (3.12). Let  $\Phi_+(y_+,x_+):=\left(\Phi_+^1(y_+,x_+),\Phi_+^2(y_+,x_+)\right)$, by (3.10), we have
$\Phi_+(y_+,x_+):=\left(\Phi_+^1(y_+,x_+),\Phi_+^2(y_+,x_+)\right)$, by (3.10), we have
 \begin{align*}
\left(\begin{array}{c}
\dot{y}\\
\dot{x}
\end{array}\right)=\left(\begin{array}{cc}
(\partial_{y_+} \Phi_{+}^1)\dot{y}_{+}&(\partial_{x_+} \Phi_{+}^1)\dot{x}_{+}\\
(\partial_{y_+} \Phi_{+}^2)\dot{y}_{+}&(\partial_{x_+} \Phi_{+}^2)\dot{x}_{+}
\end{array}\right)=D\Phi_{+}\left(\begin{array}{c}
\dot{y}_{+}\\
\dot{x}_{+}
\end{array}\right),
\end{align*}
\begin{align*}
\left(\begin{array}{c}
\dot{y}\\
\dot{x}
\end{array}\right)=\left(\begin{array}{cc}
(\partial_{y_+} \Phi_{+}^1)\dot{y}_{+}&(\partial_{x_+} \Phi_{+}^1)\dot{x}_{+}\\
(\partial_{y_+} \Phi_{+}^2)\dot{y}_{+}&(\partial_{x_+} \Phi_{+}^2)\dot{x}_{+}
\end{array}\right)=D\Phi_{+}\left(\begin{array}{c}
\dot{y}_{+}\\
\dot{x}_{+}
\end{array}\right),
\end{align*} \begin{align*}
\left(\begin{array}{c}
\partial_{y_{+}} H\\
\partial_{x_{+}} H
\end{array}\right)&=\left(\begin{array}{cc}
\partial_{y} H\partial_{y_+} y&\partial_{x} H\partial_{y_+} x\\
\partial_{y} H\partial_{x_+} y&\partial_{x} H\partial_{x_+} x
\end{array}\right)
=\left(\begin{array}{cc}
\partial_{y_+} \Phi_+^1&\partial_{y_+} \Phi_+^2\\
\partial_{x_+} \Phi_+^1&\partial_{x_+} \Phi_+^2
\end{array}\right)
\left(\begin{array}{cc}
\partial_y H\\
\partial_x H
\end{array}\right)\\
&=D\Phi_{+}^\top\left(\begin{array}{cc}
\partial_y H\\
\partial_x H
\end{array}\right).
\end{align*}
\begin{align*}
\left(\begin{array}{c}
\partial_{y_{+}} H\\
\partial_{x_{+}} H
\end{array}\right)&=\left(\begin{array}{cc}
\partial_{y} H\partial_{y_+} y&\partial_{x} H\partial_{y_+} x\\
\partial_{y} H\partial_{x_+} y&\partial_{x} H\partial_{x_+} x
\end{array}\right)
=\left(\begin{array}{cc}
\partial_{y_+} \Phi_+^1&\partial_{y_+} \Phi_+^2\\
\partial_{x_+} \Phi_+^1&\partial_{x_+} \Phi_+^2
\end{array}\right)
\left(\begin{array}{cc}
\partial_y H\\
\partial_x H
\end{array}\right)\\
&=D\Phi_{+}^\top\left(\begin{array}{cc}
\partial_y H\\
\partial_x H
\end{array}\right).
\end{align*}Then this together with (3.9) yields
 \begin{align*}
\left(\begin{array}{c}
\dot{y}_{+}\\
\dot{x}_{+}
\end{array}\right)&=D\Phi_{+}^{-1}\left(\begin{array}{c}
\dot{y}\\
\dot{x}
\end{array}\right)
=D\Phi_{+}^{-1}J\left(\begin{array}{cc}
\partial_y H\\
\partial_x H
\end{array}\right)
=D\Phi_{+}^{-1}J(D\Phi_{+}^{-1})^\top\left(\begin{array}{c}
\partial_{y_{+}} H\\
\partial_{x_{+}} H
\end{array}\right)\\
&
=J\left(\begin{array}{c}
\partial_{y_{+}} H\\
\partial_{x_{+}} H
\end{array}\right),\\
\end{align*}
\begin{align*}
\left(\begin{array}{c}
\dot{y}_{+}\\
\dot{x}_{+}
\end{array}\right)&=D\Phi_{+}^{-1}\left(\begin{array}{c}
\dot{y}\\
\dot{x}
\end{array}\right)
=D\Phi_{+}^{-1}J\left(\begin{array}{cc}
\partial_y H\\
\partial_x H
\end{array}\right)
=D\Phi_{+}^{-1}J(D\Phi_{+}^{-1})^\top\left(\begin{array}{c}
\partial_{y_{+}} H\\
\partial_{x_{+}} H
\end{array}\right)\\
&
=J\left(\begin{array}{c}
\partial_{y_{+}} H\\
\partial_{x_{+}} H
\end{array}\right),\\
\end{align*}where J is the standard symplectic matrix, i.e.,
 \begin{align*}
J=\left(\begin{array}{cc}
0&-I_n\\
I_n&0
\end{array}\right).
\end{align*}
\begin{align*}
J=\left(\begin{array}{cc}
0&-I_n\\
I_n&0
\end{array}\right).
\end{align*}This finishes the proof of (3.12).
Next, we show the detailed construction of ![]() $\Phi_+$ and the estimates of
$\Phi_+$ and the estimates of ![]() $P_+$.
$P_+$.
3.2.3. Truncation
Consider the Taylor-Fourier series of P:
 \begin{equation*}
P=\sum_{k\in \mathbb{Z}^n,~\imath\in \mathbb{Z}_+^n}p_{k\imath}y^{\imath}e^{\sqrt{-1}\langle k,x\rangle},
\end{equation*}
\begin{equation*}
P=\sum_{k\in \mathbb{Z}^n,~\imath\in \mathbb{Z}_+^n}p_{k\imath}y^{\imath}e^{\sqrt{-1}\langle k,x\rangle},
\end{equation*}and let R be the truncation of P of the form
 \begin{equation*}
R=\sum_{\vert k\vert\leq K_+,~\vert\imath\vert\leq m}p_{k\imath}y^{\imath}e^{\sqrt{-1}\langle k,x\rangle}.
\end{equation*}
\begin{equation*}
R=\sum_{\vert k\vert\leq K_+,~\vert\imath\vert\leq m}p_{k\imath}y^{\imath}e^{\sqrt{-1}\langle k,x\rangle}.
\end{equation*}Remark 3.2. As demonstrated in [Reference Pöschel30], truncating y to first order is feasible. When proving theorem 2.1 in this paper, truncating y to first order is permissible (i.e., m = 1), though truncating to higher orders is also valid. However, in proving theorem 2.5, truncating y to higher orders is necessary (i.e., ![]() $m\geq\beta+1$); see (5.12) in subsection 5.1. Because we regard the action variable as the parameter in proving theorem 2.5, and the translation of the parameter is equivalent to the translation of the action variable, we need the integer
$m\geq\beta+1$); see (5.12) in subsection 5.1. Because we regard the action variable as the parameter in proving theorem 2.5, and the translation of the parameter is equivalent to the translation of the action variable, we need the integer ![]() $m\geq\beta+1$ to ensure that the translated action variable y does not run out of the given domain. Here, to make the KAM steps applicable to both theorems, we truncated y to higher orders. In this paper, we denote the order of truncation as m, which provides a more general description of the KAM iteration, clarifying how estimates vary with truncation and demonstrating the role of higher-order terms in the normal form, even though it may make the proof appear somewhat more complicated.
$m\geq\beta+1$ to ensure that the translated action variable y does not run out of the given domain. Here, to make the KAM steps applicable to both theorems, we truncated y to higher orders. In this paper, we denote the order of truncation as m, which provides a more general description of the KAM iteration, clarifying how estimates vary with truncation and demonstrating the role of higher-order terms in the normal form, even though it may make the proof appear somewhat more complicated.
Next, we will prove that the norm of P − R is much smaller than the norm of P by selecting truncation appropriately, see lemma below.
Lemma 3.3. Assume that
 \begin{align*}
{\mathbf{(H1)}}: \int_{K_+}^{\infty}t^{n}e^{-t\frac{r-r_+}{16}}dt\leq\mu.
\end{align*}
\begin{align*}
{\mathbf{(H1)}}: \int_{K_+}^{\infty}t^{n}e^{-t\frac{r-r_+}{16}}dt\leq\mu.
\end{align*}Then there is a constant c 1 such that
 \begin{align}
\left\vert\left\|P-R\right\|\right\vert_{D_\alpha}&\leq c_1\gamma_0^{n+m+2}s^m\mu^2,
\end{align}
\begin{align}
\left\vert\left\|P-R\right\|\right\vert_{D_\alpha}&\leq c_1\gamma_0^{n+m+2}s^m\mu^2,
\end{align} \begin{align}
\left\vert\left\|R\right\|\right\vert_{D_\alpha}&\leq c_1\gamma_0^{n+m+2}s^m\mu.
\end{align}
\begin{align}
\left\vert\left\|R\right\|\right\vert_{D_\alpha}&\leq c_1\gamma_0^{n+m+2}s^m\mu.
\end{align}Proof. Denote
 \begin{align*}
I&=\sum_{\vert k\vert \gt K_+,~\imath\in \mathbb{Z}_+^n}p_{k\imath}y^{\imath} e^{\sqrt{-1}\langle k,x\rangle},\\
II&=\sum_{\vert k\vert\leq K_+,~\vert\imath\vert \gt m}p_{k\imath}y^{\imath} e^{\sqrt{-1}\langle k,x\rangle}.
\end{align*}
\begin{align*}
I&=\sum_{\vert k\vert \gt K_+,~\imath\in \mathbb{Z}_+^n}p_{k\imath}y^{\imath} e^{\sqrt{-1}\langle k,x\rangle},\\
II&=\sum_{\vert k\vert\leq K_+,~\vert\imath\vert \gt m}p_{k\imath}y^{\imath} e^{\sqrt{-1}\langle k,x\rangle}.
\end{align*}Then
To estimate I, we note by (3.8) that
 \begin{align}
\left\vert\sum_{\imath\in \mathbb{Z}_+^n}p_{k\imath}y^{\imath}\right\vert\leq \left\vert P\right\vert_{D(s,r)}e^{-\vert k\vert r}\leq\gamma_0^{n+m+2}s^{m}\mu e^{-\vert k\vert r},
\end{align}
\begin{align}
\left\vert\sum_{\imath\in \mathbb{Z}_+^n}p_{k\imath}y^{\imath}\right\vert\leq \left\vert P\right\vert_{D(s,r)}e^{-\vert k\vert r}\leq\gamma_0^{n+m+2}s^{m}\mu e^{-\vert k\vert r},
\end{align} where the first inequality has been frequently used in [Reference Chow, Li and Yi10, Reference Cong, Küpper, Li and You11, Reference Han, Li and Yi17, Reference Li and Yi22, Reference Pöschel30–Reference Qian, Li and Yang32, Reference Salamon35] and the detailed proof see [Reference Salamon35]. This together with ![]() ${\mathbf{(H1)}}$ yields
${\mathbf{(H1)}}$ yields
 \begin{align}
\left\vert I\right\vert_{\hat D}&\leq\sum_{\vert k\vert \gt K_+}\left\vert\sum_{\imath\in \mathbb{Z}_+^n}p_{k\imath}y^{\imath}\right\vert e^{\vert k\vert(\frac{r_+}{8}+\frac{7r}{8})}
\leq\sum_{\vert k\vert \gt K_+}\left\vert P\right\vert _{D(s,r)}e^{-\vert k\vert\frac{r-r_+}{8}}\notag\\
&\leq\gamma_0^{n+m+2}s^{m}\mu\sum_{\kappa=K_+}^{\infty}\kappa^{n}e^{-\kappa\frac{r-r_+}{8}}
\leq\gamma_0^{n+m+2}s^{m}\mu\int_{K_+}^{\infty}t^{n}e^{-t\frac{r-r_+}{16}}dt\\
&\leq\gamma_0^{n+m+2}s^{m}\mu^2\notag
\end{align}
\begin{align}
\left\vert I\right\vert_{\hat D}&\leq\sum_{\vert k\vert \gt K_+}\left\vert\sum_{\imath\in \mathbb{Z}_+^n}p_{k\imath}y^{\imath}\right\vert e^{\vert k\vert(\frac{r_+}{8}+\frac{7r}{8})}
\leq\sum_{\vert k\vert \gt K_+}\left\vert P\right\vert _{D(s,r)}e^{-\vert k\vert\frac{r-r_+}{8}}\notag\\
&\leq\gamma_0^{n+m+2}s^{m}\mu\sum_{\kappa=K_+}^{\infty}\kappa^{n}e^{-\kappa\frac{r-r_+}{8}}
\leq\gamma_0^{n+m+2}s^{m}\mu\int_{K_+}^{\infty}t^{n}e^{-t\frac{r-r_+}{16}}dt\\
&\leq\gamma_0^{n+m+2}s^{m}\mu^2\notag
\end{align}It follows from (3.8) and (3.16) that
 \begin{align*}
\left\vert P-I\right\vert_{\hat D}\leq\vert P\vert_{D(s,r)}+\vert I\vert_{\hat D}\leq2\gamma_0^{n+m+2}s^{m}\mu.
\end{align*}
\begin{align*}
\left\vert P-I\right\vert_{\hat D}\leq\vert P\vert_{D(s,r)}+\vert I\vert_{\hat D}\leq2\gamma_0^{n+m+2}s^{m}\mu.
\end{align*} For ![]() $\vert p\vert=m+1$, let
$\vert p\vert=m+1$, let ![]() $\int$ be the obvious antiderivative of
$\int$ be the obvious antiderivative of  $\frac{\partial^{p}}{\partial y^p}$. Then the Cauchy estimate of P − I on Dα yields
$\frac{\partial^{p}}{\partial y^p}$. Then the Cauchy estimate of P − I on Dα yields
 \begin{align*}
\left\vert II\right\vert_{D_\alpha}&=\left\vert\int\frac{\partial^{p}}{\partial y^p}\sum_{\vert k\vert\leq K_+,~\vert\imath\vert \gt m}p_{k\imath}y^{\imath} e^{\sqrt{-1}\langle k,x\rangle}dy\right\vert_{D_{\alpha}}\\
&\leq\left\vert\int\left\vert\frac{\partial^{p}}{\partial y^p}(P-I)\right\vert dy\right\vert_{D_{\alpha}}\\
&\leq\left\vert\frac{c}{s^{m+1}}\int\left\vert P-I\right\vert_{\hat{D}}dy\right\vert_{D_{\alpha}}\\
&\leq2\frac{c}{s^{m+1}}\gamma_0^{n+m+2}s^{m}\mu(\alpha s)^{m+1}\\
&\leq c\gamma_0^{n+m+2}s^{m}\mu^2.
\end{align*}
\begin{align*}
\left\vert II\right\vert_{D_\alpha}&=\left\vert\int\frac{\partial^{p}}{\partial y^p}\sum_{\vert k\vert\leq K_+,~\vert\imath\vert \gt m}p_{k\imath}y^{\imath} e^{\sqrt{-1}\langle k,x\rangle}dy\right\vert_{D_{\alpha}}\\
&\leq\left\vert\int\left\vert\frac{\partial^{p}}{\partial y^p}(P-I)\right\vert dy\right\vert_{D_{\alpha}}\\
&\leq\left\vert\frac{c}{s^{m+1}}\int\left\vert P-I\right\vert_{\hat{D}}dy\right\vert_{D_{\alpha}}\\
&\leq2\frac{c}{s^{m+1}}\gamma_0^{n+m+2}s^{m}\mu(\alpha s)^{m+1}\\
&\leq c\gamma_0^{n+m+2}s^{m}\mu^2.
\end{align*}Thus,
 \begin{align}
\left\vert P-R\right\vert_{D_\alpha}=\left\vert I+II\right\vert_{D_\alpha}\leq c\gamma_0^{n+m+2}s^{m}\mu^2,
\end{align}
\begin{align}
\left\vert P-R\right\vert_{D_\alpha}=\left\vert I+II\right\vert_{D_\alpha}\leq c\gamma_0^{n+m+2}s^{m}\mu^2,
\end{align}and therefore,
 \begin{align}
\left\vert R\right\vert_{D_\alpha}\leq\vert P-R\vert_{D_\alpha}+\vert P\vert_{D(s,r)}\leq c\gamma_0^{n+m+2}s^{m}\mu.
\end{align}
\begin{align}
\left\vert R\right\vert_{D_\alpha}\leq\vert P-R\vert_{D_\alpha}+\vert P\vert_{D(s,r)}\leq c\gamma_0^{n+m+2}s^{m}\mu.
\end{align} Next, we estimate ![]() $\left\|P-R\right\|_{C^\beta}$. In view of the definition of
$\left\|P-R\right\|_{C^\beta}$. In view of the definition of ![]() $\|\cdot\|_{C^\beta}$, for
$\|\cdot\|_{C^\beta}$, for ![]() $\forall y,x\in D_\alpha$, we have
$\forall y,x\in D_\alpha$, we have
 \begin{align}
\left\|P-R\right\|_{C^\beta}&=\sup_{\xi\neq\zeta}\frac{\left\vert P(x,y,\xi)-R(x,y,\xi)-(P(x,y,\zeta)-R(x,y,\zeta))\right\vert}{\left\vert\xi-\zeta\right\vert^\beta}\notag\\
&\leq\sup_{\xi\neq\zeta}\frac{\left\vert\int\right\vert\frac{\partial^p}{\partial y^p}(P(x,y,\xi)-R(x,y,\xi)-(P(x,y,\zeta)-R(x,y,\zeta)))\left\vert dy\right\vert}{\vert\xi-\zeta\vert^\beta}\notag\\
&\leq\sup_{\xi\neq\zeta}\frac{\left\vert\frac{c}{s^{m+2}}\int\left\vert P(x,y,\xi)-P(x,y,\zeta)\right\vert dy\right\vert}{\vert\xi-\zeta\vert^\beta}\notag\\
&\leq\sup_{\xi\neq\zeta}\frac{c}{s^{m+1}}\frac{\vert P(x,y,\xi)-P(x,y,\zeta)\vert}{\vert\xi-\zeta\vert^\beta}(\alpha s)^{m+1}\notag\\
&\leq c\mu\|P\|_{C^\beta}\leq c\gamma_0^{n+m+2}s^m\mu^2,
\end{align}
\begin{align}
\left\|P-R\right\|_{C^\beta}&=\sup_{\xi\neq\zeta}\frac{\left\vert P(x,y,\xi)-R(x,y,\xi)-(P(x,y,\zeta)-R(x,y,\zeta))\right\vert}{\left\vert\xi-\zeta\right\vert^\beta}\notag\\
&\leq\sup_{\xi\neq\zeta}\frac{\left\vert\int\right\vert\frac{\partial^p}{\partial y^p}(P(x,y,\xi)-R(x,y,\xi)-(P(x,y,\zeta)-R(x,y,\zeta)))\left\vert dy\right\vert}{\vert\xi-\zeta\vert^\beta}\notag\\
&\leq\sup_{\xi\neq\zeta}\frac{\left\vert\frac{c}{s^{m+2}}\int\left\vert P(x,y,\xi)-P(x,y,\zeta)\right\vert dy\right\vert}{\vert\xi-\zeta\vert^\beta}\notag\\
&\leq\sup_{\xi\neq\zeta}\frac{c}{s^{m+1}}\frac{\vert P(x,y,\xi)-P(x,y,\zeta)\vert}{\vert\xi-\zeta\vert^\beta}(\alpha s)^{m+1}\notag\\
&\leq c\mu\|P\|_{C^\beta}\leq c\gamma_0^{n+m+2}s^m\mu^2,
\end{align}where the third inequality follows from Cauchy estimate and the last inequality follows from (3.8).
Similarly, we get
 \begin{align}
\|R\|_{C^\beta} \lt \|P-R\|_{C^\beta}+\|P\|_{C^\beta}\leq c\gamma_0^{n+m+2}s^m\mu.
\end{align}
\begin{align}
\|R\|_{C^\beta} \lt \|P-R\|_{C^\beta}+\|P\|_{C^\beta}\leq c\gamma_0^{n+m+2}s^m\mu.
\end{align}It follows from (3.17), (3.18), (3.19) and (3.20) that (3.13) and (3.14) hold.
This completes the proof.
3.2.4. Homological equation
As usual, we shall construct a symplectic transformation as the time-1 map ![]() $\phi_{F}^1$ of the flow generated by a Hamiltonian F to eliminate all resonant terms in R, i.e., all terms
$\phi_{F}^1$ of the flow generated by a Hamiltonian F to eliminate all resonant terms in R, i.e., all terms
 \begin{align*}
p_{k\imath}y^{\imath}e^{\sqrt{-1}\langle k,x\rangle},~~~~0 \lt \vert k\vert\leq K_+,\vert\imath\vert\leq m.
\end{align*}
\begin{align*}
p_{k\imath}y^{\imath}e^{\sqrt{-1}\langle k,x\rangle},~~~~0 \lt \vert k\vert\leq K_+,\vert\imath\vert\leq m.
\end{align*}To do so, we first construct a Hamiltonian F of the form
 \begin{equation}
F=\sum_{0 \lt \vert k\vert\leq K_+,\vert\imath\vert\leq m}f_{k\imath}y^{\imath}e^{\sqrt{-1}\langle k,x\rangle},
\end{equation}
\begin{equation}
F=\sum_{0 \lt \vert k\vert\leq K_+,\vert\imath\vert\leq m}f_{k\imath}y^{\imath}e^{\sqrt{-1}\langle k,x\rangle},
\end{equation}satisfying the equation
where  $[R]=\frac{1}{(2\pi)^n}\int_{T^n}R(y,x)dx$ is the average of the truncation R.
$[R]=\frac{1}{(2\pi)^n}\int_{T^n}R(y,x)dx$ is the average of the truncation R.
Substituting (3.21) into (3.22) yields that
 \begin{align*}
&-\sum_{0 \lt \vert k\vert \lt K_+,\vert\imath\vert\leq m}\sqrt{-1}\left\langle k,\omega(\xi)+\partial_y\bar{h}\right\rangle f_{k\imath}y^\imath e^{\sqrt{-1}\langle k,x\rangle}\\
&+\sum_{0 \lt \vert k\vert \lt K_+,\vert\imath\vert\leq m} p_{k\imath}y^\imath e^{\sqrt{-1}\langle k,x\rangle}=0.
\end{align*}
\begin{align*}
&-\sum_{0 \lt \vert k\vert \lt K_+,\vert\imath\vert\leq m}\sqrt{-1}\left\langle k,\omega(\xi)+\partial_y\bar{h}\right\rangle f_{k\imath}y^\imath e^{\sqrt{-1}\langle k,x\rangle}\\
&+\sum_{0 \lt \vert k\vert \lt K_+,\vert\imath\vert\leq m} p_{k\imath}y^\imath e^{\sqrt{-1}\langle k,x\rangle}=0.
\end{align*}By comparing the coefficients above, we then obtain the following quasi-linear equations:
 \begin{equation}
\sqrt{-1}\left\langle k,\omega(\xi)+\partial_y\bar{h}\right\rangle f_{k\imath}=p_{k\imath},~~~\vert\imath\vert\leq m,~~~0 \lt \vert k\vert\leq K_+.
\end{equation}
\begin{equation}
\sqrt{-1}\left\langle k,\omega(\xi)+\partial_y\bar{h}\right\rangle f_{k\imath}=p_{k\imath},~~~\vert\imath\vert\leq m,~~~0 \lt \vert k\vert\leq K_+.
\end{equation}We declare that the quasi-linear equations (3.23) are solvable under some suitable conditions. The details can be seen in the following lemma:
Lemma 3.4. Assume that
 \begin{align*}
&{\mathbf{(H2)}}: max_{\vert i\vert\leq 2}\left\vert\left\| \partial_y^i\bar{h}- \partial_y^i\bar{h}_0\right\|\right\vert_{D(s)}\leq \mu_0^{\frac{1}{2}}, \\
&{\mathbf{(H3)}}:3s \lt \frac{\gamma_0}{(M^*+2)K_+^{\tau+1}},
\end{align*}
\begin{align*}
&{\mathbf{(H2)}}: max_{\vert i\vert\leq 2}\left\vert\left\| \partial_y^i\bar{h}- \partial_y^i\bar{h}_0\right\|\right\vert_{D(s)}\leq \mu_0^{\frac{1}{2}}, \\
&{\mathbf{(H3)}}:3s \lt \frac{\gamma_0}{(M^*+2)K_+^{\tau+1}},
\end{align*}where
 \begin{align*}
{M^*=\max_{\vert i\vert\leq 2, y\in D(s)}\left\vert \partial_{y}^i\bar h_0(y,\xi_0)\right\vert.}
\end{align*}
\begin{align*}
{M^*=\max_{\vert i\vert\leq 2, y\in D(s)}\left\vert \partial_{y}^i\bar h_0(y,\xi_0)\right\vert.}
\end{align*} Then the quasi-linear equations (3.23) can be uniquely solved on D(s) to obtain a family of functions ![]() $f_{k\imath}$ which are analytic in y, Hölder continuous about ξ with Hölder index β, and satisfy the following properties:
$f_{k\imath}$ which are analytic in y, Hölder continuous about ξ with Hölder index β, and satisfy the following properties:
 \begin{equation}
\left\vert\left\|\partial_y^if_{k\imath}\right\|\right\vert_{D(s)}\leq c_2|k|^{(\vert i\vert+1)\tau+\vert i\vert}\gamma_0^{n+m+1-\vert i\vert}s^{m-\vert\imath\vert}\mu e^{-\vert k\vert r},
\end{equation}
\begin{equation}
\left\vert\left\|\partial_y^if_{k\imath}\right\|\right\vert_{D(s)}\leq c_2|k|^{(\vert i\vert+1)\tau+\vert i\vert}\gamma_0^{n+m+1-\vert i\vert}s^{m-\vert\imath\vert}\mu e^{-\vert k\vert r},
\end{equation} for all ![]() $\vert\imath\vert\leq m, 0 \lt \vert k\vert\leq K_+, \vert i\vert\leq 2$, where c 2 is a constant.
$\vert\imath\vert\leq m, 0 \lt \vert k\vert\leq K_+, \vert i\vert\leq 2$, where c 2 is a constant.
Proof. For ![]() $\forall y\in D(s)$, by
$\forall y\in D(s)$, by ![]() $\mathbf{(H2)},\mathbf{(H3)}$, we have
$\mathbf{(H2)},\mathbf{(H3)}$, we have
 \begin{equation*}
\left\vert\partial_y\bar h\right\vert_{D(s)}=\left\vert(\partial_y\bar h-\partial_y\bar h_0)+\partial_y\bar h_0\right\vert_{D(s)}
\leq(1+M^*)\vert y\vert \lt (1+M^*)s \lt \frac{\gamma_0}{3\vert k\vert^{\tau+1}}
\end{equation*}
\begin{equation*}
\left\vert\partial_y\bar h\right\vert_{D(s)}=\left\vert(\partial_y\bar h-\partial_y\bar h_0)+\partial_y\bar h_0\right\vert_{D(s)}
\leq(1+M^*)\vert y\vert \lt (1+M^*)s \lt \frac{\gamma_0}{3\vert k\vert^{\tau+1}}
\end{equation*}and
 \begin{equation*}
\left\|\partial_y\bar h\right\|_{C^\beta}=\sup_{\xi_*\neq\xi_{**},~\xi_*,\xi_{**}\in{O}}\frac{\left\vert\partial_y\bar h(y,\xi_*)-\partial_y\bar h(y,\xi_{**})\right\vert}{\vert\xi_*-\xi_{**}\vert^\beta}\leq\mu_0^\frac{1}{2}\vert y\vert \lt \vert s\vert \lt \frac{\gamma_0}{3\vert k\vert^{\tau+1}},
\end{equation*}
\begin{equation*}
\left\|\partial_y\bar h\right\|_{C^\beta}=\sup_{\xi_*\neq\xi_{**},~\xi_*,\xi_{**}\in{O}}\frac{\left\vert\partial_y\bar h(y,\xi_*)-\partial_y\bar h(y,\xi_{**})\right\vert}{\vert\xi_*-\xi_{**}\vert^\beta}\leq\mu_0^\frac{1}{2}\vert y\vert \lt \vert s\vert \lt \frac{\gamma_0}{3\vert k\vert^{\tau+1}},
\end{equation*}which imply that
 \begin{equation}
\left\vert\left\|\partial_y\bar{h}\right\|\right\vert_{D(s)} \lt \frac{\gamma_0}{3\vert k\vert^{\tau+1}}.
\end{equation}
\begin{equation}
\left\vert\left\|\partial_y\bar{h}\right\|\right\vert_{D(s)} \lt \frac{\gamma_0}{3\vert k\vert^{\tau+1}}.
\end{equation} It follows from (3.25) and ![]() $\mathrm{(A2)}$ that for
$\mathrm{(A2)}$ that for ![]() $\xi\in O$,
$\xi\in O$, ![]() $y\in D(s)$,
$y\in D(s)$, ![]() $0 \lt |k|\leq K_+$,
$0 \lt |k|\leq K_+$,
 \begin{align}
\left\vert \left\langle k,\omega(\xi)+\partial_y \bar h(y)\right\rangle\right\vert&\geq\left\vert\left\langle k,\omega(\xi_\nu) \right\rangle\right\vert -\left\vert\left\langle k,\omega(\xi)-\omega(\xi_\nu) \right\rangle\right\vert -\left\vert\left\langle k,\partial_y \bar h(y) \right\rangle\right\vert \notag\\
& \gt \frac{\gamma_0}{\vert k\vert^\tau}-\frac{\gamma_0}{3\vert k\vert^\tau}-\frac{\gamma_0}{3\vert k\vert^\tau}=\frac{\gamma_0}{3\vert k\vert^\tau}.
\end{align}
\begin{align}
\left\vert \left\langle k,\omega(\xi)+\partial_y \bar h(y)\right\rangle\right\vert&\geq\left\vert\left\langle k,\omega(\xi_\nu) \right\rangle\right\vert -\left\vert\left\langle k,\omega(\xi)-\omega(\xi_\nu) \right\rangle\right\vert -\left\vert\left\langle k,\partial_y \bar h(y) \right\rangle\right\vert \notag\\
& \gt \frac{\gamma_0}{\vert k\vert^\tau}-\frac{\gamma_0}{3\vert k\vert^\tau}-\frac{\gamma_0}{3\vert k\vert^\tau}=\frac{\gamma_0}{3\vert k\vert^\tau}.
\end{align}Hence
 \begin{equation}
L_k=\sqrt{-1}\left\langle k,\omega(\xi)+\partial_y\bar h(y)\right\rangle
\end{equation}
\begin{equation}
L_k=\sqrt{-1}\left\langle k,\omega(\xi)+\partial_y\bar h(y)\right\rangle
\end{equation}is invertible, and
 \begin{equation}
f_{k\imath}=L_k^{-1} p_{k\imath},
\end{equation}
\begin{equation}
f_{k\imath}=L_k^{-1} p_{k\imath},
\end{equation} for all ![]() $y\in D(s)$,
$y\in D(s)$, ![]() $\xi\in O$,
$\xi\in O$, ![]() $0 \lt \vert k\vert\leq K_+$,
$0 \lt \vert k\vert\leq K_+$, ![]() $\vert\imath\vert\leq m$. The analyticity of
$\vert\imath\vert\leq m$. The analyticity of ![]() $\bar h(y)$ and
$\bar h(y)$ and ![]() $p_{k\imath}$ implies that
$p_{k\imath}$ implies that ![]() $f_{k\imath}$ is analytic with respect to y. It follows from (3.23) that the Hölder continuity of
$f_{k\imath}$ is analytic with respect to y. It follows from (3.23) that the Hölder continuity of ![]() $f_{k\imath}$ with respect to the parameter ξ is determined by
$f_{k\imath}$ with respect to the parameter ξ is determined by ![]() $\omega(\xi)$,
$\omega(\xi)$, ![]() $\bar{h}$ and
$\bar{h}$ and ![]() $p_{k\imath}$, which are Hölder continuous about parameter ξ with Hölder index β. Let
$p_{k\imath}$, which are Hölder continuous about parameter ξ with Hölder index β. Let ![]() $0 \lt \vert k\vert\leq K_+$. We note by the first inequality of (3.15) and Cauchy estimate that
$0 \lt \vert k\vert\leq K_+$. We note by the first inequality of (3.15) and Cauchy estimate that
 \begin{align}
\left\vert\left\|p_{k\imath}\right\|\right\vert_{D(s)}&\leq\left\vert\left\| \partial_y^\imath P\right\|\right\vert_{\tilde{D}}e^{-\vert k\vert r}\leq\gamma_0^{n+m+2}s^{m-\vert\imath\vert}\mu e^{-\vert k\vert r},~~~~\vert\imath\vert\leq m,
\end{align}
\begin{align}
\left\vert\left\|p_{k\imath}\right\|\right\vert_{D(s)}&\leq\left\vert\left\| \partial_y^\imath P\right\|\right\vert_{\tilde{D}}e^{-\vert k\vert r}\leq\gamma_0^{n+m+2}s^{m-\vert\imath\vert}\mu e^{-\vert k\vert r},~~~~\vert\imath\vert\leq m,
\end{align} \begin{align*}
\left\vert\left\|L_k^{-1}\right\|\right\vert_{D(s)}&\leq c\frac{\vert k\vert^{2\tau+1}}{\gamma_0^2},
\end{align*}
\begin{align*}
\left\vert\left\|L_k^{-1}\right\|\right\vert_{D(s)}&\leq c\frac{\vert k\vert^{2\tau+1}}{\gamma_0^2},
\end{align*}and
 \begin{align}
\left\vert\left\|\partial_y^iL_k^{-1}\right\|\right\vert_{D(s)}&\leq c_2\left\vert k\right\vert^{\vert i\vert}\left\|\left\vert L_k^{-1}\right\|\right\vert_{D(s)}^{\vert i\vert+1}\leq c_2\frac{\vert k\vert^{2(\vert i\vert+1)\tau+2\vert i\vert+1}}{\gamma_0^{2(\vert i\vert+1)}},~~~~\vert i\vert\leq2.
\end{align}
\begin{align}
\left\vert\left\|\partial_y^iL_k^{-1}\right\|\right\vert_{D(s)}&\leq c_2\left\vert k\right\vert^{\vert i\vert}\left\|\left\vert L_k^{-1}\right\|\right\vert_{D(s)}^{\vert i\vert+1}\leq c_2\frac{\vert k\vert^{2(\vert i\vert+1)\tau+2\vert i\vert+1}}{\gamma_0^{2(\vert i\vert+1)}},~~~~\vert i\vert\leq2.
\end{align}So, by (3.28), (3.29) and (3.30), we get
 \begin{align*}
\left\vert\left\| \partial_y^if_{k\imath}\right\|\right\vert_{D(s)}&\leq c_2\frac{\vert k\vert^{2(\vert i\vert+1)\tau+2\vert i\vert+1}}{\gamma_0^{2(\vert i\vert+1)}}\gamma_0^{n+m+2}s^{m-\vert\imath\vert}\mu e^{-\vert k\vert r}\\
&=c_2\vert k\vert^{2(\vert i\vert+1)\tau+2\vert i\vert+1}\gamma_0^{n+m-2\vert i\vert}s^{m-\vert\imath\vert}\mu e^{-\vert k\vert r},~~~~\vert i\vert\leq 2.
\end{align*}
\begin{align*}
\left\vert\left\| \partial_y^if_{k\imath}\right\|\right\vert_{D(s)}&\leq c_2\frac{\vert k\vert^{2(\vert i\vert+1)\tau+2\vert i\vert+1}}{\gamma_0^{2(\vert i\vert+1)}}\gamma_0^{n+m+2}s^{m-\vert\imath\vert}\mu e^{-\vert k\vert r}\\
&=c_2\vert k\vert^{2(\vert i\vert+1)\tau+2\vert i\vert+1}\gamma_0^{n+m-2\vert i\vert}s^{m-\vert\imath\vert}\mu e^{-\vert k\vert r},~~~~\vert i\vert\leq 2.
\end{align*}This completes the proof.
Next, we apply the above transformation ![]() $\phi_F^1$ to Hamiltonian H, i.e.,
$\phi_F^1$ to Hamiltonian H, i.e.,
 \begin{align*}
H\circ\phi_F^1=&(N+R)\circ\phi_F^1+(P-R)\circ\phi_F^1\\
=&(N+R)+\{N,F\}+\int_0^1\left\{(1-t)\{N,F\}+R,F\right\}\circ\phi_F^tdt\\
&+(P-R)\circ\phi_F^1\\
=&N+[R]+\int_0^1\left\{R_t,F\right\}\circ\phi_F^tdt+\left(P-R\right)\circ\phi_F^1\\
=&:N_++ P_+,
\end{align*}
\begin{align*}
H\circ\phi_F^1=&(N+R)\circ\phi_F^1+(P-R)\circ\phi_F^1\\
=&(N+R)+\{N,F\}+\int_0^1\left\{(1-t)\{N,F\}+R,F\right\}\circ\phi_F^tdt\\
&+(P-R)\circ\phi_F^1\\
=&N+[R]+\int_0^1\left\{R_t,F\right\}\circ\phi_F^tdt+\left(P-R\right)\circ\phi_F^1\\
=&:N_++ P_+,
\end{align*}where
 \begin{align}
&\omega_+=\omega_0(\xi)+\sum_{j=0}^{\nu}p_{01}^j(\xi),
\end{align}
\begin{align}
&\omega_+=\omega_0(\xi)+\sum_{j=0}^{\nu}p_{01}^j(\xi),
\end{align} \begin{align}
& P_+=\int_0^1\{R_t,F\}\circ\phi_F^tdt+(P-R)\circ\phi_F^1,\\
&R_t=(1-t)[R]+tR.\notag
\end{align}
\begin{align}
& P_+=\int_0^1\{R_t,F\}\circ\phi_F^tdt+(P-R)\circ\phi_F^1,\\
&R_t=(1-t)[R]+tR.\notag
\end{align}3.2.5. Translation
In this subsection, we will translate the parameter domain O to ![]() $O_+$ so that appropriate parameters can be found in
$O_+$ so that appropriate parameters can be found in ![]() $O_+$ to ensure the frequency remains unchanged in the next KAM step. To achieve this, we need to find an appropriate
$O_+$ to ensure the frequency remains unchanged in the next KAM step. To achieve this, we need to find an appropriate ![]() $\xi_+\in O$.
$\xi_+\in O$.
3.2.6. Frequency-preserving
In this subsection, we find the parameter ![]() $\xi_+$ such that the new frequency
$\xi_+$ such that the new frequency ![]() $\omega_+$ at
$\omega_+$ at ![]() $\xi_+$ is equal to the given frequency
$\xi_+$ is equal to the given frequency ![]() $\omega_0(\xi_0)$. Recall the topological degree condition
$\omega_0(\xi_0)$. Recall the topological degree condition ![]() $\mathrm{(A0)}$ and the weak convexity condition
$\mathrm{(A0)}$ and the weak convexity condition ![]() $\mathrm{(A1)}$. The former ensures that the parameter
$\mathrm{(A1)}$. The former ensures that the parameter ![]() $\xi_+$ can be found in the parameter set to keep the frequency unchanged at this KAM step. The latter ensures that the distance between
$\xi_+$ can be found in the parameter set to keep the frequency unchanged at this KAM step. The latter ensures that the distance between ![]() $\xi_+$ and ξ is smaller than the distance between ξ and
$\xi_+$ and ξ is smaller than the distance between ξ and ![]() $\xi_{\nu-1}$, i.e., the sequence of parameters is convergent after an infinite number of iteration steps. The following lemma is crucial to our arguments.
$\xi_{\nu-1}$, i.e., the sequence of parameters is convergent after an infinite number of iteration steps. The following lemma is crucial to our arguments.
Lemma 3.5. Assume that
 \begin{align*}
\mathbf{(H4)}:\left\vert\left\|\sum_{j=0}^{\nu}p_{01}^j\right\|\right\vert_{D(s,r)} \lt \mu_0^{\frac{1}{2}}.
\end{align*}
\begin{align*}
\mathbf{(H4)}:\left\vert\left\|\sum_{j=0}^{\nu}p_{01}^j\right\|\right\vert_{D(s,r)} \lt \mu_0^{\frac{1}{2}}.
\end{align*} There exists  $\xi_+\in B_{c\mu^{{1}/{\beta}}}(\xi_\nu)\subset O^o$ such that
$\xi_+\in B_{c\mu^{{1}/{\beta}}}(\xi_\nu)\subset O^o$ such that
Proof. The proof will be completed by an induction on ν. We start with the case ν = 0. It is obvious that ![]() $\omega_0(\xi_0)=\omega_0(\xi_0)$. Now assuming that for some ν > 0 we have
$\omega_0(\xi_0)=\omega_0(\xi_0)$. Now assuming that for some ν > 0 we have
 \begin{align}
\omega_i(\xi_i)=\omega_0(\xi_0),~~\xi_i\in B_{c\mu_{i-1}^{{1}/{\beta}}}(\xi_{i-1})\subset O^o,~~~i=1,\cdots,\nu,
\end{align}
\begin{align}
\omega_i(\xi_i)=\omega_0(\xi_0),~~\xi_i\in B_{c\mu_{i-1}^{{1}/{\beta}}}(\xi_{i-1})\subset O^o,~~~i=1,\cdots,\nu,
\end{align} where  $\omega_i(\xi)=\omega_0(\xi)+\sum_{j=0}^{i-1}p_{01}^j(\xi)$. We need to find
$\omega_i(\xi)=\omega_0(\xi)+\sum_{j=0}^{i-1}p_{01}^j(\xi)$. We need to find ![]() $\xi_+$ near ξ such that
$\xi_+$ near ξ such that
In view of the property of topological degree, ![]() ${\mathbf{(H4)}}$ and
${\mathbf{(H4)}}$ and ![]() $\mathrm{(A0)}$, we have
$\mathrm{(A0)}$, we have
 \begin{align*}
\deg\left(\omega_+(\cdot),O^o,\omega_0(\xi_0)\right)& =\deg\left(\omega_0(\cdot)+\sum_{j=0}^{\nu}p_{01}^j(\cdot),O^o,\omega_0(\xi_0)\right)\notag\\ & =\deg\left(\omega_0(\cdot),O^o,\omega_0(\xi_0)\right)\neq0,
\end{align*}
\begin{align*}
\deg\left(\omega_+(\cdot),O^o,\omega_0(\xi_0)\right)& =\deg\left(\omega_0(\cdot)+\sum_{j=0}^{\nu}p_{01}^j(\cdot),O^o,\omega_0(\xi_0)\right)\notag\\ & =\deg\left(\omega_0(\cdot),O^o,\omega_0(\xi_0)\right)\neq0,
\end{align*} i.e., there exists at least a ![]() $\xi_+\in O^o$ such that (3.36) holds.
$\xi_+\in O^o$ such that (3.36) holds.
Next, we estimate ![]() $\vert\xi_+-\xi_\nu\vert$. (3.14) in lemma 3.3 implies that
$\vert\xi_+-\xi_\nu\vert$. (3.14) in lemma 3.3 implies that
 \begin{align*}
\left\|p_{01}^j\right\|_{C^\beta} \lt c\mu_j,~~~j=0,1,\cdots,\nu,
\end{align*}
\begin{align*}
\left\|p_{01}^j\right\|_{C^\beta} \lt c\mu_j,~~~j=0,1,\cdots,\nu,
\end{align*}i.e.,
 \begin{align}
\left\vert p_{01}^j(\xi_+)-p_{01}^j(\xi_\nu)\right\vert \lt c\mu_j\left\vert\xi_+-\xi_\nu\right\vert^\beta,~~\forall\xi_+, \xi\in{O}.
\end{align}
\begin{align}
\left\vert p_{01}^j(\xi_+)-p_{01}^j(\xi_\nu)\right\vert \lt c\mu_j\left\vert\xi_+-\xi_\nu\right\vert^\beta,~~\forall\xi_+, \xi\in{O}.
\end{align}According to (3.37) and (3.38), we get
 \begin{align}
\omega_0(\xi_+)-\omega_0(\xi_\nu)+\sum_{j=0}^{\nu-1}\left(p_{01}^{j}(\xi_+)-p_{01}^j{(\xi_\nu)}\right)=-p_{01}^{\nu}(\xi_+).
\end{align}
\begin{align}
\omega_0(\xi_+)-\omega_0(\xi_\nu)+\sum_{j=0}^{\nu-1}\left(p_{01}^{j}(\xi_+)-p_{01}^j{(\xi_\nu)}\right)=-p_{01}^{\nu}(\xi_+).
\end{align} This together with ![]() $\mathrm{(A1)}$ and (3.39) yield
$\mathrm{(A1)}$ and (3.39) yield
 \begin{align}
\left\vert p_{01}^\nu(\xi_+)\right\vert&=\left\vert\omega_0(\xi_+)-\omega_0(\xi_\nu)+\sum_{j=0}^{\nu-1}\left(p_{01}^{j}(\xi_+)-p_{01}^j{(\xi_\nu)}\right)\right\vert\notag\\
&\geq\left\vert\omega_0(\xi_+)-\omega_0(\xi_\nu)\right\vert-\sum_{j=0}^{\nu-1}\left\vert p_{01}^{j}(\xi_+)-p_{01}^j{(\xi_\nu)}\right\vert\notag\\
&\geq\sigma\left\vert\xi_+-\xi_\nu\right\vert^\beta-c\sum_{j=0}^{\nu-1}\mu_j\left\vert\xi_+-\xi_\nu\right\vert^\beta\notag\\
&\geq\left(\sigma-c\sum_{j=0}^{\nu-1}\mu_j\right)\left\vert\xi_+-\xi_\nu\right\vert^\beta.
\end{align}
\begin{align}
\left\vert p_{01}^\nu(\xi_+)\right\vert&=\left\vert\omega_0(\xi_+)-\omega_0(\xi_\nu)+\sum_{j=0}^{\nu-1}\left(p_{01}^{j}(\xi_+)-p_{01}^j{(\xi_\nu)}\right)\right\vert\notag\\
&\geq\left\vert\omega_0(\xi_+)-\omega_0(\xi_\nu)\right\vert-\sum_{j=0}^{\nu-1}\left\vert p_{01}^{j}(\xi_+)-p_{01}^j{(\xi_\nu)}\right\vert\notag\\
&\geq\sigma\left\vert\xi_+-\xi_\nu\right\vert^\beta-c\sum_{j=0}^{\nu-1}\mu_j\left\vert\xi_+-\xi_\nu\right\vert^\beta\notag\\
&\geq\left(\sigma-c\sum_{j=0}^{\nu-1}\mu_j\right)\left\vert\xi_+-\xi_\nu\right\vert^\beta.
\end{align}Then, by (3.41) and (3.14) in lemma 3.3, we have
 \begin{align*}
\vert\xi_+-\xi_\nu\vert^\beta&\leq\frac{p_{01}^\nu(\xi_+)}{\sigma-c\sum_{j=0}^{\nu-1}\mu_j} \lt \frac{c\mu}{\sigma-c\sum_{j=0}^{\nu-1}\mu_j} \lt \frac{2c\mu}{\sigma},
\end{align*}
\begin{align*}
\vert\xi_+-\xi_\nu\vert^\beta&\leq\frac{p_{01}^\nu(\xi_+)}{\sigma-c\sum_{j=0}^{\nu-1}\mu_j} \lt \frac{c\mu}{\sigma-c\sum_{j=0}^{\nu-1}\mu_j} \lt \frac{2c\mu}{\sigma},
\end{align*} which implies  $\xi_+\in B_{c\mu^{{1}/{\beta}}}(\xi_\nu)$. From
$\xi_+\in B_{c\mu^{{1}/{\beta}}}(\xi_\nu)$. From ![]() $\xi\in O^o$ in (3.37) and the fact that ɛ is small enough (i.e., µ is small enough), we have
$\xi\in O^o$ in (3.37) and the fact that ɛ is small enough (i.e., µ is small enough), we have  $B_{c\mu^{{1}/{\beta}}}(\xi_\nu)\subset O^o$.
$B_{c\mu^{{1}/{\beta}}}(\xi_\nu)\subset O^o$.
This completes the proof.
3.2.7. Estimate on  $N_+$
$N_+$
Now, we give the estimate on the next step ![]() $N_+$.
$N_+$.
Lemma 3.6. There is a constant c 3 such that the following conclusions hold:
 \begin{align}
&\left\vert\xi_{+}-\xi_\nu\right\vert\leq c_3\mu^\frac{1}{\beta},
\end{align}
\begin{align}
&\left\vert\xi_{+}-\xi_\nu\right\vert\leq c_3\mu^\frac{1}{\beta},
\end{align} \begin{align}
&\left\vert\left\|\bar h_+-\bar h\right\|\right\vert_{D(s)}\leq
c_3s^m\mu.
\end{align}
\begin{align}
&\left\vert\left\|\bar h_+-\bar h\right\|\right\vert_{D(s)}\leq
c_3s^m\mu.
\end{align}3.2.8. Estimate on  $\Phi_+$
$\Phi_+$
Recall that F is as in (3.21) with the coefficients and its estimate given by lemma 3.4. Then, we have the following estimate on F.
Lemma 3.7. There is a constant c 4 such that for all ![]() $\vert j\vert+\vert i\vert\leq 2$,
$\vert j\vert+\vert i\vert\leq 2$,
 \begin{align}
&\left\vert\left\| \partial_x^j\partial_y^iF\right\|\right\vert_{\hat D}\leq c_4\gamma_0^{n+m-2|i|}s^{m-\vert i \vert}\mu\Gamma(r-r_+).
\end{align}
\begin{align}
&\left\vert\left\| \partial_x^j\partial_y^iF\right\|\right\vert_{\hat D}\leq c_4\gamma_0^{n+m-2|i|}s^{m-\vert i \vert}\mu\Gamma(r-r_+).
\end{align}Proof. By (3.21) and (3.24), we have
 \begin{align*}
\left\vert\left\| \partial_x^j\partial_y^iF\right\|\right\vert_{\hat D}&\leq \sum_{\vert\imath\vert\leq m,0 \lt \vert k\vert\leq K_+}\vert k\vert^j\left\vert\left\|\partial_y^i(f_{k\imath}y^\imath)\right\|\right\vert_{D(s)}e^{\vert k\vert(r_++\frac{7}{8}(r-r_+))}\\
&\leq c_4\sum_{0 \lt \vert k\vert\leq K_+}\vert k\vert^{2(|i|+1)\tau+2\vert i\vert+1+\vert j\vert}\gamma_0^{n+m-2\vert i\vert}s^{m-\vert i\vert}\mu e^{-\vert k\vert\frac{r-r_+}{8}}\\
&\leq c_4\gamma_0^{n+m-2\vert i\vert}s^{m-\vert i\vert}\mu\Gamma(r-r_+).
\end{align*}
\begin{align*}
\left\vert\left\| \partial_x^j\partial_y^iF\right\|\right\vert_{\hat D}&\leq \sum_{\vert\imath\vert\leq m,0 \lt \vert k\vert\leq K_+}\vert k\vert^j\left\vert\left\|\partial_y^i(f_{k\imath}y^\imath)\right\|\right\vert_{D(s)}e^{\vert k\vert(r_++\frac{7}{8}(r-r_+))}\\
&\leq c_4\sum_{0 \lt \vert k\vert\leq K_+}\vert k\vert^{2(|i|+1)\tau+2\vert i\vert+1+\vert j\vert}\gamma_0^{n+m-2\vert i\vert}s^{m-\vert i\vert}\mu e^{-\vert k\vert\frac{r-r_+}{8}}\\
&\leq c_4\gamma_0^{n+m-2\vert i\vert}s^{m-\vert i\vert}\mu\Gamma(r-r_+).
\end{align*}This completes the proof.
Lemma 3.8. Assume that
 \begin{align*}
&{\mathbf{(H5)}}:c_4s^{m-1}\mu\Gamma(r-r_+) \lt \frac{1}{8}(r-r_+),\\
&{\mathbf{(H6)}}:c_4s^m\mu\Gamma(r-r_+) \lt \frac{1}{8}\alpha s.
\end{align*}
\begin{align*}
&{\mathbf{(H5)}}:c_4s^{m-1}\mu\Gamma(r-r_+) \lt \frac{1}{8}(r-r_+),\\
&{\mathbf{(H6)}}:c_4s^m\mu\Gamma(r-r_+) \lt \frac{1}{8}\alpha s.
\end{align*}Then the following conclusions hold.
(1) For all
 $0\leq t\leq 1$, the mappings(3.46)
$0\leq t\leq 1$, the mappings(3.46) \begin{align}
\phi_F^t&:D_{\frac{1}{4}\alpha}\rightarrow D_{\frac{1}{2}\alpha}
\end{align}
\begin{align}
\phi_F^t&:D_{\frac{1}{4}\alpha}\rightarrow D_{\frac{1}{2}\alpha}
\end{align}are well defined.
(2)
 $\Phi_+=\phi_F^1:D_+\rightarrow D(s,r).$
$\Phi_+=\phi_F^1:D_+\rightarrow D(s,r).$(3) There is a constant c 5 such that
 \begin{align*}
\left\vert\left\|\phi_F^t-id\right\|\right\vert_{\tilde{D}}&\leq c_5\mu\Gamma(r-r_+),\\
\left\vert\left\|D\phi_F^t-Id\right\|\right\vert_{\tilde{D}}&\leq c_5\mu\Gamma(r-r_+),\\
\left\vert\left\|D^2\phi_F^t\right\|\right\vert_{\tilde{D}}&\leq c_5\mu\Gamma(r-r_+).
\end{align*}
\begin{align*}
\left\vert\left\|\phi_F^t-id\right\|\right\vert_{\tilde{D}}&\leq c_5\mu\Gamma(r-r_+),\\
\left\vert\left\|D\phi_F^t-Id\right\|\right\vert_{\tilde{D}}&\leq c_5\mu\Gamma(r-r_+),\\
\left\vert\left\|D^2\phi_F^t\right\|\right\vert_{\tilde{D}}&\leq c_5\mu\Gamma(r-r_+).
\end{align*}(4)
 \begin{align*}
\left\vert\left\|\Phi_+-id\right\|\right\vert_{\tilde{D}}&\leq c_5\mu\Gamma(r-r_+),\\
\left\vert\left\|D\Phi_+-Id\right\|\right\vert_{\tilde{D}}&\leq c_5\mu\Gamma(r-r_+),\\
\left\vert\left\|D^2\Phi_+\right\|\right\vert_{\tilde{D}}&\leq c_5\mu\Gamma(r-r_+).
\end{align*}
\begin{align*}
\left\vert\left\|\Phi_+-id\right\|\right\vert_{\tilde{D}}&\leq c_5\mu\Gamma(r-r_+),\\
\left\vert\left\|D\Phi_+-Id\right\|\right\vert_{\tilde{D}}&\leq c_5\mu\Gamma(r-r_+),\\
\left\vert\left\|D^2\Phi_+\right\|\right\vert_{\tilde{D}}&\leq c_5\mu\Gamma(r-r_+).
\end{align*}
Proof. First, we prove (1). To verify (3.46), we denote  $\phi_{F_1}^t$ and
$\phi_{F_1}^t$ and  $\phi_{F_2}^t$ as the components of
$\phi_{F_2}^t$ as the components of ![]() $\phi_{F}^t$ in the y and x planes, respectively. Let
$\phi_{F}^t$ in the y and x planes, respectively. Let ![]() $X_F=(F_y,-F_x)^\top$ be the vector field generated by F. Then
$X_F=(F_y,-F_x)^\top$ be the vector field generated by F. Then
 \begin{align}
\phi_F^t=id+\int_0^tX_F\circ \phi_F^udu,~~~~0\leq t\leq 1.
\end{align}
\begin{align}
\phi_F^t=id+\int_0^tX_F\circ \phi_F^udu,~~~~0\leq t\leq 1.
\end{align} For any  $(y,x)\in D_{\frac{1}{4}\alpha}$, we let
$(y,x)\in D_{\frac{1}{4}\alpha}$, we let ![]() $t_*=\sup\{t\in[0,1]:\phi_F^t(y,x)\in D_\alpha\}$. Then for any
$t_*=\sup\{t\in[0,1]:\phi_F^t(y,x)\in D_\alpha\}$. Then for any ![]() $0\leq t\leq t_*$, by
$0\leq t\leq t_*$, by  $(y,x)\in D_{\frac{1}{4}\alpha}$, (3.45) in lemma 3.7,
$(y,x)\in D_{\frac{1}{4}\alpha}$, (3.45) in lemma 3.7, ![]() ${\mathbf{(H5)}}$ and
${\mathbf{(H5)}}$ and ![]() ${\mathbf{(H6)}}$, we can get the following estimates:
${\mathbf{(H6)}}$, we can get the following estimates:
 \begin{align*}
\left\vert\left\|\phi_{F_1}^t(y,x)\right\|\right\vert_{D_{\frac{1}{4}\alpha}}&\leq\left\vert y\right\vert+\int_0^t\left\vert\left\|F_x\circ\phi_F^u\right\|\right\vert_{D_{\frac{1}{4}\alpha}}du\\
&\leq \frac{1}{4}\alpha s+c_4s^{m}\mu\Gamma(r-r_+)\\
& \lt \frac{3}{8}\alpha s,\\
\left\vert\left\|\phi_{F_2}^t(y,x)\right\|\right\vert_{D_{\frac{1}{4}\alpha}}&\leq\vert x\vert+\int_0^t\left\vert\left\|F_y\circ\phi_F^u\right\|\right\vert_{D_{\frac{1}{4}\alpha}}du\\
&\leq r_++\frac{1}{8}(r-r_+)+c_4s^{m-1}\mu\Gamma(r-r_+)\\
& \lt r_++\frac{2}{8}(r-r_+).
\end{align*}
\begin{align*}
\left\vert\left\|\phi_{F_1}^t(y,x)\right\|\right\vert_{D_{\frac{1}{4}\alpha}}&\leq\left\vert y\right\vert+\int_0^t\left\vert\left\|F_x\circ\phi_F^u\right\|\right\vert_{D_{\frac{1}{4}\alpha}}du\\
&\leq \frac{1}{4}\alpha s+c_4s^{m}\mu\Gamma(r-r_+)\\
& \lt \frac{3}{8}\alpha s,\\
\left\vert\left\|\phi_{F_2}^t(y,x)\right\|\right\vert_{D_{\frac{1}{4}\alpha}}&\leq\vert x\vert+\int_0^t\left\vert\left\|F_y\circ\phi_F^u\right\|\right\vert_{D_{\frac{1}{4}\alpha}}du\\
&\leq r_++\frac{1}{8}(r-r_+)+c_4s^{m-1}\mu\Gamma(r-r_+)\\
& \lt r_++\frac{2}{8}(r-r_+).
\end{align*} Thus,  $\phi_F^t\in D_{\frac{1}{2}\alpha}\subset D_\alpha$, i.e.
$\phi_F^t\in D_{\frac{1}{2}\alpha}\subset D_\alpha$, i.e. ![]() $t_*=1$ and (1) holds.
$t_*=1$ and (1) holds.
It follows from (1) that (2) holds.
We now prove (3). Using (3.45) in lemma 3.7 and (3.47), we immediately have
 \begin{align*}
\left\vert\left\|\phi_F^t-id\right\|\right\vert_{\tilde{D}}\leq c_5\mu\Gamma(r-r_+).
\end{align*}
\begin{align*}
\left\vert\left\|\phi_F^t-id\right\|\right\vert_{\tilde{D}}\leq c_5\mu\Gamma(r-r_+).
\end{align*}By (3.45) in lemma 3.7, (3.47) and Gronwall Inequality, we get
 \begin{align*}
\left\vert\left\|D\phi_F^t-Id\right\|\right\vert_{\tilde{D}}&\leq\left\vert\left\|\int_0^tDX_F\circ \phi_F^\lambda D\phi_F^\lambda d\lambda\right\|\right\vert_{\tilde{D}}\\
&\leq\int_0^t\left\vert\left\|DX_F\circ \phi_F^\lambda\right\|\right\vert_{\tilde{D}}\left\vert\left\|D\phi_F^\lambda-Id\right\|\right\vert_{\tilde{D}}d\lambda+\int_0^t\left\vert\left\|DX_F\circ \phi_F^\lambda\right\|\right\vert_{\tilde{D}}d\lambda\\
&\leq c_5\mu\Gamma(r-r_+).
\end{align*}
\begin{align*}
\left\vert\left\|D\phi_F^t-Id\right\|\right\vert_{\tilde{D}}&\leq\left\vert\left\|\int_0^tDX_F\circ \phi_F^\lambda D\phi_F^\lambda d\lambda\right\|\right\vert_{\tilde{D}}\\
&\leq\int_0^t\left\vert\left\|DX_F\circ \phi_F^\lambda\right\|\right\vert_{\tilde{D}}\left\vert\left\|D\phi_F^\lambda-Id\right\|\right\vert_{\tilde{D}}d\lambda+\int_0^t\left\vert\left\|DX_F\circ \phi_F^\lambda\right\|\right\vert_{\tilde{D}}d\lambda\\
&\leq c_5\mu\Gamma(r-r_+).
\end{align*} It follows from the induction and a similar argument that we have the estimate on the 2-order derivative of ![]() $\phi_F^t$, i.e.,
$\phi_F^t$, i.e.,
 \begin{align*}
\left\vert\left\|D^2\phi_F^t\right\|\right\vert_{\tilde{D}}\leq c_5\mu\Gamma(r-r_+).
\end{align*}
\begin{align*}
\left\vert\left\|D^2\phi_F^t\right\|\right\vert_{\tilde{D}}\leq c_5\mu\Gamma(r-r_+).
\end{align*}(4) now follows from (3).
This completes the proof.
3.2.9. Estimate on  $P_+$
$P_+$
In the following, we estimate the next step ![]() $P_+$.
$P_+$.
Lemma 3.9. Assume ![]() ${\mathbf{(H1)}}$-
${\mathbf{(H1)}}$-![]() ${\mathbf{(H6)}}$. Then there is a constant c 6 such that
${\mathbf{(H6)}}$. Then there is a constant c 6 such that
 \begin{equation}
\left\vert\left\|P_+\right\|\right\vert_{D_+}\leq c_6\gamma_0^{n+m+2}s^m\mu^2(\Gamma^2(r-r_+)+\Gamma(r-r_+)).
\end{equation}
\begin{equation}
\left\vert\left\|P_+\right\|\right\vert_{D_+}\leq c_6\gamma_0^{n+m+2}s^m\mu^2(\Gamma^2(r-r_+)+\Gamma(r-r_+)).
\end{equation}Moreover, if
then
 \begin{equation}
\left\vert\left\|P_+\right\|\right\vert_{D_+}\leq \gamma_0^{n+m+2}s_+^m\mu_+.
\end{equation}
\begin{equation}
\left\vert\left\|P_+\right\|\right\vert_{D_+}\leq \gamma_0^{n+m+2}s_+^m\mu_+.
\end{equation}Proof. By (3.13) and (3.14) in lemma 3.3, (3.45) in lemma 3.7 and lemma 3.8 (3), we have that, for all ![]() $0\leq t\leq 1$,
$0\leq t\leq 1$,
 \begin{align*}
\left\vert\left\| \{R_t,F\}\circ\phi_F^t\right\|\right\vert_{D_{\frac{1}{4}\alpha}}&\leq c\gamma_0^{n+m+2}s^m\mu^2\Gamma^2(r-r_+),\\
\left\vert\left\| (P-R)\circ\phi_F^1\right\|\right\vert_{D_{\frac{1}{4}\alpha}}&\leq c\gamma_0^{n+m+2}s^m\mu^2\Gamma(r-r_+).
\end{align*}
\begin{align*}
\left\vert\left\| \{R_t,F\}\circ\phi_F^t\right\|\right\vert_{D_{\frac{1}{4}\alpha}}&\leq c\gamma_0^{n+m+2}s^m\mu^2\Gamma^2(r-r_+),\\
\left\vert\left\| (P-R)\circ\phi_F^1\right\|\right\vert_{D_{\frac{1}{4}\alpha}}&\leq c\gamma_0^{n+m+2}s^m\mu^2\Gamma(r-r_+).
\end{align*}So, by (3.35),
 \begin{equation*}
\left\vert\left\| P_+\right\|\right\vert_{D_{\frac{1}{4}\alpha}}\leq c\gamma_0^{n+m+2}s^m\mu^2\left(\Gamma^2(r-r_+)+\Gamma(r-r_+)\right).
\end{equation*}
\begin{equation*}
\left\vert\left\| P_+\right\|\right\vert_{D_{\frac{1}{4}\alpha}}\leq c\gamma_0^{n+m+2}s^m\mu^2\left(\Gamma^2(r-r_+)+\Gamma(r-r_+)\right).
\end{equation*} By ![]() $\mathbf{(H7)}$, we see that
$\mathbf{(H7)}$, we see that
 \begin{align*}
\left\vert\left\|P_+\right\|\right\vert_{D_+}&\leq 8^mc_0\mu^{1+\rho}s_+^m\mu^{1-2\rho-\frac{m}{m+1}}\gamma_0^{n+m+2}\left(\mu^\rho\left(\Gamma^2(r-r_+)+\Gamma(r-r_+)\right)\right)\\
&\leq\gamma_0^{n+m+2}s_+^m\mu_+,
\end{align*}
\begin{align*}
\left\vert\left\|P_+\right\|\right\vert_{D_+}&\leq 8^mc_0\mu^{1+\rho}s_+^m\mu^{1-2\rho-\frac{m}{m+1}}\gamma_0^{n+m+2}\left(\mu^\rho\left(\Gamma^2(r-r_+)+\Gamma(r-r_+)\right)\right)\\
&\leq\gamma_0^{n+m+2}s_+^m\mu_+,
\end{align*}which implies (3.49).
This completes the proof.
This completes one cycle of KAM steps.
4. Proof of theorem 2.1
4.1. Iteration lemma
In this subsection, we will prove an iteration lemma which guarantees the inductive construction of the transformations in all KAM steps.
Let ![]() $r_0,s_0,\alpha_0,
\mu_0,H_0,N_0,e_0,\bar h_0,P_0$ be given at the beginning of section 3 and let
$r_0,s_0,\alpha_0,
\mu_0,H_0,N_0,e_0,\bar h_0,P_0$ be given at the beginning of section 3 and let ![]() $D_0=D(s_0,r_0)$,
$D_0=D(s_0,r_0)$, ![]() $K_0=0$,
$K_0=0$, ![]() $\Phi_0=id$. We define the following sequences inductively for all
$\Phi_0=id$. We define the following sequences inductively for all ![]() $\nu=1,2,\cdots$:
$\nu=1,2,\cdots$:
 \begin{align*}
r_\nu&=r_0\left(1-\sum_{i=1}^\nu\frac{1}{2^{i+1}}\right),\\
s_\nu&=\frac{1}{8}\alpha_{\nu-1}s_{\nu-1},\\
\alpha_\nu&=\mu_\nu^{2\rho}=\mu_\nu^{\frac{1}{m+1}},\\
\mu_\nu&=8^mc_0\mu_{\nu-1}^{1+\rho},\\
K_\nu&=\left(\left[\log\left(\frac{1}{\mu_{\nu-1}}\right)\right]+1\right)^{3\eta},\\
\tilde{D}_\nu&=D\left(\frac{1}{2} s_\nu, r_\nu+\frac{6}{8}\left(r_{\nu-1}-r_\nu\right)\right).
\end{align*}
\begin{align*}
r_\nu&=r_0\left(1-\sum_{i=1}^\nu\frac{1}{2^{i+1}}\right),\\
s_\nu&=\frac{1}{8}\alpha_{\nu-1}s_{\nu-1},\\
\alpha_\nu&=\mu_\nu^{2\rho}=\mu_\nu^{\frac{1}{m+1}},\\
\mu_\nu&=8^mc_0\mu_{\nu-1}^{1+\rho},\\
K_\nu&=\left(\left[\log\left(\frac{1}{\mu_{\nu-1}}\right)\right]+1\right)^{3\eta},\\
\tilde{D}_\nu&=D\left(\frac{1}{2} s_\nu, r_\nu+\frac{6}{8}\left(r_{\nu-1}-r_\nu\right)\right).
\end{align*}Lemma 4.1. Denote
 \begin{align*}
\mu_*=\frac{\mu_0}{\left(M^*+2\right)^{m-1}K_1^{(\tau+1)(m-1)}}.
\end{align*}
\begin{align*}
\mu_*=\frac{\mu_0}{\left(M^*+2\right)^{m-1}K_1^{(\tau+1)(m-1)}}.
\end{align*} If ɛ is small enough, then the KAM step described on the above is valid for all ![]() $\nu=0,1,\cdots$, resulting the sequences
$\nu=0,1,\cdots$, resulting the sequences
![]() $\nu=1,2,\cdots,$ with the following properties:
$\nu=1,2,\cdots,$ with the following properties:
(1)
(4.1) \begin{align}
\left\vert e_{\nu+1}-e_{\nu}\right\vert&\leq\frac{\mu_*^{\frac{1}{2}}}{2^{\nu}},
\end{align}(4.2)
\begin{align}
\left\vert e_{\nu+1}-e_{\nu}\right\vert&\leq\frac{\mu_*^{\frac{1}{2}}}{2^{\nu}},
\end{align}(4.2) \begin{align}
\left\vert e_\nu-e_{0}\right\vert&\leq2\mu_*^{\frac{1}{2}},
\end{align}(4.3)
\begin{align}
\left\vert e_\nu-e_{0}\right\vert&\leq2\mu_*^{\frac{1}{2}},
\end{align}(4.3) \begin{align}
\left\vert\left\|\bar h_{\nu+1}-\bar h_{\nu}\right\|\right\vert_{D(s_{\nu})}&\leq\frac{\mu_*^{\frac{1}{2}}}{2^{\nu}},
\end{align}(4.4)
\begin{align}
\left\vert\left\|\bar h_{\nu+1}-\bar h_{\nu}\right\|\right\vert_{D(s_{\nu})}&\leq\frac{\mu_*^{\frac{1}{2}}}{2^{\nu}},
\end{align}(4.4) \begin{align}
\left\vert\left\|\bar h_\nu-\bar h_{0}\right\|\right\vert_{D(s_\nu)}&\leq2\mu_*^{\frac{1}{2}},
\end{align}(4.5)
\begin{align}
\left\vert\left\|\bar h_\nu-\bar h_{0}\right\|\right\vert_{D(s_\nu)}&\leq2\mu_*^{\frac{1}{2}},
\end{align}(4.5) \begin{align}
\left\vert\left\|P_\nu\right\|\right\vert_{D(s_\nu,r_\nu)}&\leq\frac{\mu_*^{\frac{1}{2}}}{2^{\nu}},
\end{align}(4.6)
\begin{align}
\left\vert\left\|P_\nu\right\|\right\vert_{D(s_\nu,r_\nu)}&\leq\frac{\mu_*^{\frac{1}{2}}}{2^{\nu}},
\end{align}(4.6) \begin{align}
\left\vert\xi_{\nu+1}-\xi_{\nu}\right\vert&\leq\left(\frac{\mu_*^{\frac{1}{2}}}{2^{\nu}}\right)^{\frac{1}{\beta}}.
\end{align}
\begin{align}
\left\vert\xi_{\nu+1}-\xi_{\nu}\right\vert&\leq\left(\frac{\mu_*^{\frac{1}{2}}}{2^{\nu}}\right)^{\frac{1}{\beta}}.
\end{align}(2)
 $\Phi_{\nu+1}:\tilde{D}_{\nu+1}\rightarrow \tilde{D}_{\nu}$ is symplectic, and(4.7)
$\Phi_{\nu+1}:\tilde{D}_{\nu+1}\rightarrow \tilde{D}_{\nu}$ is symplectic, and(4.7) \begin{align}
\left\vert\left\|\Phi_{\nu+1}-id\right\|\right\vert_{\tilde{D}_{\nu+1}}\leq\frac{\mu_*^{\frac{1}{2}}}{2^{\nu}}.
\end{align}
\begin{align}
\left\vert\left\|\Phi_{\nu+1}-id\right\|\right\vert_{\tilde{D}_{\nu+1}}\leq\frac{\mu_*^{\frac{1}{2}}}{2^{\nu}}.
\end{align}Moreover, on
 $D_{\nu+1}$,
$D_{\nu+1}$,
 \begin{equation*}
H_{\nu+1}=H_\nu\circ\Phi_{\nu+1}=N_{\nu+1}+P_{\nu+1}.
\end{equation*}
\begin{equation*}
H_{\nu+1}=H_\nu\circ\Phi_{\nu+1}=N_{\nu+1}+P_{\nu+1}.
\end{equation*}
Proof. The proof amounts to the verification of ![]() $\mathbf{(H1)}$-
$\mathbf{(H1)}$-![]() $\mathbf{(H7)}$ for all ν. For simplicity, we let
$\mathbf{(H7)}$ for all ν. For simplicity, we let ![]() $r_0=1$. It follows from ɛ small enough that µ 0 is small. So, we see that
$r_0=1$. It follows from ɛ small enough that µ 0 is small. So, we see that ![]() $\mathbf{(H2)}$,
$\mathbf{(H2)}$, ![]() $\mathbf{(H4)}$-
$\mathbf{(H4)}$-![]() $\mathbf{(H7)}$ hold for ν = 0. From (3.2),
$\mathbf{(H7)}$ hold for ν = 0. From (3.2), ![]() $\mathbf{(H3)}$ holds for ν = 0. According to the definition of µν, we see that
$\mathbf{(H3)}$ holds for ν = 0. According to the definition of µν, we see that
 \begin{equation}
\mu_\nu=(8^mc_0)^{\frac{(1+\rho)^\nu-1}{\rho}}\mu_0^{(1+\rho)^\nu}.
\end{equation}
\begin{equation}
\mu_\nu=(8^mc_0)^{\frac{(1+\rho)^\nu-1}{\rho}}\mu_0^{(1+\rho)^\nu}.
\end{equation} Let ![]() $\zeta\gg1$ be fixed and µ 0 be small enough so that
$\zeta\gg1$ be fixed and µ 0 be small enough so that
 \begin{equation}
\mu_0 \lt \left(\frac{1}{8^mc_0\zeta}\right)^{\frac{1}{\rho}} \lt 1.
\end{equation}
\begin{equation}
\mu_0 \lt \left(\frac{1}{8^mc_0\zeta}\right)^{\frac{1}{\rho}} \lt 1.
\end{equation}Then
 \begin{align}
\mu_1&=8^mc_0\mu_0^{1+\rho} \lt \frac{1}{\zeta}\mu_0 \lt 1,\notag\\
\mu_2&=8^mc_0\mu_1^{1+\rho} \lt \frac{1}{\zeta}\mu_1 \lt \frac{1}{\zeta^2}\mu_0,\notag\\
\vdots\notag\\
\mu_\nu&=8^mc_0\mu_{\nu-1}^{1+\rho} \lt \cdots \lt \frac{1}{\zeta^\nu}\mu_0.
\end{align}
\begin{align}
\mu_1&=8^mc_0\mu_0^{1+\rho} \lt \frac{1}{\zeta}\mu_0 \lt 1,\notag\\
\mu_2&=8^mc_0\mu_1^{1+\rho} \lt \frac{1}{\zeta}\mu_1 \lt \frac{1}{\zeta^2}\mu_0,\notag\\
\vdots\notag\\
\mu_\nu&=8^mc_0\mu_{\nu-1}^{1+\rho} \lt \cdots \lt \frac{1}{\zeta^\nu}\mu_0.
\end{align}Denote
We notice that
 \begin{equation}
\frac{r_\nu-r_{\nu+1}}{r_0}=\frac{1}{2^{\nu+2}}.
\end{equation}
\begin{equation}
\frac{r_\nu-r_{\nu+1}}{r_0}=\frac{1}{2^{\nu+2}}.
\end{equation}Since
 \begin{align*}
\Gamma_\nu&\leq\int_1^\infty t^{6\tau+7}e^{-\frac{t}{2^{\nu+5}}}dt\\
&\leq(6\tau+7)!2^{(\nu+5)(6\tau+7)},
\end{align*}
\begin{align*}
\Gamma_\nu&\leq\int_1^\infty t^{6\tau+7}e^{-\frac{t}{2^{\nu+5}}}dt\\
&\leq(6\tau+7)!2^{(\nu+5)(6\tau+7)},
\end{align*}it is obvious that if ζ is large enough, then
which implies that ![]() $\mathbf{(H7)}$ holds for all
$\mathbf{(H7)}$ holds for all ![]() $\nu\geq1$, and
$\nu\geq1$, and
 \begin{equation}
\mu_\nu\Gamma_\nu\leq\mu_\nu^{1-\rho}\leq\frac{\mu_0^{1-\rho}}{\zeta^{(1-\rho)\nu}}.
\end{equation}
\begin{equation}
\mu_\nu\Gamma_\nu\leq\mu_\nu^{1-\rho}\leq\frac{\mu_0^{1-\rho}}{\zeta^{(1-\rho)\nu}}.
\end{equation} By (4.11) and (4.12), it is easy to verify that ![]() $\mathbf{(H5)}$ and
$\mathbf{(H5)}$ and ![]() $\mathbf{(H6)}$ hold for all
$\mathbf{(H6)}$ hold for all ![]() $\nu\geq1$ as ζ is large enough and ɛ is small enough.
$\nu\geq1$ as ζ is large enough and ɛ is small enough.
By (3.14) in lemma 3.3 and (4.10), we have
 \begin{align*}
\left\vert\left\|\sum_{j=0}^{\nu}p_{01}^j\right\|\right\vert_{D(s_\nu,r_\nu)} \lt c\sum_{j=0}^{\nu}\mu_j \lt c\sum_{j=0}^{\nu}\frac{1}{\zeta^j}\mu_0 \lt c\mu_0^{\frac{1}{2}},
\end{align*}
\begin{align*}
\left\vert\left\|\sum_{j=0}^{\nu}p_{01}^j\right\|\right\vert_{D(s_\nu,r_\nu)} \lt c\sum_{j=0}^{\nu}\mu_j \lt c\sum_{j=0}^{\nu}\frac{1}{\zeta^j}\mu_0 \lt c\mu_0^{\frac{1}{2}},
\end{align*} which implies ![]() $\mathbf{(H4)}$.
$\mathbf{(H4)}$.
To verify ![]() $\mathbf{(H3)}$, we observe by (4.8) and (4.10) that
$\mathbf{(H3)}$, we observe by (4.8) and (4.10) that
 \begin{equation*}
\frac{1}{4}\left(M^*+2\right)\mu_{\nu-1}^{2\rho}K_{\nu+1}^{\tau+1} \lt \frac{1}{2^{\nu+2}},
\end{equation*}
\begin{equation*}
\frac{1}{4}\left(M^*+2\right)\mu_{\nu-1}^{2\rho}K_{\nu+1}^{\tau+1} \lt \frac{1}{2^{\nu+2}},
\end{equation*}as ζ is large enough. Then
 \begin{align}
2\left(M^*+2\right)s_\nu K_{\nu+1}^{\tau+1}&\leq\frac{s_{\nu-1}}{4}\left(M^*+1\right)\mu_{\nu-1}^{2\rho}K_{\nu+1}^{\tau+1}
\end{align}
\begin{align}
2\left(M^*+2\right)s_\nu K_{\nu+1}^{\tau+1}&\leq\frac{s_{\nu-1}}{4}\left(M^*+1\right)\mu_{\nu-1}^{2\rho}K_{\nu+1}^{\tau+1}
\end{align} \begin{align}
&\leq\frac{s_0}{2^{\nu+2}} \lt \frac{\gamma_0}{2^{\nu+2}} \lt \gamma_0,
\end{align}
\begin{align}
&\leq\frac{s_0}{2^{\nu+2}} \lt \frac{\gamma_0}{2^{\nu+2}} \lt \gamma_0,
\end{align} which verifies ![]() $\mathbf{(H3)}$ for all
$\mathbf{(H3)}$ for all ![]() $\nu\geq1$.
$\nu\geq1$.
Let ![]() $\zeta^{1-\rho}\geq2$ in (4.9), (4.10). We have that for all
$\zeta^{1-\rho}\geq2$ in (4.9), (4.10). We have that for all ![]() $\nu\geq1$
$\nu\geq1$
 \begin{align}
c_0\mu_\nu&\leq\frac{\mu_0}{2^\nu}\leq\frac{\mu_*^\frac{1}{2}}{2^\nu},
\end{align}
\begin{align}
c_0\mu_\nu&\leq\frac{\mu_0}{2^\nu}\leq\frac{\mu_*^\frac{1}{2}}{2^\nu},
\end{align} \begin{align}
c_0\mu_\nu\Gamma_\nu&\leq\frac{\mu_0^{1-\rho}}{2^\nu}\leq\frac{\mu_*^\frac{1}{2}}{2^\nu},
\end{align}
\begin{align}
c_0\mu_\nu\Gamma_\nu&\leq\frac{\mu_0^{1-\rho}}{2^\nu}\leq\frac{\mu_*^\frac{1}{2}}{2^\nu},
\end{align} \begin{align}
c_0s_\nu^{m-1}\mu_\nu&\leq\frac{\mu_0^{1+2\rho(m-1)}s_0^{m-1}}{2^{\nu+3}}\leq\frac{\mu_*}{2^\nu}.
\end{align}
\begin{align}
c_0s_\nu^{m-1}\mu_\nu&\leq\frac{\mu_0^{1+2\rho(m-1)}s_0^{m-1}}{2^{\nu+3}}\leq\frac{\mu_*}{2^\nu}.
\end{align} The verification of ![]() $\mathbf{(H2)}$ follows from
$\mathbf{(H2)}$ follows from ![]() $(4.15)$ and an induction application of
$(4.15)$ and an induction application of ![]() $(3.44)$ in lemma 3.6 for all
$(3.44)$ in lemma 3.6 for all ![]() $\nu=0,1,\cdots.$
$\nu=0,1,\cdots.$
Since ![]() $\left(1+\rho\right)^\eta \gt 2$, we have
$\left(1+\rho\right)^\eta \gt 2$, we have
 \begin{align*}
\frac{1}{2^{\nu+6}}\left(\left[\log\frac{1}{\mu}\right]+1\right)^\eta&\geq\frac{1}{2^{\nu+6}}\left(\left(1-\left(1+\rho\right)^\nu\right)\log\left(8^mc_0\right)-\left(1+\rho\right)^\nu\log\mu_0\right)^\eta\\
&\geq-\frac{1}{2^{\nu+6}}\left(1+\rho\right)^{\eta\nu}\left(\log\mu_0\right)^\eta\geq1.
\end{align*}
\begin{align*}
\frac{1}{2^{\nu+6}}\left(\left[\log\frac{1}{\mu}\right]+1\right)^\eta&\geq\frac{1}{2^{\nu+6}}\left(\left(1-\left(1+\rho\right)^\nu\right)\log\left(8^mc_0\right)-\left(1+\rho\right)^\nu\log\mu_0\right)^\eta\\
&\geq-\frac{1}{2^{\nu+6}}\left(1+\rho\right)^{\eta\nu}\left(\log\mu_0\right)^\eta\geq1.
\end{align*}It follows from above that
 \begin{align*}
&\log\left(n+1\right)!+\left(\nu+6\right)n\log2+3n\eta\log\left(\left[\log\frac{1}{\mu}\right]+1\right)-\frac{1}{2^{\left(\nu+6\right)}}\left(\left[\log\frac{1}{\mu}\right]+1\right)^{3\eta}\\
&\leq\log\left(n+1\right)!+\left(\nu+6\right)n\log2+3n\eta\log\left(\log\frac{1}{\mu}+2\right)-\left(\log\frac{1}{\mu}\right)^{2\eta}\\
&\leq-\log\frac{1}{\mu},
\end{align*}
\begin{align*}
&\log\left(n+1\right)!+\left(\nu+6\right)n\log2+3n\eta\log\left(\left[\log\frac{1}{\mu}\right]+1\right)-\frac{1}{2^{\left(\nu+6\right)}}\left(\left[\log\frac{1}{\mu}\right]+1\right)^{3\eta}\\
&\leq\log\left(n+1\right)!+\left(\nu+6\right)n\log2+3n\eta\log\left(\log\frac{1}{\mu}+2\right)-\left(\log\frac{1}{\mu}\right)^{2\eta}\\
&\leq-\log\frac{1}{\mu},
\end{align*}as µ is small, which is ensured by making ɛ small. Thus,
 \begin{equation*}
\int_{K_{\nu+1}}^\infty t^{n}e^{-\frac{t}{2^{\nu+6}}}dt\leq\left(n+1\right)!2^{\left(\nu+6\right)n}K_{\nu+1}^{n}e^{-\frac{K_{\nu+1}}{2^{\nu+6}}}\leq \mu,
\end{equation*}
\begin{equation*}
\int_{K_{\nu+1}}^\infty t^{n}e^{-\frac{t}{2^{\nu+6}}}dt\leq\left(n+1\right)!2^{\left(\nu+6\right)n}K_{\nu+1}^{n}e^{-\frac{K_{\nu+1}}{2^{\nu+6}}}\leq \mu,
\end{equation*} i.e. ![]() $\mathbf{(H1)}$ holds.
$\mathbf{(H1)}$ holds.
Above all, the KAM steps described in section 3 are valid for all ν, which give the desired sequences stated in the lemma.
Now, (4.1) and (4.3) follow from lemma 3.6, (4.15) and (4.17); by adding up (4.1) and (4.3) for all ![]() $\nu=0,1,\cdots$, we can get (4.2) and (4.4); (4.5) follows from (3.49) in lemma 3.9 and (4.15); (4.6) follows from (3.42) in lemma 3.6 and (4.15); (2) follows from lemma 3.8.
$\nu=0,1,\cdots$, we can get (4.2) and (4.4); (4.5) follows from (3.49) in lemma 3.9 and (4.15); (4.6) follows from (3.42) in lemma 3.6 and (4.15); (2) follows from lemma 3.8.
This completes the proof.
4.2. Convergence
The convergence is standard. For the sake of completeness, we briefly give the framework of proof. Let
By lemma 4.1, we have
 \begin{align*}
D_{\nu+1}&\subset D_\nu,\\
\Psi^\nu&:\tilde{D}_\nu\rightarrow \tilde{D}_0,\\
H_0\circ\Psi^\nu&=H_\nu=N_\nu+P_\nu,\\
N_\nu&=e_\nu+\left\langle\omega_\nu\left(\xi\right),y\right\rangle+\bar h_\nu(y,\xi),
\end{align*}
\begin{align*}
D_{\nu+1}&\subset D_\nu,\\
\Psi^\nu&:\tilde{D}_\nu\rightarrow \tilde{D}_0,\\
H_0\circ\Psi^\nu&=H_\nu=N_\nu+P_\nu,\\
N_\nu&=e_\nu+\left\langle\omega_\nu\left(\xi\right),y\right\rangle+\bar h_\nu(y,\xi),
\end{align*} ![]() $\nu=0,1,\cdots,$ where
$\nu=0,1,\cdots,$ where ![]() $\Psi^0=id$,
$\Psi^0=id$,  $\omega_\nu(\xi)=\omega_0(\xi)+\sum_{j=0}^{\nu-1}p_{01}^j\left(\xi\right)$. Using (4.7) and the identity
$\omega_\nu(\xi)=\omega_0(\xi)+\sum_{j=0}^{\nu-1}p_{01}^j\left(\xi\right)$. Using (4.7) and the identity
 \begin{align*}
\Psi^\nu=id+\sum_{i=1}^\nu\left(\Psi^i-\Psi^{i-1}\right),
\end{align*}
\begin{align*}
\Psi^\nu=id+\sum_{i=1}^\nu\left(\Psi^i-\Psi^{i-1}\right),
\end{align*} it is easy to verify that ![]() $\Psi^\nu$ is uniformly convergent and denote the limitation by
$\Psi^\nu$ is uniformly convergent and denote the limitation by ![]() $\Psi^\infty$.
$\Psi^\infty$.
In view of lemma 4.1, it is obvious to see that eν, ![]() $\bar{h}_\nu$ and ξν converge uniformly about ν, and denote its limitation by
$\bar{h}_\nu$ and ξν converge uniformly about ν, and denote its limitation by ![]() $e_\infty$,
$e_\infty$, ![]() $\bar{h}_\infty$ and
$\bar{h}_\infty$ and ![]() $\xi_\infty$. By lemma 3.5, we have
$\xi_\infty$. By lemma 3.5, we have
 \begin{align}
&\omega_1(\xi_1)=\omega_0\left(\xi_1\right)+p_{01}^0\left(\xi_1\right)=\omega_0\left(\xi_0\right),\notag\\
&\omega_2(\xi_2)=\omega_0\left(\xi_2\right)+p_{01}^0\left(\xi_2\right)+p_{01}^1\left(\xi_2\right)=\omega_0\left(\xi_0\right),\notag\\
&~~~\vdots\notag\\
&\omega_\nu(\xi_\nu)=\omega_0\left(\xi_\nu\right)+p_{01}^0\left(\xi_\nu\right)+\cdots+p_{01}^{\nu-1}\left(\xi_\nu\right)=\omega_0\left(\xi_0\right).
\end{align}
\begin{align}
&\omega_1(\xi_1)=\omega_0\left(\xi_1\right)+p_{01}^0\left(\xi_1\right)=\omega_0\left(\xi_0\right),\notag\\
&\omega_2(\xi_2)=\omega_0\left(\xi_2\right)+p_{01}^0\left(\xi_2\right)+p_{01}^1\left(\xi_2\right)=\omega_0\left(\xi_0\right),\notag\\
&~~~\vdots\notag\\
&\omega_\nu(\xi_\nu)=\omega_0\left(\xi_\nu\right)+p_{01}^0\left(\xi_\nu\right)+\cdots+p_{01}^{\nu-1}\left(\xi_\nu\right)=\omega_0\left(\xi_0\right).
\end{align}Taking limits at both sides of (4.18), we get
 \begin{align}
\omega_\infty(\xi_\infty)=\omega_0\left(\xi_\infty\right)+\sum_{j=0}^{\infty}p_{01}^j\left(\xi_\infty\right)=\omega_0(\xi_0).
\end{align}
\begin{align}
\omega_\infty(\xi_\infty)=\omega_0\left(\xi_\infty\right)+\sum_{j=0}^{\infty}p_{01}^j\left(\xi_\infty\right)=\omega_0(\xi_0).
\end{align} Then, on ![]() $D(\frac{s_0}{2})$, Nν converge uniformly to
$D(\frac{s_0}{2})$, Nν converge uniformly to
Hence, on  $D\left(\frac{s_0}{2},\frac{r_0}{2}\right)$,
$D\left(\frac{s_0}{2},\frac{r_0}{2}\right)$,
converge uniformly to
Since
 \begin{align*}
\left\vert\left\|P_\nu\right\|\right\vert_{D_\nu}\leq\gamma_0^{n+m+2}s_\nu^m\mu_\nu,
\end{align*}
\begin{align*}
\left\vert\left\|P_\nu\right\|\right\vert_{D_\nu}\leq\gamma_0^{n+m+2}s_\nu^m\mu_\nu,
\end{align*} by (4.15), we have that it converges to 0 as ![]() $\nu\rightarrow\infty$. So, on
$\nu\rightarrow\infty$. So, on ![]() $D(0,\frac{r_0}{2})$,
$D(0,\frac{r_0}{2})$,
Thus, for the given ![]() $\xi_0\in O$, the Hamiltonian
$\xi_0\in O$, the Hamiltonian
admits an analytic, quasi-periodic, invariant n-torus ![]() $\mathbb{T}^n\times\{0\}$ with the Diophantine frequency
$\mathbb{T}^n\times\{0\}$ with the Diophantine frequency ![]() $\omega(\xi_0)$, which is the corresponding unperturbed toral frequency.
$\omega(\xi_0)$, which is the corresponding unperturbed toral frequency.
Recall
 \begin{align*}\hat O& =\left\{\hat\xi_0\in O:|\omega(\hat \xi_0)-\omega(\xi_0)| \lt d,|\langle k,\omega(\hat\xi_0)\rangle|\geq\frac{\gamma}{|k|^\tau},k\in\mathbb{Z}^n\backslash\{0\}\right\},\notag\\d&=\min_{\xi\in\partial O}\left\{\;|\omega(\xi)-\omega(\xi_0)|\;\right\}.\end{align*}
\begin{align*}\hat O& =\left\{\hat\xi_0\in O:|\omega(\hat \xi_0)-\omega(\xi_0)| \lt d,|\langle k,\omega(\hat\xi_0)\rangle|\geq\frac{\gamma}{|k|^\tau},k\in\mathbb{Z}^n\backslash\{0\}\right\},\notag\\d&=\min_{\xi\in\partial O}\left\{\;|\omega(\xi)-\omega(\xi_0)|\;\right\}.\end{align*} For given ![]() $\hat\xi_0,\tilde\xi_0\in\hat O$, similar to (4.19), we obtain
$\hat\xi_0,\tilde\xi_0\in\hat O$, similar to (4.19), we obtain
 \begin{align}
\omega(\xi_\infty(\hat\xi_0))+\sum_{j=0}^{\infty}p_{01}^j(\xi_\infty(\hat\xi_0))=\omega(\hat\xi_0),
\end{align}
\begin{align}
\omega(\xi_\infty(\hat\xi_0))+\sum_{j=0}^{\infty}p_{01}^j(\xi_\infty(\hat\xi_0))=\omega(\hat\xi_0),
\end{align} \begin{align}
\omega(\xi_\infty(\tilde\xi_0))+\sum_{j=0}^{\infty}p_{01}^j(\xi_\infty(\tilde\xi_0))=\omega(\tilde\xi_0).
\end{align}
\begin{align}
\omega(\xi_\infty(\tilde\xi_0))+\sum_{j=0}^{\infty}p_{01}^j(\xi_\infty(\tilde\xi_0))=\omega(\tilde\xi_0).
\end{align} \begin{align*}
\omega(\xi_\infty(\hat\xi_0))-\omega(\xi_\infty(\tilde\xi_0))+\sum_{j=0}^{\infty}p_{01}^j(\xi_\infty(\hat\xi_0))-p_{01}^j(\xi_\infty(\tilde\xi_0))=\omega(\hat\xi_0)-\omega(\tilde\xi_0).
\end{align*}
\begin{align*}
\omega(\xi_\infty(\hat\xi_0))-\omega(\xi_\infty(\tilde\xi_0))+\sum_{j=0}^{\infty}p_{01}^j(\xi_\infty(\hat\xi_0))-p_{01}^j(\xi_\infty(\tilde\xi_0))=\omega(\hat\xi_0)-\omega(\tilde\xi_0).
\end{align*}Then
 \begin{align*}
&\left|\omega(\hat\xi_0)-\omega(\tilde\xi_0)\right|\\
&=\left|\omega(\xi_\infty(\hat\xi_0))-\omega(\xi_\infty(\tilde\xi_0))+\sum_{j=0}^{\infty}p_{01}^j(\xi_\infty(\hat\xi_0))-p_{01}^j(\xi_\infty(\tilde\xi_0))\right|\\
&\geq \left|\omega(\xi_\infty(\hat\xi_0))-\omega(\xi_\infty(\tilde\xi_0))\right|-\left|\sum_{j=0}^{\infty}p_{01}^j(\xi_\infty(\hat\xi_0))-p_{01}^j(\xi_\infty(\tilde\xi_0))\right|\\ &\geq\sigma\left\vert\xi_\infty(\hat\xi_0)-\xi_\infty(\tilde\xi_0)\right\vert^\beta-c\sum_{j=0}^{\infty}\mu_j\left\vert\xi_\infty(\hat\xi_0)-\xi_\infty(\tilde\xi_0)\right\vert^\beta\notag\\
&\geq\left(\sigma-c\sum_{j=0}^{\infty}\mu_j\right)\left\vert\xi_\infty(\hat\xi_0)-\xi_\infty(\tilde\xi_0)\right\vert^\beta\\
&\geq\frac{\sigma}{2}\left\vert\xi_\infty(\hat\xi_0)-\xi_\infty(\tilde\xi_0)\right\vert^\beta,
\end{align*}
\begin{align*}
&\left|\omega(\hat\xi_0)-\omega(\tilde\xi_0)\right|\\
&=\left|\omega(\xi_\infty(\hat\xi_0))-\omega(\xi_\infty(\tilde\xi_0))+\sum_{j=0}^{\infty}p_{01}^j(\xi_\infty(\hat\xi_0))-p_{01}^j(\xi_\infty(\tilde\xi_0))\right|\\
&\geq \left|\omega(\xi_\infty(\hat\xi_0))-\omega(\xi_\infty(\tilde\xi_0))\right|-\left|\sum_{j=0}^{\infty}p_{01}^j(\xi_\infty(\hat\xi_0))-p_{01}^j(\xi_\infty(\tilde\xi_0))\right|\\ &\geq\sigma\left\vert\xi_\infty(\hat\xi_0)-\xi_\infty(\tilde\xi_0)\right\vert^\beta-c\sum_{j=0}^{\infty}\mu_j\left\vert\xi_\infty(\hat\xi_0)-\xi_\infty(\tilde\xi_0)\right\vert^\beta\notag\\
&\geq\left(\sigma-c\sum_{j=0}^{\infty}\mu_j\right)\left\vert\xi_\infty(\hat\xi_0)-\xi_\infty(\tilde\xi_0)\right\vert^\beta\\
&\geq\frac{\sigma}{2}\left\vert\xi_\infty(\hat\xi_0)-\xi_\infty(\tilde\xi_0)\right\vert^\beta,
\end{align*}i.e.,
 \begin{align}
\left\vert\xi_\infty(\hat\xi_0)-\xi_\infty(\tilde\xi_0)\right\vert\leq\left(\frac{2}{\sigma}\right)^{\frac{1}{\beta}}\left|\omega(\hat\xi_0)-\omega(\tilde\xi_0)\right|^{\frac{1}{\beta}}.
\end{align}
\begin{align}
\left\vert\xi_\infty(\hat\xi_0)-\xi_\infty(\tilde\xi_0)\right\vert\leq\left(\frac{2}{\sigma}\right)^{\frac{1}{\beta}}\left|\omega(\hat\xi_0)-\omega(\tilde\xi_0)\right|^{\frac{1}{\beta}}.
\end{align} It follows from the Hölder continuity of ω and (4.22) that  $\xi_\infty(\hat\xi_0)$ is Hölder continuous about
$\xi_\infty(\hat\xi_0)$ is Hölder continuous about ![]() $\hat\xi_0\in \hat O$. Using the above proof process and replacing ξ 0 by
$\hat\xi_0\in \hat O$. Using the above proof process and replacing ξ 0 by ![]() $\hat\xi_0$, we can get an invariant torus with the Diophantine frequency
$\hat\xi_0$, we can get an invariant torus with the Diophantine frequency  $\omega(\hat\xi_0)$.
$\omega(\hat\xi_0)$.
5. Proof of theorem 2.5 and theorem 2.8
First, we briefly outline the proof framework of theorem 2.5 as it follows the KAM step in section 3. Here, we mainly highlight two major differences from the proof of theorem 2.1. The first difference is that we utilize homotopy invariance and excision of the topological degree to keep the frequency unchanged during the iteration process, rather than selecting parameters. This is because we consider a Hamiltonian, not a family of Hamiltonians. The second difference is that the transformation is defined on a smaller domain because we treat the action variable as a parameter, and the translation of the parameter is equivalent to the action variable’s. We need the integer ![]() $m\geq\beta+1$ to ensure that the translated action variable y does not run out of the given domain.
$m\geq\beta+1$ to ensure that the translated action variable y does not run out of the given domain.
5.1. Proof of theorem 2.5
In this section, we will describe the translation of action variable and state how the frequency can be preserved in the iterative process, which are different from subsection 3.2.6.
Let ![]() $\xi_0\in{G}$ be fixed as statement
$\xi_0\in{G}$ be fixed as statement ![]() $\mathrm{(A0)}$. The Taylor expansion of Hamiltonian (1.1) about ξ 0 reads
$\mathrm{(A0)}$. The Taylor expansion of Hamiltonian (1.1) about ξ 0 reads
where ![]() $e_0=h(\xi_0)$,
$e_0=h(\xi_0)$, ![]() $\omega_0(\xi_0)=\nabla h(\xi_0)$,
$\omega_0(\xi_0)=\nabla h(\xi_0)$,  $\bar{h}(y-\xi_0)=O(\left\vert y-\xi_0\right\vert^2)$. Using the transformation
$\bar{h}(y-\xi_0)=O(\left\vert y-\xi_0\right\vert^2)$. Using the transformation ![]() $(y-\xi_0)\rightarrow y$ in the above, we have
$(y-\xi_0)\rightarrow y$ in the above, we have
where (y, x) lies in a complex neighbourhood ![]() $D(s,r)$. Denote
$D(s,r)$. Denote
 \begin{align*}
H_0&=: H(y,x,\xi_0)=N_0+P_0,\\
N_0&=:e_0+\langle\omega_0(\xi_0),y\rangle+\bar{h}_0(y,\xi_0),\\
P_0&=:\varepsilon P(y,x,\xi_0,\varepsilon).
\end{align*}
\begin{align*}
H_0&=: H(y,x,\xi_0)=N_0+P_0,\\
N_0&=:e_0+\langle\omega_0(\xi_0),y\rangle+\bar{h}_0(y,\xi_0),\\
P_0&=:\varepsilon P(y,x,\xi_0,\varepsilon).
\end{align*} For convenience, we will omit the index for all quantities of the present KAM step (at νth step) and use + to index all quantities in the next KAM step (at ![]() $(\nu+1)$th step). Now, suppose that at νth step, we have arrived at the following real analytic Hamiltonian:
$(\nu+1)$th step). Now, suppose that at νth step, we have arrived at the following real analytic Hamiltonian:
 \begin{equation}
\begin{aligned}
H&=N+P,~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\\
N&=e+\langle\omega(\xi),y\rangle+\bar{h}(y,\xi).
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
H&=N+P,~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\\
N&=e+\langle\omega(\xi),y\rangle+\bar{h}(y,\xi).
\end{aligned}
\end{equation} First, we shall construct a symplectic transformation as the time-1 map ![]() $\phi_{F}^1$ such that it transforms the Hamiltonian H into the following form:
$\phi_{F}^1$ such that it transforms the Hamiltonian H into the following form:
The concrete details see subsection 3.2.4
Next, we will construct a translation so as to keep the frequency unchanged. Consider the translation
where ![]() $\xi_+$ is to be determined. Let
$\xi_+$ is to be determined. Let
Then
 \begin{align}
H\circ\Phi_+&=N_++P_+,\notag\\
N_+&=\bar N_+\circ\phi=e_++\langle\omega_+(\xi_+),y\rangle+\bar h_+(y,\xi_+),
\end{align}
\begin{align}
H\circ\Phi_+&=N_++P_+,\notag\\
N_+&=\bar N_+\circ\phi=e_++\langle\omega_+(\xi_+),y\rangle+\bar h_+(y,\xi_+),
\end{align}where
 \begin{align}
\bar h_+&=\bar h(y+\xi_+-\xi)-\bar h(\xi_+-\xi)-\left\langle\nabla \bar h(\xi_+-\xi),y\right\rangle
+[R](y+\xi_+-\xi)\notag\\
&~~~~-[R](\xi_+-\xi)-\left\langle\nabla[R](\xi_+-\xi),y\right\rangle.
\end{align}
\begin{align}
\bar h_+&=\bar h(y+\xi_+-\xi)-\bar h(\xi_+-\xi)-\left\langle\nabla \bar h(\xi_+-\xi),y\right\rangle
+[R](y+\xi_+-\xi)\notag\\
&~~~~-[R](\xi_+-\xi)-\left\langle\nabla[R](\xi_+-\xi),y\right\rangle.
\end{align}As in subsection 3.2.6, we will show that the frequency can be preserved in the iteration process. The following lemma is crucial to our arguments.
Lemma 5.1. There exists  $\xi_+\in B_{s\mu^{{1}/{\beta}}}(\xi)$ such that
$\xi_+\in B_{s\mu^{{1}/{\beta}}}(\xi)$ such that
Proof. The proof will be completed by an induction on ν. We begin with the case ν = 0. It is obvious that ![]() $\omega_0(\xi_0)=\omega_0(\xi_0)$. Now supposing that for some
$\omega_0(\xi_0)=\omega_0(\xi_0)$. Now supposing that for some ![]() $\nu\geq0$ we have
$\nu\geq0$ we have
 \begin{align*}
\omega_i(\xi_i)&=\omega_{i-1}(\xi_{i-1}),~~~~~\xi_i\in B_{s_{i-1}\mu_{i-1}^{{1}/{\beta}}}\left(\xi_{i-1}\right),
\end{align*}
\begin{align*}
\omega_i(\xi_i)&=\omega_{i-1}(\xi_{i-1}),~~~~~\xi_i\in B_{s_{i-1}\mu_{i-1}^{{1}/{\beta}}}\left(\xi_{i-1}\right),
\end{align*} where ![]() $i=1,2,\cdots,\nu.$ Then, we need to find
$i=1,2,\cdots,\nu.$ Then, we need to find ![]() $\xi_+$ near ξ such that
$\xi_+$ near ξ such that ![]() $\omega_+(\xi_+)=\omega(\xi)$. In view of (5.6), we observe that
$\omega_+(\xi_+)=\omega(\xi)$. In view of (5.6), we observe that
We split
Consider homotopy ![]() $H_t(y):[0,1]\times G\rightarrow \mathbb{R}^n$,
$H_t(y):[0,1]\times G\rightarrow \mathbb{R}^n$,
For any ![]() $y\in\partial G$,
$y\in\partial G$, ![]() $t\in[0,1]$, by
$t\in[0,1]$, by ![]() $\mathrm{(A1)}$, we have that
$\mathrm{(A1)}$, we have that
 \begin{align*}
\left\vert H_t(y)\right\vert&\geq\vert\omega(y)-\omega(\xi)\vert
-\vert\omega_+(y)-\omega(y)\vert\geq\vert\omega_0(y)-\omega_{0}(\xi_0)\vert-\sum_{i=0}^\nu\left\vert\omega_{i+1}(y)-\omega_i(y)\right\vert\\
&\geq\sigma\vert y-\xi_0\vert^\beta-\sum_{i=0}^{\nu}\gamma_0^{n+m+2}s_i^{m-1}\mu_i \gt \frac{\sigma\delta^\beta}{2},
\end{align*}
\begin{align*}
\left\vert H_t(y)\right\vert&\geq\vert\omega(y)-\omega(\xi)\vert
-\vert\omega_+(y)-\omega(y)\vert\geq\vert\omega_0(y)-\omega_{0}(\xi_0)\vert-\sum_{i=0}^\nu\left\vert\omega_{i+1}(y)-\omega_i(y)\right\vert\\
&\geq\sigma\vert y-\xi_0\vert^\beta-\sum_{i=0}^{\nu}\gamma_0^{n+m+2}s_i^{m-1}\mu_i \gt \frac{\sigma\delta^\beta}{2},
\end{align*} where ![]() $\delta:=\min\{\vert y-\xi_0\vert, \forall y\in\partial G\}$.
$\delta:=\min\{\vert y-\xi_0\vert, \forall y\in\partial G\}$.
So, it follows from homotopy invariance and ![]() $\mathrm{(A0)}$ that
$\mathrm{(A0)}$ that
We note by ![]() $\mathrm{(A1)}$, (5.9) and (5.10) that for any
$\mathrm{(A1)}$, (5.9) and (5.10) that for any  $y\in G\backslash B_{s\mu^{{1}/{\beta}}}(\xi)$,
$y\in G\backslash B_{s\mu^{{1}/{\beta}}}(\xi)$,
 \begin{align}
\left\vert H_1(y)\right\vert&=\vert\omega_+(y)-\omega(\xi)\vert\geq \vert y-\xi\vert^\beta-c_1\gamma_0^{n+m+2}s^{m-1}\mu\notag\\
&\geq s^\beta \mu-c_1\gamma_0^{n+m+2}s^{m-1}\mu\geq\frac{s^\beta\mu}{2},
\end{align}
\begin{align}
\left\vert H_1(y)\right\vert&=\vert\omega_+(y)-\omega(\xi)\vert\geq \vert y-\xi\vert^\beta-c_1\gamma_0^{n+m+2}s^{m-1}\mu\notag\\
&\geq s^\beta \mu-c_1\gamma_0^{n+m+2}s^{m-1}\mu\geq\frac{s^\beta\mu}{2},
\end{align} where the last equality follows from ![]() $m\geq \beta+1$.
$m\geq \beta+1$.
Hence, by excision, we have that
 \begin{align*}
\deg\left(H_1(\cdot),B_{s\mu^{{1}/{\beta}}}(\xi),0\right)=\deg\left(H_1(\cdot),G^o,0\right)\neq0,
\end{align*}
\begin{align*}
\deg\left(H_1(\cdot),B_{s\mu^{{1}/{\beta}}}(\xi),0\right)=\deg\left(H_1(\cdot),G^o,0\right)\neq0,
\end{align*} i.e., there exists at least a  $\xi_+\in B_{s\mu^{{1}/{\beta}}}(\xi)$, such that
$\xi_+\in B_{s\mu^{{1}/{\beta}}}(\xi)$, such that ![]() $H_1(\xi_+)=0,$ i.e.,
$H_1(\xi_+)=0,$ i.e.,
which implies (5.8).
This completes the proof.
In the following, we prove
 \begin{align}
\phi:D_{\frac{1}{8}\alpha}\rightarrow D_{\frac{1}{4}\alpha}.
\end{align}
\begin{align}
\phi:D_{\frac{1}{8}\alpha}\rightarrow D_{\frac{1}{4}\alpha}.
\end{align} Recall that ![]() $m\geq\beta+1$ and
$m\geq\beta+1$ and  $\alpha=\mu^{\frac{1}{m+1}}$, we have
$\alpha=\mu^{\frac{1}{m+1}}$, we have
 \begin{align}
cs\mu^{\frac{1}{\beta}} \lt \frac{1}{8}\alpha s.
\end{align}
\begin{align}
cs\mu^{\frac{1}{\beta}} \lt \frac{1}{8}\alpha s.
\end{align} For  $\forall (y,x)\in D_{\frac{1}{8}\alpha}$, we note by
$\forall (y,x)\in D_{\frac{1}{8}\alpha}$, we note by  $\xi_+\in B_{s\mu^{{1}/{\beta}}}(\xi)$ in lemma 5.1 and (5.13) that
$\xi_+\in B_{s\mu^{{1}/{\beta}}}(\xi)$ in lemma 5.1 and (5.13) that
 \begin{equation*}\left\vert y+\xi_+-\xi\right\vert \lt \vert y\vert+\vert \xi_+-\xi\vert \lt \frac{1}{8}\alpha s+cs\mu^{\frac{1}{\beta}} \lt \frac{1}{4}\alpha s,\end{equation*}
\begin{equation*}\left\vert y+\xi_+-\xi\right\vert \lt \vert y\vert+\vert \xi_+-\xi\vert \lt \frac{1}{8}\alpha s+cs\mu^{\frac{1}{\beta}} \lt \frac{1}{4}\alpha s,\end{equation*}which implies (5.12).
Next, we prove theorem 2.8 by a direct method.
5.2. Proof of theorem 2.8
(1) The unperturbed motion of (1.1) is described by the equation
 \begin{equation*}
\left\{
\begin{array}{ll}
\dot{y}=0,\\
\dot{x}= h'(y).
\end{array}
\right.
\end{equation*}
\begin{equation*}
\left\{
\begin{array}{ll}
\dot{y}=0,\\
\dot{x}= h'(y).
\end{array}
\right.
\end{equation*} The flow is ![]() $x=h'(y)t+x_0,y\in G$, where x 0 is an initial condition. Notice that
$x=h'(y)t+x_0,y\in G$, where x 0 is an initial condition. Notice that
i.e., h(y) is degenerate at ![]() $\xi_0=0$. Obviously, by simple calculation, we get
$\xi_0=0$. Obviously, by simple calculation, we get
i.e., ![]() $\mathrm{(A0)}$ fails, then theorem 2.6 is not applicable.
$\mathrm{(A0)}$ fails, then theorem 2.6 is not applicable.
Note that the perturbed motion equation is
 \begin{equation*}
\left\{
\begin{array}{ll}
\dot{y}=0,\\
\dot{x}=h'(y)+\varepsilon P'(y).
\end{array}
\right.
\end{equation*}
\begin{equation*}
\left\{
\begin{array}{ll}
\dot{y}=0,\\
\dot{x}=h'(y)+\varepsilon P'(y).
\end{array}
\right.
\end{equation*} The flow is ![]() $x=\left(h'(y)+\varepsilon P'(y)\right)t+x_1,~y\in G$, where x 1 is an initial condition. To ensure the frequency is equal to
$x=\left(h'(y)+\varepsilon P'(y)\right)t+x_1,~y\in G$, where x 1 is an initial condition. To ensure the frequency is equal to ![]() $h'(0)$, we need to find a solution of the following equation in G:
$h'(0)$, we need to find a solution of the following equation in G:
i.e.,
Notice that the Taylor expansion of ![]() $g'(y)$ at
$g'(y)$ at ![]() $\xi_0=0$ is
$\xi_0=0$ is
then the equation (5.14) is equivalent to
which is solvable provided that ![]() $\varepsilon P'(y)\, sign \left(g^{2\ell+1}(0)\right) \lt 0$. So the perturbed system admits at least two invariant tori with frequency
$\varepsilon P'(y)\, sign \left(g^{2\ell+1}(0)\right) \lt 0$. So the perturbed system admits at least two invariant tori with frequency ![]() $\omega=h'(0)$ for the small enough perturbation satisfying
$\omega=h'(0)$ for the small enough perturbation satisfying ![]() $\varepsilon P'(y)\, sign \left(g^{2\ell+1}(0)\right) \lt 0$. Conversely, if
$\varepsilon P'(y)\, sign \left(g^{2\ell+1}(0)\right) \lt 0$. Conversely, if ![]() $\varepsilon P'(y)\, sign \left(g^{2\ell+1}(0)\right) \gt 0$, the unperturbed invariant torus with frequency
$\varepsilon P'(y)\, sign \left(g^{2\ell+1}(0)\right) \gt 0$, the unperturbed invariant torus with frequency ![]() $\omega=h'(0)$ will be destroyed.
$\omega=h'(0)$ will be destroyed.
(2) Note that h(y) is degenerate in ![]() $\xi_0=0$. Obviously, by simple calculation, we get
$\xi_0=0$. Obviously, by simple calculation, we get
Then, by theorem 2.6, the above persistence result hold. In addition, we can also directly prove this result. Similarly, we need to solve the following equation in G:
i.e.,
Notice that the Taylor expansion of ![]() $g'(y)$ at
$g'(y)$ at ![]() $\xi_0=0$ is
$\xi_0=0$ is
 \begin{equation*}g'(y)=g'(0)+g''(0)y+\cdots+g^{2\ell+2}(0)y^{2\ell+1}+o\left(y^{2\ell+1}\right),\end{equation*}
\begin{equation*}g'(y)=g'(0)+g''(0)y+\cdots+g^{2\ell+2}(0)y^{2\ell+1}+o\left(y^{2\ell+1}\right),\end{equation*}then the equation (5.15) is equivalent to
 \begin{equation*}g^{2\ell+2}\left(0\right)y^{2\ell+1}+o\left(y^{2\ell+1}\right)=-\varepsilon P'(y),\end{equation*}
\begin{equation*}g^{2\ell+2}\left(0\right)y^{2\ell+1}+o\left(y^{2\ell+1}\right)=-\varepsilon P'(y),\end{equation*} whose solution always exists in G for any small enough perturbation. Hence, the perturbed system admits an invariant torus with frequency ![]() $\omega=h'(0)$ for any small enough perturbation.
$\omega=h'(0)$ for any small enough perturbation.
Acknowledgements
The authors would like to thank the editors and referees for their valuable suggestions and comments. The first author (Jiayin Du) is supported by the Fundamental Research Funds for the Central Universities (Grant number 2412024QD003). The second author (Yong Li) is supported by National Basic Research Program of China (Grant number 2013CB8-34100), National Natural Science Foundation of China (Grant numbers 11571065, 11171132, and 12071175), and Natural Science Foundation of Jilin Province (Grant number 20200201253JC).
Appendix A. Proof of proposition 2.3
Proof. Obviously, for ![]() $\forall \xi\in (-1,1)\times(-1,1)$,
$\forall \xi\in (-1,1)\times(-1,1)$,
and for ![]() $\forall \xi\in\partial(-1,1)\times(-1,1),$
$\forall \xi\in\partial(-1,1)\times(-1,1),$
Using Borsuk’s theorem in [Reference Motreanu, Motreanu and Papageorgiou27], we have
i.e.,
i.e., ![]() $\mathrm{(A0)}$ holds. For
$\mathrm{(A0)}$ holds. For  $\xi,\xi_*\in\left[-\frac{1}{2},\frac{1}{2}\right]$, and
$\xi,\xi_*\in\left[-\frac{1}{2},\frac{1}{2}\right]$, and ![]() $\xi\neq\xi_*$, we have
$\xi\neq\xi_*$, we have
but
 \begin{equation*}\left\vert\xi-\xi_*\right\vert^L \gt 0,~~\forall L \gt 0,\end{equation*}
\begin{equation*}\left\vert\xi-\xi_*\right\vert^L \gt 0,~~\forall L \gt 0,\end{equation*} which shows that ![]() $\mathrm{(A1)}$ fails. Note that the flow of unperturbed motion equation is
$\mathrm{(A1)}$ fails. Note that the flow of unperturbed motion equation is
where x 0 is an initial condition, and the flow of perturbed motion equation is
 \begin{equation*}x=\left(\omega(\xi)+\left(0,P_0\left(\varepsilon\right)\right)^\top\right)t+x_0,~~~\xi\in (-1,1)\times(-1,1).\end{equation*}
\begin{equation*}x=\left(\omega(\xi)+\left(0,P_0\left(\varepsilon\right)\right)^\top\right)t+x_0,~~~\xi\in (-1,1)\times(-1,1).\end{equation*} In order to keep the frequency ![]() $\omega(0)=\bar\omega$ unchanged, we have to solve the following equation
$\omega(0)=\bar\omega$ unchanged, we have to solve the following equation
 \begin{equation*}\omega(\xi)+\left(0,P_0\left(\varepsilon\right)\right)^\top=\bar\omega,\end{equation*}
\begin{equation*}\omega(\xi)+\left(0,P_0\left(\varepsilon\right)\right)^\top=\bar\omega,\end{equation*}i.e.
 \begin{equation*}\omega\left(\xi\right)-\bar\omega\left(\xi\right)=\left(\xi_1, \omega_2-\bar\omega_2\right)^\top=-\left(0,P_0\left(\varepsilon\right)\right)^\top,\end{equation*}
\begin{equation*}\omega\left(\xi\right)-\bar\omega\left(\xi\right)=\left(\xi_1, \omega_2-\bar\omega_2\right)^\top=-\left(0,P_0\left(\varepsilon\right)\right)^\top,\end{equation*} which implies that the second component ξ 2 of solution ξ is discontinuous and alternately appears on  $\left(-1,-\frac{1}{2}\right)$ and
$\left(-1,-\frac{1}{2}\right)$ and  $\left(\frac{1}{2},1\right)$ as
$\left(\frac{1}{2},1\right)$ as ![]() $\varepsilon\rightarrow0_+$. Hence we cannot find a solution ξɛ such that
$\varepsilon\rightarrow0_+$. Hence we cannot find a solution ξɛ such that ![]() $\xi_\varepsilon\rightarrow\xi_0$ as
$\xi_\varepsilon\rightarrow\xi_0$ as ![]() $\varepsilon\rightarrow0$.
$\varepsilon\rightarrow0$.
Appendix B. Proof of theorem 2.6
Proof. Notice that
For ![]() $0 \lt \delta \lt 1$,
$0 \lt \delta \lt 1$, ![]() $B_\delta(0)$ denotes the open ball centred at the origin with radius δ. We have that
$B_\delta(0)$ denotes the open ball centred at the origin with radius δ. We have that ![]() $\nabla h(y)-\nabla h(0)$ is odd and unequal to zero on
$\nabla h(y)-\nabla h(0)$ is odd and unequal to zero on ![]() $\partial B_\delta(0)$, i.e.,
$\partial B_\delta(0)$, i.e.,
It follows from Borsuk’s theorem in [Reference Motreanu, Motreanu and Papageorgiou27] that,
Obviously, there exist  $\sigma=\frac{\min_{y\in B_\delta(0)}\{{(y+\varrho)\vert y+\varrho\vert^{2\ell}-y\vert y\vert^{2\ell}}\}}{2\varrho^{2\ell+1}}$ and
$\sigma=\frac{\min_{y\in B_\delta(0)}\{{(y+\varrho)\vert y+\varrho\vert^{2\ell}-y\vert y\vert^{2\ell}}\}}{2\varrho^{2\ell+1}}$ and ![]() $L=2l+1$ such that
$L=2l+1$ such that
 \begin{align*}
\left\vert\nabla h(y)-\nabla h(y_*)\right\vert\geq\sigma\left\vert y-y_*\right\vert^L,~~y_*\in B_\delta(0), y\in B_\delta(0)\setminus B_\varrho(y_*),
\end{align*}
\begin{align*}
\left\vert\nabla h(y)-\nabla h(y_*)\right\vert\geq\sigma\left\vert y-y_*\right\vert^L,~~y_*\in B_\delta(0), y\in B_\delta(0)\setminus B_\varrho(y_*),
\end{align*} where ϱ > 0, ![]() $B_\varrho(y_*)\subset B_\delta(0)$. So, by theorem 2.5, the perturbed system admits an invariant torus with frequency ω for any small enough perturbation.
$B_\varrho(y_*)\subset B_\delta(0)$. So, by theorem 2.5, the perturbed system admits an invariant torus with frequency ω for any small enough perturbation.
Appendix C. Proof of proposition 2.7
Proof. Let ![]() $\varepsilon P=\varepsilon y, \varepsilon \gt 0$. Notice that for
$\varepsilon P=\varepsilon y, \varepsilon \gt 0$. Notice that for ![]() $y\in G\subset\mathbb{R}^1$,
$y\in G\subset\mathbb{R}^1$,
 \begin{equation*}h'(y)=\omega+y^{2\ell},~~h'(0)=\omega,~~h''(y)\big\vert_{y=0}=0,\end{equation*}
\begin{equation*}h'(y)=\omega+y^{2\ell},~~h'(0)=\omega,~~h''(y)\big\vert_{y=0}=0,\end{equation*} which implies that the Hamiltonian H is degenerate at y = 0. By the definition of degree, we have for ![]() $0 \lt \delta \lt 1$
$0 \lt \delta \lt 1$
i.e., ![]() $\mathrm{(A0)}$ fails. Then, theorem 2.5 cannot be used to prove the persistence result of keeping frequency unchanged.
$\mathrm{(A0)}$ fails. Then, theorem 2.5 cannot be used to prove the persistence result of keeping frequency unchanged.
Note that the flow of unperturbed motion equation at y = 0 is
where x 0 is an initial condition, and the flow of perturbed motion equation is
 \begin{equation*}x=\left(\omega+y^{2\ell}+\varepsilon\right)t+x_0,~~~y\in G.\end{equation*}
\begin{equation*}x=\left(\omega+y^{2\ell}+\varepsilon\right)t+x_0,~~~y\in G.\end{equation*} In order to preserve frequency ω, we need to solve ![]() $y^{2\ell}+\varepsilon=0$ in G, which has no real solution in G. Hence, the persistence result of keeping frequency unchanged fails.
$y^{2\ell}+\varepsilon=0$ in G, which has no real solution in G. Hence, the persistence result of keeping frequency unchanged fails.