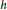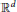This paper studies the uncertainty principle for spherical $h$ -harmonic expansions on the unit sphere of ${{\mathbb{R}}^{d}}$ associated with a weight function invariant under a general finite reflection group, which is in full analogy with the classical Heisenberg inequality. Our proof is motivated by a new decomposition of the Dunkl–Laplace–Beltrami operator on the weighted sphere.