Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-23T11:08:03.387Z Has data issue: false hasContentIssue false
  • English
  • Français

Uncertainty Principles on Weighted Spheres, Balls, and Simplexes

Published online by Cambridge University Press:  20 November 2018

Han Feng
Han Feng*
Affiliation:
Department of Mathematical and Statistical Sciences, University of Alberta, Edmonton, AB T@G zGË e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper studies the uncertainty principle for spherical 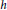$h$ -harmonic expansions on the unit sphere of 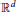${{\mathbb{R}}^{d}}$ associated with a weight function invariant under a general finite reflection group, which is in full analogy with the classical Heisenberg inequality. Our proof is motivated by a new decomposition of the Dunkl–Laplace–Beltrami operator on the weighted sphere.

Keywords

42C1042B10uncertainty principleDunkl theory
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 59 , Issue 1 , 01 March 2016 , pp. 62 - 72
Copyright
Copyright © Canadian Mathematical Society 2016

References

[1] Dai, F. and Feng, H.. Riesz transforms and fractional integration for orthogonal expansions on spheres, balls and simplices. Preprint, 2014.Google Scholar
[2] Dai, F. and Wang, H.. A transference theorem for the Dunkl transform and its applications. J. Funct. Anal. 258(2010), no. 12, 4052–4074. http://dx.doi.Org/10.101 6/j.jfa.2O1 0.03.006 Google Scholar
[3] Dai, F. and Xu, Y.. The Hardy-Rellich inequality and uncertainty principle on the sphere. Constr. Approx. 40(2014), no. 1, 141–171. http://dx.doi.Org/10.1007/s00365-014-9235-5 Google Scholar
[4] Dai, F. and Xu, Y.. Approximation theory and harmonic analysis on spheres and balls. Springer Monographs in Mathematics, Springer, New York, 2013.Google Scholar
[5] Dunkl, C. F., Reflection groups and orthogonal polynomials on the sphere. Math. Z. 197(1988), 33–60. http://dx.doi.Org/10.1007/BF01161629 Google Scholar
[6] Dunkl, C. F., Differential-difference operators associated to reflection groups. Trans. Amer. Math. Soc. 311(1989), no. 1, 167–183. http://dx.doi.Org/10.1090/S0002-9947-1989-0951883-8 Google Scholar
[7] Dunkl, C. F., Integral kernels with reflection group invariance. Canad. J. Math. 43(1991), no. 6, 1213–1227. http://dx.doi.Org/10.4153/CJM-1991-069-8 Google Scholar
[8] Dunkl, C. F. and Xu, Y.. Orthogonal polynomials of several variables. Second éd., Encyclopedia of Mathematics and its Applications, 155, Cambridge University Press, Cambridge, 2014. http://dx.doi.Org/10.101 7/CBO9781107786134 Google Scholar
[9] Folland, G. B. and Sitaram, A.. The uncertainty principle: a mathematical survey. J. Fourier Anal. Appl. 3(1997), no. 3, 207–238 . http://dx.doi.Org/10.1007/BF02649110 Google Scholar
[10] Rosier, M. and Voit, M.. An uncertainty principle for ultraspherical expansions. J. Math. Anal. Appl. 209(1997), no. 2, 624–634 . http://dx.doi.Org/10.1006/jmaa.1 997.5386 Google Scholar
[11] Xu, Y., Uncertainty principle on weighted spheres, balls and simplexes. J. Approx. Theory 192(2015), 193–214. http://dx.doi.Org/! 0.101 6/j.jat.2O14.11.003 Google Scholar