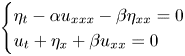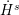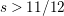4 results
On the linearized Whitham–Broer–Kaup system on bounded domains
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 07 September 2023, pp. 1-20
-
- Article
- Export citation
Estimates for evolutionary partial differential equations in classical function spaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 01 September 2023, e76
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GLOBAL ATTRACTOR FOR WEAKLY DAMPED, FORCED mKdV EQUATION BELOW ENERGY SPACE
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 241 / March 2021
- Published online by Cambridge University Press:
- 20 June 2019, pp. 171-203
- Print publication:
- March 2021
-
- Article
- Export citation
Quantum Ergodicity of Boundary Values of Eigenfunctions: A Control Theory Approach
-
- Journal:
- Canadian Mathematical Bulletin / Volume 48 / Issue 1 / 01 March 2005
- Published online by Cambridge University Press:
- 20 November 2018, pp. 3-15
- Print publication:
- 01 March 2005
-
- Article
-
- You have access
- Export citation