Hostname: page-component-745bb68f8f-kw2vx Total loading time: 0 Render date: 2025-02-11T05:49:12.887Z Has data issue: false hasContentIssue false
  • English
  • Français

On the linearized Whitham–Broer–Kaup system on bounded domains

Part of: Infinite-dimensional dissipative dynamical systems Partial differential equations Spectral theory and eigenvalue problems General higher-order equations and systems

Published online by Cambridge University Press:  07 September 2023

L. Liverani ,
Y. Mammeri ,
V. Pata  and
R. Quintanilla Open the ORCID record for R. Quintanilla [Opens in a new window]
L. Liverani
Affiliation:
Dipartimento di Matematica e Applicazioni Università di Milano Bicocca, Edificio U5, Via Cozzi 55, Milano, 20125 Italy ([email protected])
Y. Mammeri
Affiliation:
Université Jean Monnet - Institut Camille Jordan CNRS UMR 5208, 23 Rue du Dr Paul Michelon, Saint-Etienne, 42100 France ([email protected])
V. Pata
Affiliation:
Politecnico di Milano - Dipartimento di Matematica, Piazza Leonardo da Vinci, 32, Milano, 20133 Italy ([email protected])
R. Quintanilla
Affiliation:
Departament de Matemàtiques, Universitat Politècnica de Catalunya, C. Colom 11, Terrassa, 08222 Barcelona, Spain ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the system of partial differential equations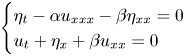

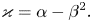
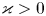\[ \begin{cases} \eta_t - \alpha u_{xxx} - \beta \eta_{xx} = 0 \\ u_t + \eta_x + \beta u_{xx} = 0 \end{cases} \]
on bounded domains, known in the literature as the Whitham–Broer–Kaup system. The well-posedness of the problem, under suitable boundary conditions, is addressed, and it is shown to depend on the sign of the number
\[ \varkappa=\alpha-\beta^2. \]
In particular, existence and uniqueness occur if and only if $\varkappa >0$. In which case, an explicit representation for the solutions is given. Nonetheless, for the case $\varkappa \leq 0$ 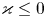we have uniqueness in the class of strong solutions, and sufficient conditions to guarantee exponential instability are provided.

Keywords

Whitham–Broer–Kaup systemdispersive equationsspectrumlinear semigroups

MSC classification

Primary: 35A01: Existence problems
Secondary: 35G16: Initial-boundary value problems for linear higher-order equations 35P10: Completeness of eigenfunctions, eigenfunction expansions 37L50: Noncompact semigroups; dispersive equations; perturbations of Hamiltonian systems
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , First View , pp. 1 - 20
Check for updates
Copyright
Copyright © The Author(s), 2023. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ames, K. A. and Straughan, B.. Non-standard and improperly posed problems (Academic Press, San Diego, 1997).Google Scholar
Anber, A. and Dahmani, Z.. The fractional Whitham–Broer–Kaup equations solved by the VIM method. J. Adv. Res. Sci. Comput. 2 (2010), 35–45.Google Scholar
Asgari, Z., Dehghan, M. and Mohebbi, A.. Numerical solution of nonlinear Jaulent-Miodek and Whitham–Broer–Kaup equations. Commun. Nonlinear Sci. Numer. Simul. 17 (2012), 4602–4610.Google Scholar
Atangana, A. and Baleanu, D., Nonlinear fractional Jaulent-Miodek and Whitham–Broer–Kaup equations within Sumudu transform. Abstr. Appl. Anal. 2013 (2013), 160681.CrossRefGoogle Scholar
Bedjaoui, N., Kumar, R. and Mammeri, Y.. Asymptotic behavior of solution of Whitham–Broer–Kaup type equations with negative dispersion. J. Appl. Anal. 28 (2022), 109–119.CrossRefGoogle Scholar
Bedjaoui, N. and Mammeri, Y., Well-posedness of Whitham–Broer–Kaup equation with negative dispersion, Preprint.Google Scholar
Broer, L. J. F.. Approximate equations for long water waves. Appl. Sci. Res. 31 (1975), 377–395.CrossRefGoogle Scholar
Chen, X. and Wang, L.. Approximate analytical solutions of time fractional Whitham–Broer–Kaup equations by a residual power series method. Entropy 17 (2015), 6519–6533.Google Scholar
Daniali, H. and Rafei, M.. Application of the variational iteration method to the Whitham–Broer–Kaup equations. Comput. Math. Appl. 54 (2007), 1079–1085.Google Scholar
Engel, K.-J. and Nagel, R.. One-parameter semigroups for linear evolution equations (Springer-Verlag, New York, 2000).Google Scholar
Kato, T.. Perturbation theory for linear operators, Springer-Verlag (Springer-Verlag, New York, 1980).Google Scholar
Kaup, D. J.. A higher-order water-wave equation and the method for solving it. Prog. Theor. Phys. 54 (1975), 396–408.CrossRefGoogle Scholar
Kupershmidt, B. A.. Mathematics of dispersive water waves. Commun. Math. Phys. 99 (1985), 51–73.CrossRefGoogle Scholar
Li, Z. and Xu, G.. Exact travelling wave solutions of the Whitham–Broer–Kaup and Broer–Kaup–Kupershmidt equations. Chaos Solitons Fractals 24 (2005), 549–556.Google Scholar
Pazy, A.. Semigroups of linear operators and applications to partial differential equations (Springer-Verlag, New York, 1983).CrossRefGoogle Scholar
Rogers, C. and Pashaev, O.. On a 2+1-dimensional Whitham–Broer–Kaup system: a resonant NLS connection. Stud. Appl. Math. 127 (2011), 141–152.CrossRefGoogle Scholar
Rudin, W.. Functional analysis (McGraw-Hill, New York-Düsseldorf-Johannesburg, 1973).Google Scholar
Whitham, G. B.. Variational methods and applications to water waves. Proc. R. Soc. A 299 (1967), 6–25.Google Scholar
Xie, F., Yan, Z. and Zhang, H.. Explicit and exact traveling wave solutions of Whitham–Broer–Kaup shallow water equations. Phys. Lett. A 285 (2001), 76–80.CrossRefGoogle Scholar
Xu, T., Liu, C., Qi, F., Li, C. and Meng, D.. New double Wronskian solutions of the Whitham–Broer–Kaup system: asymptotic analysis and resonant soliton interactions. J. Nonlinear Math. Phys. 24 (2017), 116–141.CrossRefGoogle Scholar
Yan, Z. and Zhang, H.. New explicit solitary wave solutions and periodic wave solutions for Whitham–Broer–Kaup equation in shallow water. Phys. Lett. A 285 (2001), 355–362.CrossRefGoogle Scholar