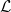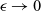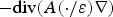26 results
EMBED IN ENSEMBLE TO RIGOROUSLY AND ACCURATELY HOMOGENIZE QUASI-PERIODIC MULTI-SCALE HETEROGENEOUS MATERIAL
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 19 September 2024, pp. 1-34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Modelling of the fluid flow in a thin domain with injection through permeable boundary
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 35 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 25 April 2024, pp. 776-796
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dynamics and steady state of squirmer motion in liquid crystal
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 35 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 10 July 2023, pp. 225-266
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Homogenization of non-symmetric jump processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 05 June 2023, pp. 1-33
- Print publication:
- March 2024
-
- Article
-
- You have access
- HTML
- Export citation
A homogenised model for the motion of evaporating fronts in porous media
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 23 January 2023, pp. 806-837
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dirichlet vs Neumann
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 4 / November 2022
- Published online by Cambridge University Press:
- 22 November 2022, pp. 1063-1074
-
- Article
- Export citation
Homogenisation of a two-phase problem with nonlinear dynamic Wentzell-interface condition for connected–disconnected porous media
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 21 June 2022, pp. 617-641
-
- Article
- Export citation
Charge transport modelling of Lithium-ion batteries
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 6 / December 2022
- Published online by Cambridge University Press:
- 21 October 2021, pp. 983-1031
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Geometric series expansion of the Neumann–Poincaré operator: Application to composite materials
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 11 May 2021, pp. 560-585
-
- Article
- Export citation
Modelling viscoelastic wave phenomenon by homogenisation of the poroelasticity equations
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 5 / October 2021
- Published online by Cambridge University Press:
- 18 January 2021, pp. 846-864
-
- Article
- Export citation
Homogenisation applied to thermal radiation in porous media
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 5 / October 2021
- Published online by Cambridge University Press:
- 03 December 2020, pp. 784-805
-
- Article
- Export citation
Bloch wave homogenisation of quasiperiodic media
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 05 October 2020, pp. 58-78
-
- Article
- Export citation
Existence and two-scale convergence of the generalised Poisson–Nernst–Planck problem with non-linear interface conditions
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 03 August 2020, pp. 683-710
-
- Article
-
- You have access
- Open access
- Export citation
Homogenisation problems in reactive decontamination
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 30 September 2019, pp. 782-805
-
- Article
- Export citation
Cauchy problem and periodic homogenization for nonlocal Hamilton–Jacobi equations with coercive gradient terms
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 17 September 2019, pp. 3028-3059
- Print publication:
- December 2020
-
- Article
- Export citation
First-order expansions for eigenvalues and eigenfunctions in periodic homogenization
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 20 March 2019, pp. 2189-2215
- Print publication:
- October 2020
-
- Article
- Export citation
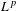 $L^{p}$ ESTIMATES FOR THE HOMOGENIZATION OF STOKES PROBLEM IN A PERFORATED DOMAIN
$L^{p}$ ESTIMATES FOR THE HOMOGENIZATION OF STOKES PROBLEM IN A PERFORATED DOMAIN
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 10 April 2018, pp. 231-258
- Print publication:
- January 2020
-
- Article
- Export citation
Computing Residual Diffusivity by Adaptive Basis Learning via Spectral Method
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 10 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 09 May 2017, pp. 351-372
- Print publication:
- May 2017
-
- Article
- Export citation
Second-Order Two-Scale Analysis Method for the Heat Conductive Problem with Radiation Boundary Condition in Periodical Porous Domain
-
- Journal:
- Communications in Computational Physics / Volume 14 / Issue 4 / October 2013
- Published online by Cambridge University Press:
- 03 June 2015, pp. 1027-1057
- Print publication:
- October 2013
-
- Article
- Export citation
An Efficient Numerical Model for Immiscible Two-Phase Flow in Fractured Karst Reservoirs
-
- Journal:
- Communications in Computational Physics / Volume 13 / Issue 2 / February 2013
- Published online by Cambridge University Press:
- 03 June 2015, pp. 540-558
- Print publication:
- February 2013
-
- Article
- Export citation