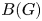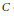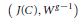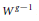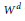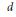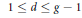9 results
Tropical curves in abelian surfaces I: enumeration of curves passing through points
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 177 / Issue 1 / July 2024
- Published online by Cambridge University Press:
- 19 September 2024, pp. 109-148
- Print publication:
- July 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sums of squares, Hankel index and almost real rank
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 30 May 2024, e70
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Interpolation for Brill–Noether curves
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 11 October 2023, e25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Floor diagrams and enumerative invariants of line bundles over an elliptic curve
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 8 / August 2023
- Published online by Cambridge University Press:
- 07 July 2023, pp. 1741-1790
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
G-torseurs en théorie de Hodge p-adique
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 10 / October 2020
- Published online by Cambridge University Press:
- 24 November 2020, pp. 2076-2110
- Print publication:
- October 2020
-
- Article
- Export citation
Erratum: Linear Projections and Successive Minima
-
- Journal:
- Nagoya Mathematical Journal / Volume 216 / 2014
- Published online by Cambridge University Press:
- 11 January 2016, pp. 111-115
- Print publication:
- 2014
-
- Article
-
- You have access
- Export citation
Linear projections and successive minima
-
- Journal:
- Nagoya Mathematical Journal / Volume 197 / March 2010
- Published online by Cambridge University Press:
- 11 January 2016, pp. 45-57
- Print publication:
- March 2010
-
- Article
-
- You have access
- Export citation
green's canonical syzygy conjecture for generic curves of odd genus
-
- Journal:
- Compositio Mathematica / Volume 141 / Issue 5 / September 2005
- Published online by Cambridge University Press:
- 01 September 2005, pp. 1163-1190
- Print publication:
- September 2005
-
- Article
-
- You have access
- Export citation
A Generalized Torelli Theorem
-
- Journal:
- Canadian Journal of Mathematics / Volume 55 / Issue 2 / 01 April 2003
- Published online by Cambridge University Press:
- 20 November 2018, pp. 248-265
- Print publication:
- 01 April 2003
-
- Article
-
- You have access
- Export citation