Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-22T09:56:51.306Z Has data issue: false hasContentIssue false
  • English
  • Français

G-torseurs en théorie de Hodge p-adique

Part of: Algebraic groups Curves Algebraic number theory: local and $p$-adic fields

Published online by Cambridge University Press:  24 November 2020

Laurent Fargues
Laurent Fargues*
Affiliation:
CNRS, Institut de Mathématiques de Jussieu, 4 place Jussieu, 75252Paris, [email protected]
Get access Rights & Permissions [Opens in a new window]

Résumé

Étant donné un groupe réductif 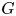$G$ sur une extension de degré fini de 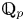$\mathbb {Q}_p$ on classifie les 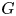$G$-fibrés sur la courbe introduite dans Fargues and Fontaine [Courbes et fibrés vectoriels en théorie de Hodge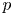$p$-adique, Astérisque 406 (2018)]. Le résultat est interprété en termes de l'ensemble 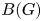$B(G)$ de Kottwitz. On calcule également la cohomologie étale de la courbe à coefficients de torsion en lien avec la théorie du corps de classe local.

Abstract

Abstract

Given a reductive group 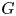$G$ over a finite extension of 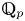$\mathbb {Q}_p$ we classify the 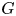$G$-bundles over the curve introduced in Fargues and Fontaine [Courbes et fibrés vectoriels en théorie de Hodge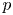$p$-adique, Astérisque 406 (2018)]. The result is interpreted in terms of Kottwitz set 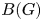$B(G)$. We moreover compute the étale cohomology of the curve with torsion coefficients and relate the result to local class field theory.

Keywords

p-adic Hodge theoryreduction theoryprincipal G-bundles

MSC classification

Primary: 11S31: Class field theory; $p$-adic formal groups 14H99: None of the above, but in this section 14L05: Formal groups, $p$-divisible groups 14L24: Geometric invariant theory
Type
Research Article
Information
Compositio Mathematica , Volume 156 , Issue 10 , October 2020 , pp. 2076 - 2110
Check for updates
Copyright
© The Author(s) 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

L'auteur a bénéficié du support du projet ANR-14-CE25 ‘PerCoLaTor’.

References

Atiyah, M. F. and Bott, R., The Yang-Mills equations over Riemann surfaces, Philos. Trans. Roy. Soc. A 308 (1983), 523–615.Google Scholar
Behrend, K. A., Semi-stability of reductive group schemes over curves, Math. Ann. 301 (1995), 281–305.CrossRefGoogle Scholar
Biswas, I. and Holla, Y. I., Harder-Narasimhan reduction of a principal bundle, Nagoya Math. J. 174 (2004), 201–223.CrossRefGoogle Scholar
Borovoi, M., Abelian Galois cohomology of reductive groups, Mem. Amer. Math. Soc. 132 (626) (1998).Google Scholar
Cornut, C., Filtrations and buildings, Mem. Amer. Math. Soc., to appear.Google Scholar
Dat, J.-F., Orlik, S. and Rapoport, M., Period domains over finite and p-adic fields, Cambridge Tracts in Mathematics, vol. 183 (Cambridge University Press, Cambridge, 2010).CrossRefGoogle Scholar
Deligne, P., Catégories tannakiennes, in The Grothendieck festschrift, Vol. II, Progress in Mathematics, vol. 87 (Birkhäuser, Boston, MA, 1990), 111–195.CrossRefGoogle Scholar
Drinfeld, V. G. and Simpson, C., B-structures on G-bundles and local triviality, Math. Res. Lett. 2 (1995), 823–829.CrossRefGoogle Scholar
Fargues, L., Quelques résultats et conjectures concernant la courbe, Astérisque 369 (2015), 325–374.Google Scholar
Fargues, L., Geometrization of the local langlands correspondence: an overview, Preprint (2016), arXiv:1602.00999.Google Scholar
Fargues, L. and Fontaine, J.-M., Factorization of analytic functions in mixed characteristic, in Frontiers of mathematical sciences (International Press, Somerville, MA, 2011), 307–315.Google Scholar
Fargues, L. and Fontaine, J. M., Vector bundles and p-adic Galois representations, in Fifth international congress of Chinese mathematicians, Part 1, AMS/IP Studies in Advanced Mathematics, vol. 51, part 1 (American Mathematical Society, Providence, RI, 2012), 77–113.Google Scholar
Fargues, L. and Fontaine, J.-M., Vector bundles on curves and p-adic hodge theory, in Automorphic forms and Galois representations, London Mathematical Society Lecture Note Series, vol. 415 (Cambridge University Press, Cambridge, 2014).Google Scholar
Fargues, L. and Fontaine, J.-M., Courbes et fibrés vectoriels en théorie de Hodge $p$-adique, Astérisque 406 (2018).Google Scholar
Fargues, L. and Scholze, P., Geometrization of the local Langlands correspondence, in preparation.Google Scholar
Fujiwara, K., A proof of the absolute purity conjecture (after Gabber), in Algebraic geometry 2000, Azumino (Hotaka), Advanced Studies in Pure Mathematics, vol. 36 (Mathematical Society of Japan, Tokyo, 2002), 153–183.Google Scholar
Grayson, D. R., Reduction theory using semistability. II, Comment. Math. Helv. 61 (1986), 661–676.CrossRefGoogle Scholar
Grothendieck, A., Torsion homologique et sections rationnelles, Séminaire Claude Chevalley 3 (1958), 5-01–5-29.Google Scholar
Grothendieck, A., Éléments de géométrie algébrique. IV. Étude locale des schémas et des morphismes de schémas IV, Publ. Math. Inst. Hautes Études Sci. 32 (1967), 361.Google Scholar
Grothendieck, A., Le groupe de Brauer: II. Théorie cohomologique, in Dix exposés sur la cohomologie des schémas (North-Holland, Amsterdam, 1968), 67–87.Google Scholar
Harder, G. and Narasimhan, M. S., On the cohomology groups of moduli spaces of vector bundles on curves, Math. Ann. 212 (1974/75), 215–248.CrossRefGoogle Scholar
Illusie, L. and Zheng, W., Quotient stacks and equivariant étale cohomology algebras: Quillen's theory revisited, J. Algebraic Geom. 25 (2016), 289–400.CrossRefGoogle Scholar
Kedlaya, K., Noetherian properties of Fargues-Fontaine curves, Preprint (2014), arXiv:1410.5160 [math.NT].CrossRefGoogle Scholar
Kottwitz, R. E., Isocrystals with additional structure, Compos. Math. 56 (1985), 201–220.Google Scholar
Kottwitz, R. E., Isocrystals with additional structure. II, Compos. Math. 109 (1997), 255–339.CrossRefGoogle Scholar
Labesse, J.-P., Cohomologie, stabilisation et changement de base, Astérisque 257 (1999).Google Scholar
Lang, S., The theory of real places, Ann. of Math. (2) 57 (1953), 378–391.CrossRefGoogle Scholar
Rapoport, M. and Richartz, M., On the classification and specialization of F-isocrystals with additional structure, Compos. Math. 103 (1996), 153–181.Google Scholar
Saavedra Rivano, N., Catégories Tannakiennes, Lecture Notes in Mathematics, vol. 265 (Springer, New York, NY, 1972).CrossRefGoogle Scholar
Serre, J.-P., Corps locaux, second edition, Publications de l'Université de Nancago, vol. 8 (Hermann, Paris, 1968).Google Scholar
Serre, J.-P., Cohomologie galoisienne, fifth edition, Lecture Notes in Mathematics, vol. 5 (Springer, Berlin, 1994).CrossRefGoogle Scholar
Gille, P. and Polo, P. (eds), Schémas en groupes (SGA 3), Tome III, Structure des schémas en groupes réductifs, Séminaire de Géométrie Algébrique du Bois Marie 1962–64 [Algebraic Geometry Seminar of Bois Marie 1962–64], a seminar directed by M. Demazure and A. Grothendieck with the collaboration of M. Artin, J.-E. Bertin, P. Gabriel, M. Raynaud and J.-P. Serre, Documents Mathématiques (Paris) [Mathematical Documents (Paris)], vol. 8 (Société Mathématique de France, Paris, 2011); revised and annotated edition of the 1970 French original.Google Scholar
Totaro, B., The torsion index of the spin groups, Duke Math. J. 129 (2005), 249–290.CrossRefGoogle Scholar
Ziegler, P., Graded and filtered fiber functors on Tannakian categories, J. Inst. Math. Jussieu 14 (2015), 87–130.CrossRefGoogle Scholar