Hostname: page-component-745bb68f8f-hvd4g Total loading time: 0 Render date: 2025-01-11T03:40:12.023Z Has data issue: false hasContentIssue false
  • English
  • Français

A Generalized Torelli Theorem

Published online by Cambridge University Press:  20 November 2018

Ajneet Dhillon
Ajneet Dhillon*
Affiliation:
Purdue University, email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Given a smooth projective curve 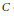$C$ of positive genus 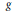$g$, Torelli's theorem asserts that the pair 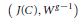$\left( J\left( C \right),\,{{W}^{g-1}} \right)$ determines 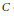$C$. We show that the theorem is true with 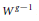${{W}^{g-1}}$ replaced by 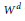${{W}^{d}}$ for each 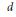$d$ in the range 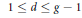$1\,\le \,d\,\le \,g\,-\,1$.

Keywords

14H99
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 55 , Issue 2 , 01 April 2003 , pp. 248 - 265
Copyright
Copyright © Canadian Mathematical Society 2003

References

[1] Andreotti, A., On a Theorem of Torelli. Amer J. Math. 80 (1958), 801–828.Google Scholar
[2] Arbarello, E., Cornalba, M., Griffiths, P. A. and Harris, J., Geometry of Algebraic Curves Volume 1. Springer Verlag, 1984.Google Scholar
[3] Fritzsche, K. and Grauert, H., Several Complex Variables. Springer Verlag, 1976.Google Scholar
[4] Griffiths, P. A. and Harris, J., Principles of Algebraic Geometry. John Wiley & Sons, 1978.Google Scholar
[5] Harris, J., Algebraic Geometry. A First Course. Graduate Texts in Math. 133, Springer Verlag, 1992.Google Scholar
[6] Hartshorne, R., Algebraic Geometry. Graduate Texts in Math. 52 Springer Verlag, 1977.Google Scholar
[7] Martens, H., An Extended Torelli Theorem. Amer. J. Math 87 (1965), 257–261.Google Scholar
[8] Ran, Z., On a Theorem of Martens. Rend. Sem. Mat. Univ. Politec. Torino (2) 44 (1986), 287–291.Google Scholar