Let $X$ be a smooth projective geometrically connected curve over a finite field with function field $K$. Let $g$ be a connected semisimple group scheme over $X$. Under certain hypotheses we prove the equality of two numbers associated with $g$. The first is an arithmetic invariant, its Tamagawa number. The second is a geometric invariant, the number of connected components of the moduli stack of $g$-torsors on $X$. Our results are most useful for studying connected components as much is known about Tamagawa numbers.

Let $R$ be a homomorphic image of a Gorenstein local ring. Recent work has shown that there is a bridge between Auslander categories and modules of finite Gorenstein homological dimensions over $R$.

We use Gorenstein dimensions to prove new results about Auslander categories and vice versa. For example, we establish base change relations between the Auslander categories of the source and target rings of a homomorphism 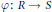$\varphi :\,R\,\to \,S$ of finite flat dimension.

We compute some Hodge and Betti numbers of the moduli space of stable rank $r$, degree $d$ vector bundles on a smooth projective curve. We do not assume $r$ and $d$ are coprime. In the process we equip the cohomology of an arbitrary algebraic stack with a functorial mixed Hodge structure. This Hodge structure is computed in the case of the moduli stack of rank $r$, degree $d$ vector bundles on a curve. Our methods also yield a formula for the Poincaré polynomial of the moduli stack that is valid over any ground field. In the last section we use the previous sections to give a proof that the Tamagawa number of $\text{S}{{\text{L}}_{n}}$ is one.