Hostname: page-component-669899f699-cf6xr Total loading time: 0 Render date: 2025-04-25T22:01:08.362Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Cohomology of Moduli of Vector Bundles and the Tamagawa Number of SLn

Published online by Cambridge University Press:  20 November 2018

Ajneet Dhillon
Ajneet Dhillon*
Affiliation:
Department of Mathematics, University of Western Ontario, London, ON N6A 3K7 e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We compute some Hodge and Betti numbers of the moduli space of stable rank 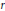$r$, degree 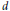$d$ vector bundles on a smooth projective curve. We do not assume 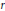$r$ and 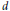$d$ are coprime. In the process we equip the cohomology of an arbitrary algebraic stack with a functorial mixed Hodge structure. This Hodge structure is computed in the case of the moduli stack of rank 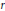$r$, degree 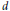$d$ vector bundles on a curve. Our methods also yield a formula for the Poincaré polynomial of the moduli stack that is valid over any ground field. In the last section we use the previous sections to give a proof that the Tamagawa number of 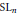$\text{S}{{\text{L}}_{n}}$ is one.

Keywords

14H14L
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 58 , Issue 5 , 01 October 2006 , pp. 1000 - 1025
Copyright
Copyright © Canadian Mathematical Society 2006

References

[AB82] Atiyah, M. and Bott, R., The Yang-Mills equations over Riemann surfaces. Philos. Trans. Roy. Soc. London Ser. A 308(1982), no. 1505, 523–615.Google Scholar
[AS01] Arapura, D. and Sastry, P., Intermediate Jacobians and Hodge structures of moduli spaces. Proc. Indian Acad. Sci. Math. Sci. 110(2001), 1–26.Google Scholar
[Bal93] Balaji, V., On the cohomology of a moduli space of vector bundles on curves. In: Proceedings of the Indo-French Conference on Geometry. Hindustan Book Agency, Mumbai, 1993, pp. 1–11.Google Scholar
[Bal90] Balaji, V. and Seshadri, C. S., Cohomology of a moduli space of vector bundles. In: The Grothendieck Festschrift, Vol. I. Birkhäuser, Boston, 1990, pp. 87–120.Google Scholar
[BKN97] Balaji, V., King, A., and Newstead, P., Algebraic cohomology of the moduli space of ran. 2 vector bundles on a curve. Topology 36(1997), no. 2, 567–577.Google Scholar
[Beh] Behrend, K., The Lefschetz trace formula for the moduli stack of principal bundles. Ph. D. dissertation, University of California, Berkeley, 1991. Available at http://www.math.ubc.ca/behrend/thesis.html. Google Scholar
[Beh93] Behrend, K., The Lefschetz trace formula for algebraic stacks. Invent.Math. 112(1993), no. 1, 127–149.Google Scholar
[Beh02] Behrend, K., Cohomology of quotient stacks and DM stacks. http://www.msri.org. Google Scholar
[Beh03] Behrend, K., Derived ℓ-adic categories for algebraic stacks. Mem. Amer. Math. Soc. 163, American Mathematical Society, Providence, RI, 2003.Google Scholar
[Beh06] Behrend, K. and Dhillon, A., Connected components of module stacks of torsors via Tamagawa numbers. arXiv:math.NT/0503383.Google Scholar
[BB73] Białynicki-Birula, A., Some theorems on the actions of algebraic groups. Ann. of Math. 98(1973), 480–497.Google Scholar
[BB74] Białynicki-Birula, A., On fixed points of torus actions on projective varieties. Bull. Acad. Polon. Sér. Sci. Math. Astronom. Phys. 22(1974), 1097–1101.Google Scholar
[Bif89] Bifet, E., Sur les points fixes du schém Quot sous l’action du tore Gr m,k. C. R. Acad. Sci. Paris Sér.Math. 309(1989), 609–612.Google Scholar
[BGL94] Bifet, E., Ghione, F., and Letizia, M., On the Abel-Jacobi map for divisors of higher rank on a curve. Math. Ann. 299(1994), no. 4, 641–672.Google Scholar
[Bru83] Bruguieres, A., Filtration de Harder-Narasimhan et stratification. In: Module des fibres stable sur les courbes algébriques. Birkhäuser, Boston, 1983, pp. 81–104.Google Scholar
[dB01] del Baño, S., On the Chow motive of some moduli spaces. J. Reine Angew. Math. 532(2001), 105–132.Google Scholar
[Del71] Deligne, P., Théorie de Hodge. II. Inst. Hautes Études Sci. Publ. Math. 40(1971), 5–57.Google Scholar
[Del74] Deligne, P., Théorie de Hodge. III. Inst. Hautes Études Sci. Publ. Math. 44(1974), 5–77.Google Scholar
[Ful98] Fulton, W., Intersection Theory. Second edition. Ergebnisse derMathematik und ihrer Grenzgebiete 2, Springer-Verlag, Berlin, 1998.Google Scholar
[Gom] Gomez, T., Algebraic stacks. http://arxiv.org/math.AG/9911199v1 Google Scholar
[HN75] Harder, G. and Narasimhan, M. S, On the cohomology of moduli spaces of vector bundles on curves. Math. Ann. 212(1974/75), 212–248.Google Scholar
[Hir64] Hironaka, H., Resolution of singularities of an algebraic variety over a field of characteristic zero. I. Ann.Math. 79(1964), 109–326.Google Scholar
[LMB00] Laumon, G. and Moret-Bailly, L., Champs algébriques. Ergebnisse der Mathematik und ihrer Grenzgebiete 39, Springer-Verlag, Berlin, 2000.Google Scholar
[Mil80] Milne, J. S., Étale cohomology. Princeton Mathematical Series 33, Princeton University Press, Princeton, NJ, 1980.Google Scholar
[Nag62] Nagata, M., Imbedding of an abstract variety in a complete variety. J. Math. Kyoto Univ. 2(1962), 1–10.Google Scholar
[Oes84] Oesterlé, J., Nombre de Tamagawa et groupes unipotents en caractéristique p. Invent. Math. 78(1984), 13–88.Google Scholar
[Pot97] Le Potier, J., Lectures on Vector Bundles. Cambridge Studeis in Advanced Mathematics 54, Cambridge University Press, 1997.Google Scholar
[SD72] Saint-Donat, B., Techniques de descente cohomologique. In: Théorie des Topos et Cohomologie Etale des Schémas, Lecture Notes in Mathematics 270, Springer-Verlag, Berlin, 1972, pp. 83–162.Google Scholar
[Tel98] Teleman, C., Borel-Weil-Bott theory on the moduli stack of G-bundles over a curve. Invent. Math. 134(1998), no. 1, 1–57.Google Scholar
[Wei82] Weil, A., Adeles and Algebraic Groups. Progress in Mathematics 23, Birkhauser, Boston, 1982.Google Scholar