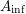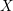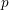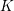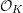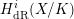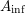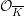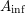4 results
The
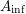 $A_{\text{inf}}$-cohomology in the semistable case
$A_{\text{inf}}$-cohomology in the semistable case
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 11 / November 2019
- Published online by Cambridge University Press:
- 09 September 2019, pp. 2039-2128
- Print publication:
- November 2019
-
- Article
- Export citation
Semistable reduction for overconvergent F-isocrystals, IV: local semistable reduction at nonmonomial valuations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 2 / March 2011
- Published online by Cambridge University Press:
- 21 February 2011, pp. 467-523
- Print publication:
- March 2011
-
- Article
-
- You have access
- Export citation
Semistable reduction for overconvergent F-isocrystals, III: Local semistable reduction at monomial valuations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 1 / January 2009
- Published online by Cambridge University Press:
- 01 January 2009, pp. 143-172
- Print publication:
- January 2009
-
- Article
-
- You have access
- Export citation
Semistable reduction for overconvergent $F$-isocrystals I: Unipotence and logarithmic extensions
-
- Journal:
- Compositio Mathematica / Volume 143 / Issue 5 / September 2007
- Published online by Cambridge University Press:
- 20 September 2007, pp. 1164-1212
- Print publication:
- September 2007
-
- Article
-
- You have access
- Export citation