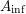Hostname: page-component-6bf8c574d5-vmclg Total loading time: 0 Render date: 2025-02-19T20:28:42.783Z Has data issue: false hasContentIssue false
  • English
  • Français

The $A_{\text{inf}}$-cohomology in the semistable case

Part of: (Co)homology theory Arithmetic problems. Diophantine geometry

Published online by Cambridge University Press:  09 September 2019

Kęstutis Česnavičius  and
Teruhisa Koshikawa
Kęstutis Česnavičius
Affiliation:
CNRS, UMR 8628, Laboratoire de Mathématiques d’Orsay, Univ. Paris-Sud, Université Paris-Saclay, 91405 Orsay, France email [email protected]
Teruhisa Koshikawa
Affiliation:
Research Institute for Mathematical Sciences, Kyoto University, Kyoto 606-8502, Japan email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For a proper, smooth scheme 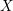$X$ over a 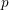$p$-adic field 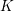$K$, we show that any proper, flat, semistable 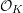${\mathcal{O}}_{K}$-model 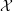${\mathcal{X}}$ of 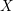$X$ whose logarithmic de Rham cohomology is torsion free determines the same 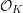${\mathcal{O}}_{K}$-lattice inside 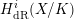$H_{\text{dR}}^{i}(X/K)$ and, moreover, that this lattice is functorial in 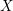$X$. For this, we extend the results of Bhatt–Morrow–Scholze on the construction and the analysis of an 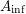$A_{\text{inf}}$-valued cohomology theory of 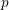$p$-adic formal, proper, smooth 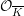${\mathcal{O}}_{\overline{K}}$-schemes 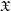$\mathfrak{X}$ to the semistable case. The relation of the 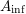$A_{\text{inf}}$-cohomology to the 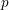$p$-adic étale and the logarithmic crystalline cohomologies allows us to reprove the semistable conjecture of Fontaine–Jannsen.

Keywords

comparison isomorphismintegral cohomologyp-adic Hodge theory

MSC classification

Primary: 14G20: Local ground fields
Secondary: 14G22: Rigid analytic geometry 14F20: Étale and other Grothendieck topologies and (co)homologies 14F30: $p$-adic cohomology, crystalline cohomology 14F40: de Rham cohomology
Type
Research Article
Information
Compositio Mathematica , Volume 155 , Issue 11 , November 2019 , pp. 2039 - 2128
Copyright
© The Authors 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Beilinson, A. A., Bernstein, J. and Deligne, P., Faisceaux pervers , in Analysis and topology on singular spaces, I (Luminy, 1981), Astérisque, vol. 100 (Société Mathématique de France, Paris, 1982), 5–171 (French); MR 751966 (86g:32015).Google Scholar
Brinon, O. and Conrad, B., CMI summer school notes on $p$ -adic Hodge theory. Available at http://math.stanford.edu/∼conrad/papers/notes.pdf, version of June 24, 2009.Google Scholar
Beilinson, A., p-adic periods and derived de Rham cohomology , J. Amer. Math. Soc. 25 (2012), 715–738, doi:10.1090/S0894-0347-2012-00729-2; MR 2904571.Google Scholar
Beilinson, A., On the crystalline period map , Camb. J. Math. 1 (2013), 1–51; MR 3272051.Google Scholar
Beilinson, A., On the crystalline period map, Preprint (2013), arXiv:1111.3316v4.Google Scholar
Bhatt, B., $p$ -adic derived de Rham cohomology, Preprint (2012), arXiv:1204.6560.Google Scholar
Bhatt, B., Specializing varieties and their cohomology from characteristic 0 to characteristic p , in Algebraic geometry: Salt Lake City 2015, Proceedings of Symposia in Pure Mathematics, vol. 97 (American Mathematical Society, Providence, RI, 2018), 43–88; MR 3821167.Google Scholar
Bosch, S., Lütkebohmert, W. and Raynaud, M., Néron models , Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)], vol. 21 (Springer, Berlin, 1990); MR 1045822 (91i:14034).Google Scholar
Bhatt, B., Morrow, M. and Scholze, P., Integral $p$ -adic Hodge theory, Preprint (2018) arXiv:1602.03148.Google Scholar
Bourbaki, N., Éléments de mathématique. Algèbre commutative, ch. I-VII (Hermann, 1961, 1964, 1965); ch. VIII-X (Springer, 2006, 2007) (French).Google Scholar
Brinon, O., Représentations cristallines dans le cas d’un corps résiduel imparfait , Ann. Inst. Fourier (Grenoble) 56 (2006), 919–999 (French, with English and French summaries); MR 2266883.Google Scholar
Bhatt, B. and Scholze, P., The pro-étale topology for schemes , Astérisque 369 (2015), 99–201 (English, with English and French summaries); MR 3379634.Google Scholar
Colmez, P. and Nizioł, W., Syntomic complexes and p-adic nearby cycles , Invent. Math. 208 (2017), 1–108; MR 3621832.Google Scholar
Conrad, B., Irreducible components of rigid spaces , Ann. Inst. Fourier (Grenoble) 49 (1999), 473–541 (English, with English and French summaries); MR 1697371.Google Scholar
Grothendieck, A. and Dieudonné, J., Éléments de géométrie algébrique. I. Le langage des schémas , Inst. Hautes Études Sci. Publ. Math. 4 (1960), 228; MR 0217083 (36 #177a).Google Scholar
Grothendieck, A. and Dieudonné, J., Éléments de géométrie algébrique. III. Étude cohomologique des faisceaux cohérents. I , Inst. Hautes Études Sci. Publ. Math. 11 (1961), 167; MR 0217085 (36 #177c).Google Scholar
Grothendieck, A. and Dieudonné, J., Éléments de géométrie algébrique. IV. Étude locale des schémas et des morphismes de schémas. II , Inst. Hautes Études Sci. Publ. Math. 24 (1965), 231 (French); MR 0199181 (33 #7330).Google Scholar
Faltings, G., Almost étale extensions , in Cohomologies p-adiques et applications arithmétiques, II, Astérisque, vol. 279 (Société Mathématique de France, Paris, 2002), 185–270; MR 1922831.Google Scholar
Fujiwara, K. and Kato, F., Foundations of rigid geometry. I, EMS Monographs in Mathematics (European Mathematical Society, Zürich, 2018); MR 3752648.Google Scholar
Fontaine, J.-M., Formes différentielles et modules de Tate des variétés abéliennes sur les corps locaux , Invent. Math. 65 (1982), 379–409 (French); MR 643559.Google Scholar
Fontaine, J.-M., Le corps des periodes p-adiques. With an appendix by Pierre Colmez , in Périodes p-adiques (Bures-sur-Yvette, 1988), Astérisque, vol. 223 (Société Mathématique de France, Paris, 1994), 59–111 (French); MR 1293971.Google Scholar
Gabber, O. and Ramero, L., Almost ring theory , Lecture Notes in Mathematics, vol. 1800 (Springer, Berlin, 2003); MR 2004652.Google Scholar
Huber, R., Continuous valuations , Math. Z. 212 (1993), 455–477; MR 1207303.Google Scholar
Huber, R., A generalization of formal schemes and rigid analytic varieties , Math. Z. 217 (1994), 513–551; MR 1306024.Google Scholar
Huber, R., Étale cohomology of rigid analytic varieties and adic spaces , Aspects of Mathematics, E30 (Friedr. Vieweg & Sohn, Braunschweig, 1996); MR 1734903.Google Scholar
Illusie, L., Complexe cotangent et déformations. I , Lecture Notes in Mathematics, vol. 239 (Springer, Berlin–New York, 1971) (French); MR 0491680.Google Scholar
Kato, K., Logarithmic structures of Fontaine–Illusie , in Algebraic analysis, geometry, and number theory (Baltimore, MD, 1988) (Johns Hopkins University Press, Baltimore, MD, 1989), 191–224; MR 1463703 (99b:14020).Google Scholar
Kato, K., Semi-stable reduction and p-adic étale cohomology , in Périodes p-adiques (Bures-sur-Yvette, 1988), Astérisque, vol. 223 (Société Mathématique de France, Paris, 1994), 269–293; MR 1293975.Google Scholar
Kato, K., Toric singularities , Amer. J. Math. 116 (1994), 1073–1099; MR 1296725.Google Scholar
Liu, T., Compatibility of Kisin modules for different uniformizers , J. reine angew. 740 (2018), 1–24.Google Scholar
Morrow, M., Notes on the  $\mathbb{A}_{\text{inf}}$ -cohomology of integral  $p$ -adic Hodge theory, Preprint (2016), arXiv:1608.00922.Google Scholar
Nizioł, W., Semistable conjecture via K-theory , Duke Math. J. 141 (2008), 151–178; MR 2372150.Google Scholar
Ogus, A., Lectures on Logarithmic Algebraic Geometry, Cambridge Studies in Advanced Mathematics, vol. 178 (Cambridge University Press, 2018).Google Scholar
Raynaud, M. and Gruson, L., Critères de platitude et de projectivité. Techniques de ‘platification’ d’un module , Invent. Math. 13 (1971), 1–89 (French); MR 0308104.Google Scholar
Scholze, P., Perfectoid spaces , Publ. Math. Inst. Hautes Études Sci. 116 (2012), 245–313; MR 3090258.Google Scholar
Scholze, P., p-adic Hodge theory for rigid-analytic varieties , Forum Math. Pi 1 (2013), e1, 77; MR 3090230.Google Scholar
Scholze, P., Perfectoid spaces: a survey , in Current developments in mathematics 2012 (Int. Press, Somerville, MA, 2013), 193–227; MR 3204346.Google Scholar
Scholze, P., p-adic Hodge theory for rigid-analytic varieties—corrigendum [MR3090230] , Forum Math. Pi 4 (2016), e6, 4; MR 3535697.Google Scholar
Artin, M., Grothendieck, A. and Verdier, J. L. (eds), Séminaire de Géométrie Algébrique du Bois Marie – 1963–64 – Théorie des topos et cohomologie étale des schémas (SGA 4), tome 2, Lecture Notes in Mathematics, vol. 270 (Springer, Berlin, 1972), avec la collaboration de N. Bourbaki, P. Deligne et B. Saint-Donat (in French); MR 0354653 (50 #7131).Google Scholar
Grothendieck, A., Séminaire de Géométrie Algébrique du Bois Marie – 1967–69 – Groupes de monodromie en géométrie algébrique (SGA 7), vol. 1, Lecture Notes in Mathematics, vol. 288 (Springer, Berlin, 1972), avec la collaboration de M. Raynaud et D. S. Rim (in French); MR 0354656 (50 #7134).Google Scholar
The Stacks Project Authors, Stacks Project, https://stacks.math.columbia.edu, 2018.Google Scholar
Szamuely, T. and Zábrádi, G., The p-adic Hodge decomposition according to Beilinson , in Algebraic geometry: Salt Lake City 2015, Proceedings of Symposia in Pure Mathematics, vol. 97 (American Mathematical Society, Providence, RI, 2018), 495–572; MR 3821183.Google Scholar
Tsuji, T., p-adic étale cohomology and crystalline cohomology in the semi-stable reduction case , Invent. Math. 137 (1999), 233–411; MR 1705837.Google Scholar
Tan, F. and Tong, J., Crystalline comparison isomorphisms in  $p$ -adic Hodge theory: the absolutely unramified case, Preprint (2015), arXiv:1510.05543.Google Scholar
Ullrich, P., The direct image theorem in formal and rigid geometry , Math. Ann. 301 (1995), 69–104; MR 1312570.Google Scholar