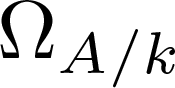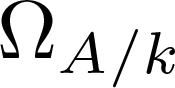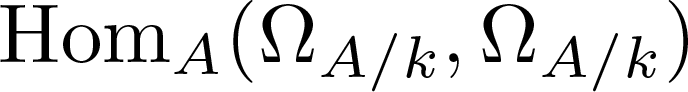4 results
On one-dimensional local rings and Berger’s conjecture
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 23 May 2023, pp. 437-452
-
- Article
- Export citation
Bertini theorem for normality on local rings in mixed characteristic (applications to characteristic ideals)
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 218 / June 2015
- Published online by Cambridge University Press:
- 11 January 2016, pp. 125-173
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
Symplectic Lie–Rinehart–Jacobi Algebras and Contact Manifolds
-
- Journal:
- Canadian Mathematical Bulletin / Volume 54 / Issue 4 / 01 December 2011
- Published online by Cambridge University Press:
- 20 November 2018, pp. 716-725
- Print publication:
- 01 December 2011
-
- Article
-
- You have access
- Export citation
Differential Completions and Differentially Simple Algebras
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 32 / Issue 3 / 01 September 1989
- Published online by Cambridge University Press:
- 20 November 2018, pp. 314-319
- Print publication:
- 01 September 1989
-
- Article
-
- You have access
- Export citation