Published online by Cambridge University Press: 23 May 2023
Let k be a field of characteristic zero and let 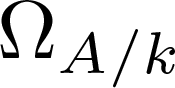 $\Omega_{A/k}$ be the universally finite differential module of a k-algebra A, which is the local ring of a closed point of an algebraic or algebroid curve over k. A notorious open problem, known as Berger’s Conjecture, predicts that A must be regular if
$\Omega_{A/k}$ be the universally finite differential module of a k-algebra A, which is the local ring of a closed point of an algebraic or algebroid curve over k. A notorious open problem, known as Berger’s Conjecture, predicts that A must be regular if 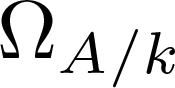 $\Omega_{A/k}$ is torsion-free. In this paper, assuming the hypotheses of the conjecture and observing that the module
$\Omega_{A/k}$ is torsion-free. In this paper, assuming the hypotheses of the conjecture and observing that the module 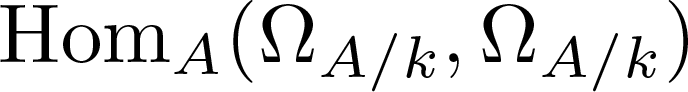 ${\rm Hom}_A(\Omega_{A/k}, \Omega_{A/k})$ is then isomorphic to an ideal of A, say
${\rm Hom}_A(\Omega_{A/k}, \Omega_{A/k})$ is then isomorphic to an ideal of A, say 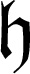 $\mathfrak{h}$, we show that A is regular whenever the ring
$\mathfrak{h}$, we show that A is regular whenever the ring 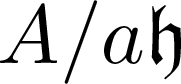 $A/a\mathfrak{h}$ is Gorenstein for some parameter a (and conversely). In addition, we provide various characterizations for the regularity of A in the context of the conjecture.
$A/a\mathfrak{h}$ is Gorenstein for some parameter a (and conversely). In addition, we provide various characterizations for the regularity of A in the context of the conjecture.