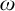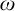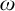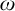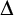5 results
INVARIANT KEISLER MEASURES FOR
 $\omega $-CATEGORICAL STRUCTURES
$\omega $-CATEGORICAL STRUCTURES
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 22 May 2024, pp. 1-17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ELIMINATION OF IMAGINARIES IN ORDERED ABELIAN GROUPS WITH BOUNDED REGULAR RANK
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 06 February 2023, pp. 1639-1654
- Print publication:
- December 2023
-
- Article
- Export citation
APPROXIMATING TREES AS COLOURED LINEAR ORDERS AND COMPLETE AXIOMATISATIONS OF SOME CLASSES OF TREES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 08 June 2021, pp. 1035-1065
- Print publication:
- September 2021
-
- Article
- Export citation
CHARACTERIZING O-MINIMAL GROUPS IN TAME EXPANSIONS OF O-MINIMAL STRUCTURES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 2 / March 2021
- Published online by Cambridge University Press:
- 16 July 2019, pp. 699-724
- Print publication:
- March 2021
-
- Article
-
- You have access
- Open access
- Export citation
Non-standard lattices and o-minimal groups
-
- Journal:
- Bulletin of Symbolic Logic / Volume 19 / Issue 1 / March 2013
- Published online by Cambridge University Press:
- 05 September 2014, pp. 56-76
- Print publication:
- March 2013
-
- Article
- Export citation